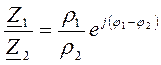(Лаб. раб.№2, стр.3-6)
Известно пара способов представления размеров, изменяющихся по синусоидальному закону: в виде
1) тригонометрических функций,
2) графиков трансформаций функций во времени,
3) вращающихся векторов,
4) комплексных чисел
Представление синусоидальных размеров вращающимися векторами
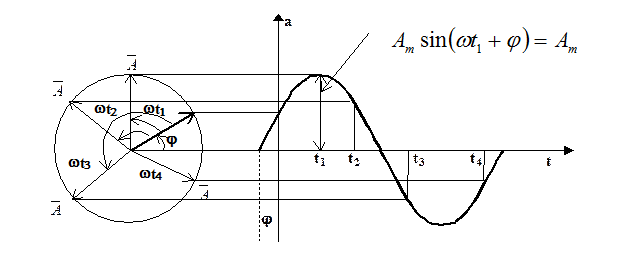
Для представления синусоидально изменяющейся величины
с начальной фазой вращающимся вектором выстроим радиус-вектор данной величины длиной равной амплитуде и под углом к горизонтальной оси. Это будет его исходное состояние в момент начала отсчета времени . Проекция этого вектора на вертикальную ось равна .
Предположим, что радиус-вектор вращается с постоянной угловой скоростью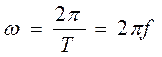 
против направления перемещения часовой стрелки.
В произвольный момент времени радиус вектор будет повернут довольно начального на угол ; проекция его на ось ординат равна .
Рядом с окружностью, обрисовываемой финишем вращающегося радиус вектора, возможно выстроить в прямоугольной совокупности координат график синусоидальной величины от фазы либо от времени .
Использование вращающихся векторов разрешает компактно представить на одном рисунке совокупность разных синусоидально изменяющихся размеров однообразной частоты при анализе сложной электрической цепи.
Использование комплексных чисел для расчета электрических цепей синусоидального тока
Главная часть электрооборудования трудится на переменном токе. Исходя из этого серьёзным вопросом электротехники есть расчет электрических цепей синусоидального тока. Решить эту задачу грамотно запрещено, не зная комплексного способа расчета.
Число (1) именуется комплексным числом. Тут а – настоящая, а в – мнимая часть числа, .
Комплексные числа не являются числами в элементарном смысле этого слова, а являются математические объекты, наделенные определенными особенностями.
В случае, если настоящие числа возможно изображать точками числовой прямой, то комплексные числа возможно изображать точками плоскости.
Плоскость, точки которой изображают комплексные числа, именуется комплексной плоскостью.
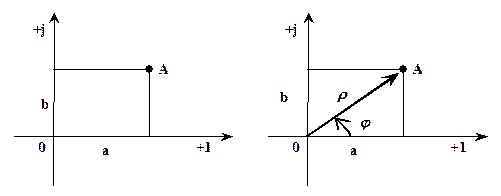
Кроме представления комплексного числа в декартовых координатах его возможно задавать полярной совокупностью координат. Совместив полюс полярной совокупностью координат с точкой 0, возможно любую изображающую точку плоскости (соответственно, любое комплексное число) изображать радиус-фазой и вектором (полярным углом). Угол отсчитывается от настоящей оси, причем в случае, если вращение радиус-вектора происходит против часовой стрелки, то , в случае, если по часовой стрелке, то .
Протяженность радиус-вектора есть модулем комплексного числа.
Комплексное число может изображаться и в показательной форме
(2)
где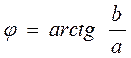 
есть оператором поворота и показывает на то, что радиус-вектор развёрнут на угол довольно настоящей оси.
Высказывая координаты а и в как соответствующие проекции радиус-вектора на настоящую и мнимую оси, приобретаем тригонометрическую форму записи комплексного числа
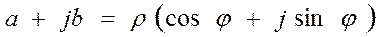
либо (3)
Последнее выражение именуется формулой Эйлера и имеет крайне важное значение при расчете цепей синусоидального тока комплексным способом.
Главные арифметические действия над комплексными числами: ;
1) Сложение
2) Вычитание
3) Умножение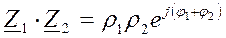 
4) Деление 