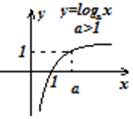Схема построения графиков
Имеется пара способов задавать зависимость между переменными и . Значительно чаще употребляется явное выражение . Можно считать и функциями от параметра: . Возможно задать эту зависимость в виде уравнения
. В последнем случае говорят о неявно заданной функции.
Графическое изображение функциональной зависимости разрешает наглядно представить свойства изучаемой функции.
Обрисуем схему построения графика функции, заданного явным уравнением . Отметим, что график данной функции является множеством точек на плоскости, координаты которых связаны равенством .
При изучении функции направляться затевать с нахождения области определения данной функции. В большинстве случаев, в то время, когда ставится задача выстроить график функции , рассматривается естественная область определения, т.е. множество чисел , при которых выяснено выражение . Во многих случаях рассматривается часть области определения, обозначим эту часть . Тогда мы говорим об ограничении функции на множество .
Ограничения функции на разные подмножества и смогут владеть различными особенностями. К примеру, ограничение функции на множество
– убывающая функция, а ограничение – возрастающая функция.
По окончании нахождения области определения функции, исследуем её на непрерывность и выясняем её асимптотическое поведение при рвении к вечно удалённым точкам, либо к граничным точкам области определения.
Кое-какие функции владеют своеобразными особенностями. Отметим, что функция именуется чётной, если она выяснена на симметричном относительно точки множестве и в случае, если для любого выполняется равенство . График чётной функции симметричен относительно оси . Нечётной именуется функция , если она выяснена на симметричном относительно точки множестве и в случае, если для любого имеет место равенство . График нечётной функции симметричен относительно начала координат. Функция именуется периодической, в случае, если существует число такое, что для любого – области определения функции числа кроме этого принадлежат и .
Потом вычисляем производную и исследуем её символ. На множестве, где , функция возрастает, на множествах, где , функция убывает. Экстремумы функция может иметь в тех точках, где или , или не существует. Нахождение громаднейшего либо мельчайшего значений функции, если они имеется, разрешает установить множество значений, принимаемых функцией.
Изучение символа второй производной разрешает установить промежутки, на которых график функции выпукл вверх, либо выпукл вниз, и точки перегиба.
Преобразования графиков
Пускай выяснена на множестве , возрастает на (либо убывает на ) и пускай – множество значений данной функции. Тогда для любого существует единственное значение такое, что . Это обозначим так: . Обратной для функцией назовём функцию . Для всех выполнено равенство . Для всех выполнено равенство . К примеру для имеем: , . Исходя из этого для всех и для всех .
График обратной функции симметричен графику функции относительно биссектрисы координатного угла.
Термины “сложная функция”, либо “композиция функций” (и “суперпозиция функций”) относятся к методу представления функции. В случае, если, к примеру, и выяснена на множестве значений , принимаемых функцией , то говорят, что – сложная функция, либо композиция этих функций.
Особенно довольно часто рассматриваются сложные функции вида .
Так как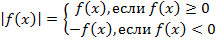 
, точки графика , для которых , в один момент являются и точками графика . Те точки графика , для которых , при построении графика заменяются точками , т.е. точками симметричными относительно оси .
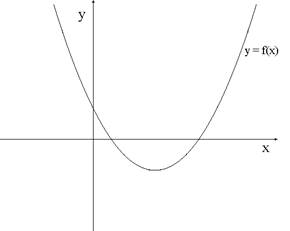
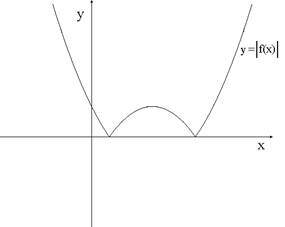
При построении графика функции сохраняем точки графика функции для которых , а позже соответствуют значения , т.е. график получается симметричным относительно оси отражением графика ограничения на множество функции .
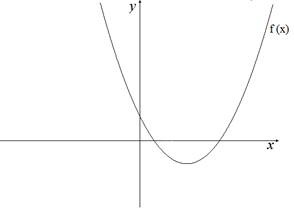
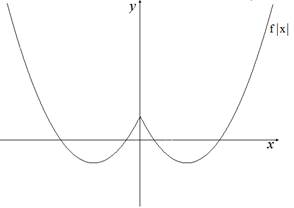
Перейдём к построению графиков вида и начнём с рассмотрения серьёзных частных случаев.
График функции получается из графика функции сдвигом на число по оси :
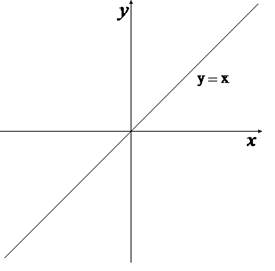
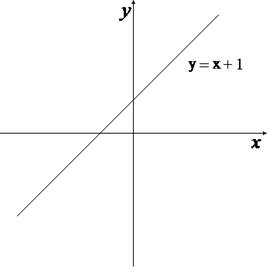
График функции получается из графика функции сдвигом на число по оси
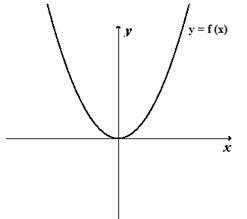
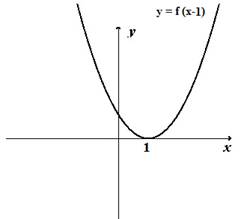
График функции получается из графика умножением координаты на число
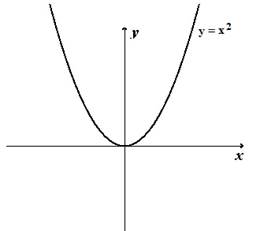
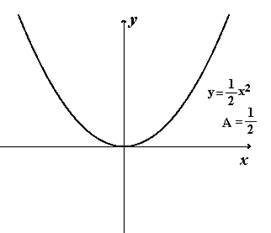
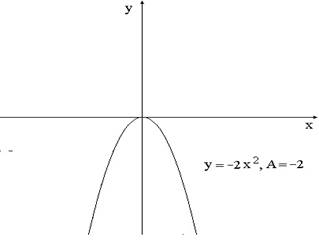
График получается из графика при сжатием на протяжении оси в раз, в случае, если и растяжением в раз, в случае, если .
В случае, если же , то для построения графика направляться выстроить график в соответствии с вышеуказанному правилу, после этого отразить полученный график симметрично относительно оси .
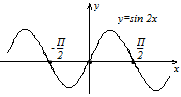
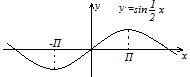
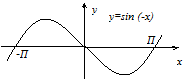
Для получения графика функции направляться представить её в виде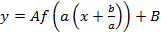 
и последовательно применять приведённые выше правила.
Графики главных элементарных функций
Элементарной именуется функция, которая возможно представлена в виде композиции нескольких главных арифметических операций и элементарных функций над ними. К главным элементарным функциям относятся степенные, показательные, логарифмические, тригонометрические и обратные тригонометрические функции. Эти функции употребляются в математических моделях.
3.1. Степенная функция
свойства и Область определения данной функции зависят от числа .
При график функции имеет форму:
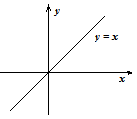
В случае, если , то по определению, , в случае, если . В точке эта функция неопределена. Отметим, что знак употребляется для обозначения так называемой неопределенности. График функции имеет форму:
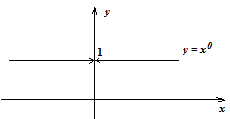
При всех функция выяснена по крайней мере на множестве (при некоторых естественной областью определения есть вся числовая прямая, см. ниже).
Эта функция постоянна на всех области определения, . Так как для всех , функция возрастает на области определения. Множеством ее значений есть множество .
Вторая производная равна .
Ее величина больше 0 для всех , в случае, если и меньше 0 для всех , в случае, если . В первом случае график выгнут вниз, во втором – вверх.
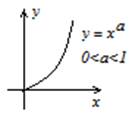
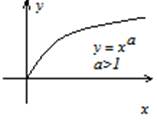
Возвратимся к вопросу о естественной области определения. В случае, если — натуральное число, или – рациональное число, которое возможно представить несократимой дробью , знаменатель которой — нечетное число, то естественной областью определения функции есть все множество ?. Наряду с этим, в случае, если — четное число, то — четная функция, ее график симметричен относительно оси и при имеет форму
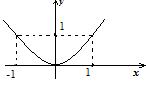
Наряду с этим в точке функция имеет минимум и везде выгнута вниз.
При график имеет форму
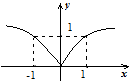
Функция имеет точку минимума в которой производной не существует и — вертикальная касательная к графику.
В случае, если – нечетное натуральное число, или , где – нечетные натуральные числа, то функция – нечетная, ее график симметричен относительно начала координат и при имеет форму
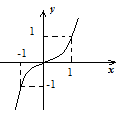
Функция возрастает на всей прямой, выгнута вверх при , выгнута вниз при , в точке имеется перегиб. Множество ее значений сходится с ?.
При график имеет форму
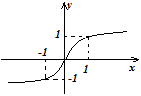
Функция кроме этого возрастает на всей прямой и множеством ее значений есть ?. Но она выгнута вниз при и выгнута вверх при . В точке имеется перегиб, не смотря на то, что функция не дифференцируема в данной точке и ее график в точке имеет вертикальную касательную.
В случае, если , то функция выяснена, по крайней мере на множестве (при некоторых естественной областью определения есть множество ).
Эта функция постоянна на области определения, . , исходя из этого график имеет горизонтальную и вертикальную асимптоту .
Производная для всех , исходя из этого функция убывает. Вторая производная для всех , исходя из этого график выгнут вниз. Ее график имеет форму
Опять разглядим вопрос о естественной области определения. В случае, если – отрицательное целое число либо рациональное число , где — натуральные числа, причем — нечетное число, то областью определения функции есть множество . Наряду с этим, в случае, если — четное число, или , где — четное число, то функция — четная.
График функции в этом случае имеет форму
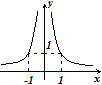
Функция возрастает при , убывает при . График везде выгнут вниз. Имеются горизонтальная и вертикальная асимптота .
Множеством значений есть .
В случае, если — нечетное число, или , где — нечетные натуральные числа, то — нечетная функция, и ее график имеет форму
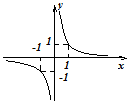
Она убывает на всей области определения, множество ее значений: множество . Помимо этого, функция выгнута вверх при , выгнута вниз при .
Показательная функция
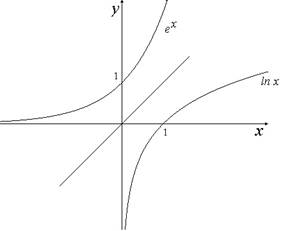
Показательная функция , выяснена при всех и принимает хорошие значения. Она постоянна на всей прямой. В случае, если , то , а вдруг , то . Её производная равна . Эта величина меньше для всех , в случае, если . Наряду с этим функция возрастает. В случае, если же , то производная для всех , функция убывает. Её вторая производная для всех и всех . Исходя из этого график выгнут вниз. На рисунке изображены графики при и , соответственно.
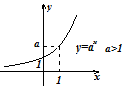
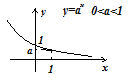
Логарифмическая функция
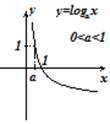
Логарифмическая функция есть обратной для показательной функции, т.е. для всех .
Областью определения логарифмической функции есть множество . Очевидно, показательная функция также есть обратной функцией для логарифмической, но лишь при .
Логарифмическая функция постоянна в собственной области определения.
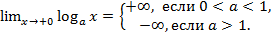
Исходя из этого ее график имеет вертикальную асимптоту . Производная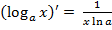 
хорошая при , в случае, если и отрицательна, в случае, если . Исходя из этого при функция возрастает, при убывает. Множество ее значений: . Вторая производная 
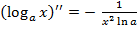отрицательна при и хороша, в случае, если . Исходя из этого в первом случае график выгнут вверх, а во втором случае – вниз. Очевидно, график данной функции симметричен графику соответствующей показательной функции относительно биссектрисы первого и третьего координатных углов.
