1.Упростить выражение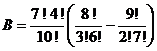 
.
Было бы неправильным все факториалы, по окончании чего перейти к математике ? через чур большие числа. Используем, где быть может, расчленение факториалов:
; 
;
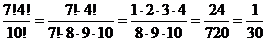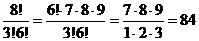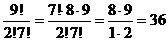. Следовательно, 
.
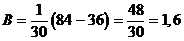2.Упростить выражение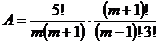 
Отметим, что ;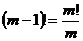 
и , тогда
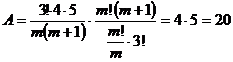
3..При расследовании кражи установлено, что у преступника семизначный телефонный номер, в котором ни одна цифра не повторяется. Следователь, полагая, что перебор этих номеров потребует одного-двух часов, рассказал о раскрытии правонарушения. Прав ли он?
Как мы знаем, что любое число возможно записано с применением десяти цифр: 0, 1, …, 9. Так как телефонные номера в большинстве случаев не начинаются с 0, то задача пребывает в вычислении числа комбинаций из девяти разных цифр по 7. Разумеется, что это ? размещение по семи разным местам семи из девяти разных цифр, т.е.
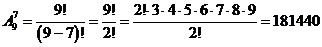номеров.
Кроме того в случае, если на диагностику одного номера тратить 1 60 секунд, то на все уйдет 3024 часа либо 126 дней. Так, следователь ? не прав.
4.какое количество методами семь различных книжек возможно поставить на полке в один последовательность?
Так как порядок книжек по условию ? значения не имеет, то имеем задачу о числе перестановок семи различных книг. Следовательно, способов.
5.В штате мебельного магазина имеется пять грузчиков. какое количество методами возможно организовать бригаду из двух грузчиков для доставки гарнитура к клиенту?
Потому, что не имеет значения, какой грузчик будет первым, а какой ? вторым, т.е. нужен выбор двух различных грузчиков из пяти вероятных, то это ? задача о сочетаниях из пяти человек по два. Следовательно,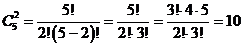 
способов.
6. В розыгрыше первенства по футболу среди институтов принимает участие 16 команд, наряду с этим каждые две команды играются между собой лишь один матч. какое количество всего календарных игр?
Эта задача ? о числе выборок из 16 по 2. Так,
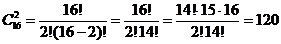игр.
7.Поменяем условия примера 3. Пускай поступила информация, что в телефонном номере преступника видятся лишь цифры 2, 4, 5 и 7. Как уменьшится перебор всех вероятных номеров?
Так, в семизначном телефонном номере видятся лишь четыре цифры, остальные три, разумеется, повторяют какие-то из имеющихся. Следовательно, имеем задачу о размещениях из четырех цифр по семи, другими словами с повторениями. Ответ: (повт.) = 47 =16384 номера. Перебрать все эти номера возможно приблизительно за 11 дней, что практически на порядок меньше, чем в примере 3.
8.какое количество методами возможно разложить в ряд две зеленые и четыре красные папки?
Так как заглавия папок не указываются, а критерием есть цвет, то задача пребывает в размещении шести цветных папок двух цветов. Имеем случай перестановок с повторениями. Следовательно,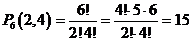 
методами.
9.какое количество методами возможно переставить буквы в слове «какао», дабы оказались все вероятные разные комплекты букв?
В заданном слове ? 5 букв, причем «к» и «а» повторяются по два раза, а «о» видится один раз. Так,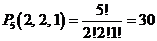 
способов.
Вопросы для самоконтроля:
1. Правило произведения.
2. Правило суммы.
3. его свойства и Факториал.
4. Размещения.
5. Размещения с повторениями.
6. Перестановки.
7. Перестановки с повторениями.
8. их свойства и Сочетания.
9. Сочетания с повторениями.
Тренировочные задачи
1. Вычислить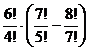 
Ответ: 1020
2.Посредством правила симметрии вычислить: .
Ответ: 26905
3.В учебной группе 12 студентов. какое количество методами их возможно разбить на бригады по 5 человек?
Ответ: 792
4. В своевременной группе имеется 14 солдат и 4 офицера. какое количество методами возможно назначить костюм, складывающийся из трех солдат и одного офицера?
Ответ: 2188
5. какое количество методами возможно составить шестизначное число, в состав которого входят две двойки и три шестерки?
Ответ: 60
6. какое количество методами возможно переставить буквы слове «каскад», дабы оказались все вероятные разные комплекты букв?
Ответ: 180