Расчётно-графическая работа № 1
Дано:
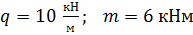
Отыскать:
Ответ
Рис. 1
Строим расчётную схему конструкции. Для этого освобождаем её от связей, заменяя их реакциями связей (рис. 2). Распределённую нагрузку заменяем сосредоточенной силой , приложенной в середине загруженного участка. Из схемы определяем:
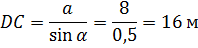
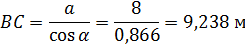
6
300
300
8 300
Рис. 2
Расчленяем совокупность по шарниру , заменяя его упрочнениями. Разглядываем сперва равновесие стержня (рис. 4). Составляем три уравнения равновесия стержня.
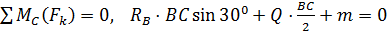(3)
Из уравнения (2) определяем упрочнение :
Из уравнения (3) определяем реакцию :
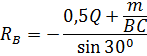
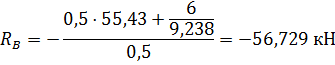
Из уравнения (1) определяем упрочнение :
6
300
300
8 300
Рис. 3 Рис. 4
Разглядываем равновесие ломаного стержня (рис. 3), приложив в шарнире упрочнения , направленные противоположно упрочнениям (численно ). Составляем три уравнения равновесия.
(6)
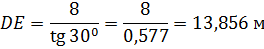
Из уравнения (4) определяем реакцию :
Из уравнения (5) определяем реакцию :
Из уравнения (6) определяем реактивный момент :
Ответ:
Расчётно-графическая работа № 2
Дано:
Выяснить: в момент, в то время, когда .
Ответ
2
3
Рис. 1
Разглядим перемещение неизменяемой механической совокупности, складывающейся из весомых тел 1, 2, 3 и 4, соединенных нитями. Изображаем действующие на совокупность внешние силы: , реакции и силу трения скольжения груза 1 о плоскость.
Используем теорему об трансформации кинетической энергии совокупности:
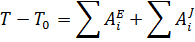
Так как совокупность складывается из полностью жёстких тел, соединённых нерастяжимыми нитями, то сумма работ внутренних сил совокупности равна нулю: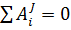 
. В начальном положении совокупность находится в покое, следовательно, . Тогда уравнение примет вид:
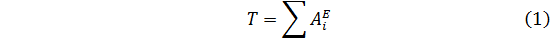
Кинетическая энергия совокупности в конечном положении равна сумме кинетических энергий всех весомых тел совокупности:
(2)
Кинетическая энергия груза 1, движущегося поступательно:
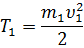
Кинетическая энергия тела 2, вращающегося около неподвижной оси:
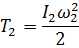
Кинетическая энергия тела 3, совершающего плоскопараллельное перемещение:
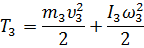
Кинетическая энергия груза 4, движущегося поступательно:
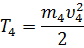
Моменты инерции тел равны (принимаем тела 2 и 3 за однородные диски):
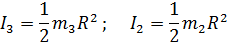
Подставив все данные в формулу (2), приобретаем:
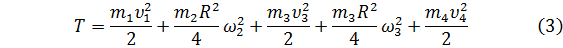
Высказываем входящие ко мне скорости через скорость груза 1. Из схемы определяем:
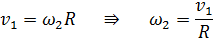
Точка есть МЦС катка 3, следовательно,
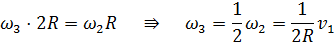
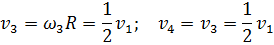
Подставляем полученные выражения скоростей в равенство (3):
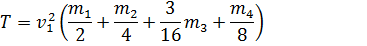
Учитывая данные задачи, приобретаем:
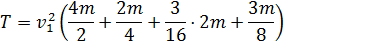
Либо
Находим сумму работ всех внешних сил, приложенных к совокупности, на заданном перемещении груза 1.
Работа силы трения груза 1:
Работы остальных сил равны нулю.
Высказываем перемещения через заданное перемещение груза 1. Наряду с этим учитываем, что зависимость между перемещениями такая же, как и между соответствующими скоростями. Из схемы находим:
Подставляем отысканные перемещения в выражения работ и определяем их сумму:
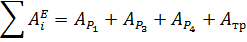
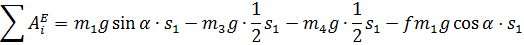
Либо
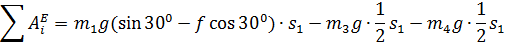
Подставив данные, приобретаем при :
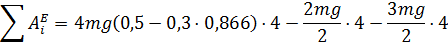
Либо
Работа всех сил на перемещении груза 1 отрицательная. Это указывает, что груз 1 движется в направлении, противоположном направлению, продемонстрированному на рисунке.
Применяя теорему об трансформации кинетической энергии, приравниваем выражения (4) и (5):
Из этого определяем скорость, которую получает тело 1:
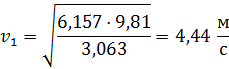
Ответ: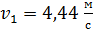 
Расчётно-графическая работа № 3
Дано:
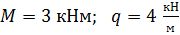
Отыскать:
Ответ
Рис. 1
Находим реакцию подвижной опоры , для чего в мыслях отбрасываем опору и заменяем её воздействие реакцией (рис. 2). Единственно вероятным перемещением стержня есть его поворот около шарнира на угол , к примеру, против часовой стрелки, наряду с этим часть балки повернётся около шарнира на угол . Составляем уравнение работ, высказывающих принцип вероятных перемещений. Наряду с этим учитываем, что работа силы при повороте тела равна произведению момента силы относительно центра вращения на угол поворота тела. Равномерно распределённую нагрузку заменяем сосредоточенной силой , приложенной в середине загруженного участка.
0,8м 1,6м 1,6м 2,4м
Рис. 2
Из схемы определяем . Из уравнения работ находим реакцию :
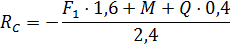
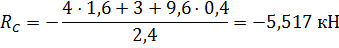
Находим реакцию подвижной опоры , для чего в мыслях отбрасываем опору и заменяем её воздействие реакцией (рис. 3). Единственно вероятным перемещением стержня есть его поворот около шарнира на угол , к примеру, против часовой стрелки. Наряду с этим часть балки повернётся около шарнира на угол . Составляем уравнение работ, высказывающих принцип вероятных перемещений. Наряду с этим учитываем, что работа силы при повороте тела равна произведению момента силы относительно центра вращения на угол поворота тела.
0,8м 1,6м 1,6м 2,4м
Рис. 3
На схеме из подобия треугольников определяем . Из уравнения работ находим реакцию :
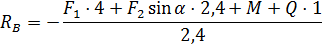
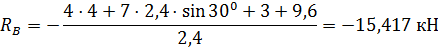
Для определения горизонтальной составляющей реакции твёрдой заделки отбрасываем сообщение, мешающую горизонтальному перемещению точки , заменив заделку ползуном в горизонтальных направляющих, жёстко скреплённым с балкой, и приложив реакцию (рис.4). Информируем ползуну вероятное перемещение . Вся балка будет выполнять поступательное перемещение вправо.
0,8м 1,6м 1,6м 2,4м
Рис. 4
Составляем уравнение работ:
Из этого находим реакцию :
Для определения вертикальной составляющей реакции неподвижной шарнирной опоры отбрасываем сообщение, мешающую вертикальному перемещению точки , заменив шарнир ползуном в вертикальных направляющих, жёстко скреплённым с рамой, и приложив реакцию (рис.5).
0,8м 1,6м 1,6м 2,4м
Рис. 5
Скажем ползуну вероятное перемещение . Наряду с этим балка возьмёт поступательное вертикальное перемещение, а балка повернётся около шарнира на угол . Все остальные точки не имеют вероятных перемещений. Составляем уравнение работ:
Из схемы определяем:
Находим реакцию :
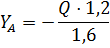
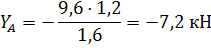
Для определения реактивного момента заменяем твёрдую заделку шарнирно-неподвижной опорой в точке , приложив к опоре реактивный момент (рис. 6).
0,8м 1,6м 1,6м 2,4м
Рис. 6
При сообщении совокупности вероятных перемещений балка повернётся около неподвижного шарнира на угол , а балка повернётся около шарнира на угол . На основании данных рис. 6 составляем уравнение работ всех сил на вероятных перемещениях балки:
Из расчётной схемы рис. 6 направляться, что .
Тогда из уравнения работ определяем реактивный момент:
Ответ: