Фонд оценочных средств с целью проведения промежуточной аттестации обучающихся по дисциплине (модулю)
Методика обучения математике
(наименование)
050100 Педагогическое образование
(направление подготовки)
бакалавриат
(уровень)
Формируемые компетенции:
ОК-1: обладает знаниями, навыками и умениями, соответствующими содержанию дисциплины «Методика обучения математике», формирующими культуру мышления, свойство к обобщению, анализу, восприятию информации, выбору путей и постановке цели ее успехи.
Знать:
- главные общекультурные сокровища.
Мочь:
- обобщать, разбирать, принимать данные;
- применять в учебно-воспитательном ходе современные образовательные ресурсы;
- учитывать разные контексты (социальные, национальные, культурные), в которых протекают процессы обучения, воспитания, социализации.
Обладать:
- культурой мышления;
- методами ориентации в опытных источниках информации (издания, сайты, образовательные порталы).
ПК-3: обладает знаниями, навыками и умениями, соответствующими содержанию дисциплины «Методика обучения математике», и готов использовать их в технологиях и современных методиках, готов применять способы диагностирования достижений обучающихся для обеспечения качества учебно-воспитательного процесса.
Знать:
- сущность главных понятий, применяемых в дисциплине «Методика обучения математике»;
- главные способы методики обучения математике;
- классическую и современную методику преподавания главных разделов и отдельных тем школьного курса математики.
Мочь:
- самостоятельно применять теоретические и практические знания для исполнения заданий характера и различного уровня сложности, как в рамках изучаемой дисциплины, так и в других дисциплинах, применяющих материалы данного кура;
- использовать полученные знания при ответе практических задач профессиональной деятельности.
Обладать:
- представлениями о связи методики обучения математике со школьным курсом математики, и другими дисциплинами;
- символикой изучаемой дисциплины;
- навыками методов дисциплины и применения понятий для ответа разных задач, применяемых в предстоящей учебной и профессиональной деятельности;
- навыками научного творчества.
ОПК-3: обладает терминологическим аппаратом дисциплины «Методика обучения математике», определяющим базы речевой опытной культуры педагога.
Знать:
- главные понятия методики обучения математике;
- особенности построения и основные правила устной и письменной речи в ходе обучения математике.
Мочь:
- оперировать понятиями методики обучения математике в устной и письменной речи;
- логически правильно строить устную и письменную обращение по математике.
Обладать:
- терминологией изучаемой дисциплины;
- навыками научного творчества.
Примерный список вопросов к экзамену (8 семестр)
- Анализ книжек по геометрии для 7-11 классов.
- Логическое строение школьного курса геометрии.
- Методика работы с геометрическими теоремами.
- Построения в курсе геометрии школы .
- Методика изучения геометрических размеров.
- Методика изучения треугольников.
- Методика изучения четырехугольников.
- Методика изучения окружности, его частей и круга.
- Методика изучения координат.
- Методика изучения векторов.
- Геометрические преобразования в школьном курсе геометрии
- Первые уроки геометрии (планиметрии, стереометрии): видящиеся пути и трудности их преодоления.
- Методика изучения параллельности на плоскости и в пространстве.
- Методика изучения перпендикулярности на плоскости и в пространстве.
- Методика изучения многогранников.
- Методика изучения тел вращения.
- Пропедевтика геометрического материала в курсе математики 5-6 класса.
Практические задания
1. Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке, лежащей на стороне BC. Отыщите BC, в случае, если AB = 30.
2. Расстояние от точки пересечения диагоналей ромба до одной из его сторон равняется 60, а один из его углов – 120°. Отыщите диагонали ромба
3. Четырехугольник ABCD обрисован около окружности радиуса R. Его диагональ BD проходит через центр окружности O. Отыщите MN, в случае, если M и N соответственно являются точками касания сторон BC и DC с указанной окружностью, 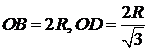 .
.
4. Углы B и C треугольника ABC равны соответственно 65° и 85°. Отыщите BC, в случае, если радиус окружности, обрисованной около треугольника ABC, равен 14.
5. Основания BC и AD трапеции ABCD равны соответственно 3 и 12. BD равняется 6. Докажите, что треугольники CBD и BDA подобны.
6.Докажите, что биссектрисы углов при основании равнобедренного треугольника равны.
7.На стороне AC треугольника ABC отмечены точки и без того, что . Докажите, что в случае, если , то .
8. Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно. Отыщите BN, в случае, если MN = 16, AC = 20, NC = 15.
9. Две параллельные плоскости, находящиеся на расстоянии 8 друг от друга, пересекают шар. Оказавшиеся сечения однообразны, и площадь каждого из них равна 9?. Отыщите площадь поверхности шара.
10. Высота цилиндра равна 3, а радиус основания равен 13.
а) Выстройте сечение цилиндра плоскостью, проходящей параллельно оси цилиндра, так, дабы площадь этого сечения равнялась 72.
б) Отыщите расстояние от плоскости сечения до центра основания цилиндра.
Радиус основания конуса равен 12, а высота конуса равна 5.