Задание
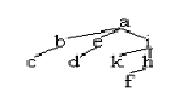
Для игры, заданной деревом (рис. 1), выяснить, кто из игроков имеет выигрышную стратегию, и указать ее.
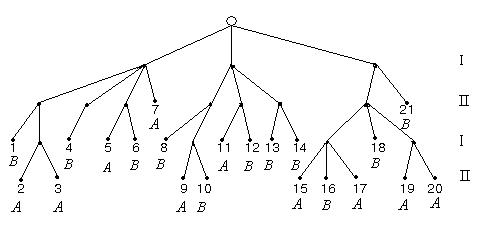
Рис. 1
Ответ
| № п/п | Методы | Конкретное соответствие задания заданному методу |
| Выяснить длину игры | Из рис. 1 видно, что большая протяженность цепи, идущей из корня в концевую вершину, равна 4; исходя из этого все вершины 4-го яруса – концевые, соответствуют последним пози-циям игры и помечены одним из знаков А либо В, определяющим выигрыш определенного игрока | |
| Начиная с вершин нижнего яруса, помечать вершины прошлого яруса знаками А либо В в зависимости от того, для какой из сторон подыгра, начинающаяся в данной вершине, есть выигрышной. Попутно отмечать ребра, каковые выяснят выбираемую стратегию | а) ребра, связывающие вершины 3-го и 4-го ярусов, изображают ходы игрока В (из нечетного яруса в четный). Каждую непомеченную вершину 3-го яруса a помечаем знаком В, в случае, если среди подчиненных ей вершин 4-го яруса имеется хотя бы одна вершина с меткой В, отмечаем кроме этого ребро ( ); в другом случае (в случае, если все подчиненные вершины – с меткой А) помечаем вершину знаком А и отмечаем любое ребро ( ). На рис. 1 ребра первого типа идут к вершинам 10 и 16, ребра второго типа – к вершинам 2 и 20; б) ребра, связывающие вершины 2-го и 3-го ярусов, изображают ходы игрока А (из четного яруса в нечетный). Каждую непомеченную вершину 2-го яруса помечаем знаком А, в случае, если среди подчиненных ей вершин 3-го яруса имеется вершина с меткой А; в другом случае (все подчиненные вершины – с меткой В) помечаем вершину знаком В в) вершины 1-го яруса и исходящие из них ребра помечаются так же, как обрисовано в п. а; вершина (единственная) 0-го яру-са, т.е. исходящие и корень дерева из него ребра – как в п. б. На рис. 2 расставлены приписанные метки и выделены отмеченные ребра 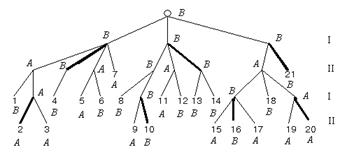 Рис. 2 |
|
| Выяснить побеждающую сторону | Знак, приписанный в следствии обрисованного процесса корню дерева, показывает, кто из игроков владеет выигрышной стратегией. Для данного примера выигрышная стратегия – у игрока В | |
| Указать выигрышную стратегию | Отмеченные ребра, исходящие из вершин, соответствующие ходам побеждающей стороны, составляют выигрышную стратегию. На рис. 2 – это отмеченные ребра, идущие из вершин 1-го и 3-го ярусов |
Решите самостоятельно следующие задачи:
1. Выяснить, кто из игроков владеет выигрышной стратегией, и указать ее для игры, заданной деревом на рис. 1, в случае, если концевые вершины 1-21 помечены следующим образом:
| 1) | В | А | А | А | В | В | А | А | А | В | В | А | А | В | А | В | В | В | А | В | А |
| 2) | В | В | А | А | В | В | А | В | А | В | В | В | А | В | А | А | А | В | В | А | А |
| 3) | В | А | А | А | В | А | В | А | В | А | В | А | В | В | В | А | А | В | А | В | А |
2. То же задание для игры, заданной деревом на рис. 3 с концевыми вершинами 1-24.
| 4) | В | А | В | В | В | А | В | А | В | А | А | В | А | В | А | А | А | В | В | В | А | А | В | А |
| 5) | В | А | А | В | А | В | А | В | А | В | В | А | А | В | А | В | А | А | В | А | В | В | А | В |
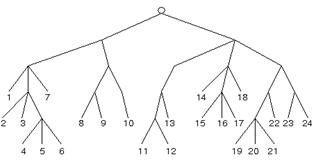
Рис. 3
ПРИЛОЖЕНИЯ
Приложение 1
Примеры ответа задач
Задача 1. какое количество 5-значных чисел, в десятичной записи которых участвуют цифры из множества {0, 1, 4, 6, 7}?
Ответ. В записи числа первая цифра должна быть хорошей от 0; остальные четыре цифры смогут быть произвольными. По комбинаторному правилу произведения искомое число 5-значных чисел равняется 4 • 5 • 5 • 5 • 5 = 2500.
Задача 2. какое количество 6-значных чисел, в десятичной записи которых участвуют цифры из множества {0, 1, 4, 6, 7} и таких, что четные цифры чередуются с нечетными ?
Ответ. В случае, если в записи числа первая цифра четная, то она предположительно составит 4 либо 6, вторая, шестая и четвёртая – 1 либо 7, третья и пятая – 0, 4 либо 6; таких чисел по правилу произведения:
2 • 2 • 3 • 2 • 3 • 2 = 144. В случае, если же первая цифра нечетная, то она, и третья и пятая могут быть равны 1 либо 7, вторая, шестая и четвёртая – 0, 4 либо 6; таких чисел 2 • 3 • 2 • 3 • 2 • 3 = 216. Всего искомых чисел 144 + 216 = 360.
Задача 3. какое количество разных слов возможно составить перестановками букв слова МАТЕМАТИКА?
Ответ. Число перестановок из 10 букв равняется 10!. Но в слове МАТЕМАТИКА
имеется однообразные буквы: М – 2 раза, А – 3 раза, Т – 2 раза: перестановка однообразных
букв не изменяет слова. Исходя из этого число разных 10-буквенных слов равняется 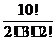 = =
= =
= 1 • 2 • 3 • 5 • 7 • 8 • 9 • 10 = [в произведении отсутствуют множители 4 и 6] = 151200.
Задача 4. В формуле W = [(X A Y) B (Y C Z)] D (X E T) F (Z G T) любой из знаков A, B, C, D, E, F, G обозначает одну из арифметических операций: сложение, вычитание, деление и умножение. какое количество разных формул представляются так?
Ответ. Любой из знаков A, B, C, D, E, F, G может иметь 4 значения независимо от вторых. Тем самым, формула конкретно определяется (4, 7)-размещением с повторениями. Исходя из этого число разных формул равняется 47 = 16384.
Задача 5. какое количество существует 7-значных десятичных чисел таких, что в их записи:
а) нет однообразных цифр в соседних разрядах;
б) в произвольных трех последовательных разрядах все цифры разны?
Ответ. а) Для первой цифры – 9 возможностей (каждая цифра, не считая 0); для второй и последующих – каждая цифра, не считая предыдущей, кроме этого 9 вариантов. Итог – по правилу произведения: 97.
б) Для первой и второй цифры – 9 возможностей, как в первом случае; для третьей и последующих – каждая цифра, не считая двух прошлых (они разны), т.е. 8 вариантов. По правилу произведения приобретаем: 92 • 85.
Задача 6.Каждое воскресенье любой из четырех теннисистов команды А проводит с кем-либо из четырех теннисистов команды В по одной игре. Доказать, что в течение шести месяцев найдутся два воскресенья с одним и тем же распределением соперников по четырем парам.
Ответ. Занумеруем игроков одной из команд. Распределение их соперников имеется перестановка из 4 элементов. Число n-перестановок Pnравно n! Следовательно, составлять разные комплекты из 4 пар возможно не более, чем 4! = 1 • 2 • 3 • 4 = 24 методами. Полгода составляют 26 недель, исходя из этого повторение неизбежно.
Задача 7. Дабы открыть входную дверь в пещеру, Али-Баба обязан предугадать шифр. Ему как мы знаем, что это некое число не дольше 5 цифр, записываемое с применением лишь цифр 2, 4, 8. Допустимо не более одной попытки в сутки. Удастся ли Али-Бабе попасть в пещеру в течение года?
Ответ. Указанные шифры – это слова в алфавите {2, 4, 8}. Число слов длины k в алфавите из трех букв равняется = 3k. Допустимые слова имеют длину от 1 до 5. Число всех таких слов равняется сумме 3 + 9 + 27 + 81 + 243 = 363. Исходя из этого за год возможно перебрать все вероятные шифры. Не позднее 363-го дня дверь откроется.
Задача 8. Книжный коллектор предлагает для комплектования библиотек книги
8 наименований по 1000 экземпляров любая. какое количество методами библиотека может составить заявку на 25 книг?
Ответ. Заявка показывает, сколько требуется книг каждого наименования. Запасы коллектора разрешают библиотеке выбирать в пределах общего количества 25 книг любое количество книг каждого наименования Соответствующая комбинаторная конфигурация имеется (8, 25) -сочетание с повторениями.
Число (n, k)-сочетаний с повторениями: = = . Для заданных параметров приобретаем: = = = (32 • 31 • . . . • 26) / (1 • 2 • . . .• 7) = 3365856.
Задача 9. Выстроить матрицу соседства вершин графа.
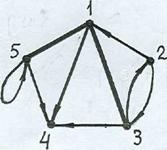
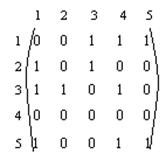
Ответ. В графе 5 вершин, исходя из этого матрица соседства вершин – 5-го порядка. Элемент aij матрицы равен 1, в случае, если из вершины i идет дуга (ориентированное ребро) в вершину j. Неориентированным ребрам (1, 3) и (1, 5) соответствуют в матрице по две единицы: a13 = a31 = 1; a15 = a51 = 1. Петле соответствует диагональный элемент a55.
Задача 10. По заданной матрице соседства вершин выстроить ориентированный граф. Выделить в этом графе какой-нибудь элементарный путь [1, 4] и какую-нибудь элементарную цепь [1, 4].
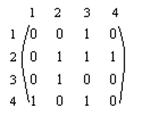
Ответ. Порядок матрицы равен 4. Исходя из этого в графе 4 вершины. Любая единица в матрице обозначает определенную дугу графа; число дуг равняется 7. Обозначим их a, b, c, направляться, e, f, g.
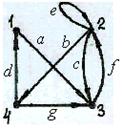
Путь [1, 4] = [1, a, 3, f, 2, b, 4]. Потому, что в графе нет кратных дуг (e и f – кратные ребра, но имеют различные направления), возможно опустить обозначения ребер: [1, 3, 2, 4]. В качестве цепи [1, 4] возможно разглядывать тот же путь, и цепи [1, d, 4], [1, a, 3, g, 4].
Задача 11. Отыскать число треугольников (полных трехвершинников) в полном графе K8.
Треугольник абсолютно определяется выбором трех вершин из данных восьми. Число таких неупорядоченных троек равно (8, 3)-сочетаний без повторений
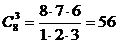 .
.
Задача 12.какое количество разных циклов длины 4 в полном двудольном графе K5,8 ?
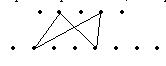
Ответ. Множество вершин двудольного графа разбивается на две части А = {ai } и В = {bj}. Любой цикл длины 4 в двудольном графе имеет форму а1b1a2b2a1; в полном графе таковой
цикл определяется выбором любых двух вершин а1и на данный момент2 из множества А и любых двух вершин
b1, b2 из множества В (см. чертеж). Неупорядоченную несколько вершин {а1, a2} возможно выбрать
С52 = (5 • 4) / (1 • 2) = 10 методами; неупорядоченную несколько вершин {b1, b2} возможно выбрать
С82 = (8 • 7) / (1 • 2) = 28 методами. По комбинаторному правилу произведения число разглядываемых циклов равняется С52 • С82 = 10 • 28 = 280.
Задача 13. Вершинами графа G являются все комплекты длины 5 из единиц и нулей. Ребра связывают все пары вершин, различающихся ровно в 2 разрядах. Выяснить число ребер графа G и его цикломатическое число.
Ответ.Число комплектов длины k из единиц и нулей равно (2, k)-размещений с повторениями: = 2k. Следовательно число вершин b графа G равняется 32. Степень s каждой вершины равна числу комплектов, разнящихся с данным в двух разрядах. Число пар таких разрядов равно (5, 2)-сочетаний без повторений: = 5 • 4 / 2 = 10. Для однородного графа степени s число ребер равняется b · s / 2 = 32 • 5 = 160.
Цикломатическое число связного графа ?(G) = p — b + 1 = 160 – 32 + 1 = 145.
Задача 14. Выстроить остов графа
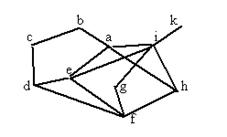
Ответ.Выбираем произвольную вершину, к примеру, а, включаем инцидентные ей ребра 1, 2, 3 и, следовательно, вершины b, e, i; потом соседние с ними вершины c, k, h, g и инцидентные им ребра 4, 5, 6, 7, и, наконец, вершины f, d и ребра 8, 9. Выбираемые ребра на каждом этапе подключают к уже выстроенному сейчас подграфу новую вершину, и исходя из этого циклов не появляется, а связность сохраняется. На чертеже выделенные ребра образуют остов графа. Схема показывает последовательность присоединения вершин в ходе построения остова.
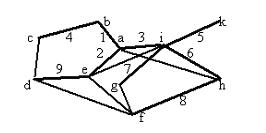
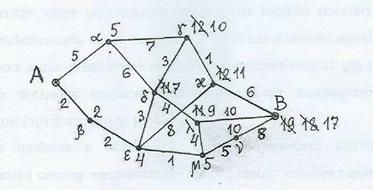
Задача 15. Отыскать расстояние между вершинами А и В графа с заданными длинами ребер.
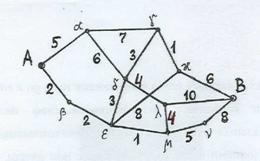
Ответ. Протяженность цепи – сумма длин ее ребер. Расстояние между вершинами – протяженность малейшей цепи, связывающей эти вершины. Метод нахождения искомого расстояния – на чертеже. Продемонстрирована расстановка меток, высказывающих длины цепей, связывающих данную вершину с входным полюсом А. По мере обнаружения более маленьких цепей метки пересчитываются (уменьшаются); минимальные вычисленные значения определяют расстояние от А до данной вершины. Последняя метка выходного полюса В имеется расстояние d(A, B). Для заданного графа d(A, B) = 17.
Приложение 2
Пример дерева игры
В п. 2.7 отмечалось, что в дереве игры «крестики-нолики» на доске 3´3 для 1-го хода начинающего игрока (назовем его +), в случае, если учитывать симметрию, число возможностей сводится до 3: «центр» — b2, «угол» — a1, «середина стороны» — b1. Для ответного хода игрока В (его конечно назвать 0) — выбор из 8 оставшихся полей, в случае, если учитывать симметрию, зависит от хода, выбранного начинающим и т.д.
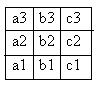
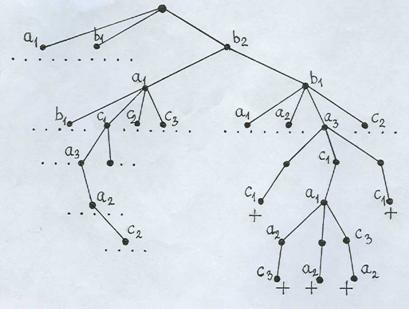
На рис. фрагменты дерева игры: на первом ярусе 3 вершины: a1, b1, b2;
продолжено изображение лишь ответов на ход b2 (с учетом симметрии их 2): «угол» — a1, «середина стороны» — b1. На ход а1 игрока 0у игрока +имеется 4 значительно разных ответа;
на ход с1 – указана (не до конца) лишь форсированная ветвь, которая ведет к ничейному финалу. В случае, если же на 2-м ярусе игроком 0был выбранход b1, у игрока +кроме этого имеется 4 сущест-венно разных ответа: на рисунке указано лишь продолжение при выборе хода а3: при всех ответах игрока 0 — форсированный выигрыш +.
ГЛОССАРИЙ
| № п/п | Новое понятие | Содержание |
| Выборка количества k из n элементов, либо (n, k)-выборка | комплект элементов (xi1, xi2,…, xik), составленный из элементов множества Х = {x1, x2,…, xn} | |
| (n,k)-размещение без повторений | упорядоченная (n,k)-выборка, в которой элементы не смогут повторяться | |
| (n,k)-размещение с повторениями | упорядоченная (n,k)-выборка, в которой элементы смогут повторяться; слово длины k в алфавите из n букв | |
| n-перестановка, либо перестановка из n элементов | (n,n)-размещение без повторений | |
| (n,k)- сочетание без повторений | неупорядоченная (n,k)-выборка без повторений; k-элементное подмножество n-элементного множества | |
| (n,k)- сочетание с повторениями | неупорядоченная (n,k)-выборка с повторениями | |
| Биномиальные коэффициенты | числа (n,k)-сочетаний без повторений, совпадающие с коэф-фициентами формулы двучлена Ньютона для n-й степени двучлена (x+y): (x+y)n = 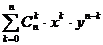
|
|
| Треугольник Паскаля | треугольная числовая таблица, n-я строчок которой складывается из (n + 1) коэффициентов двучлена (x+y)n: ,, … , . Каждое число строчка, не считая крайних, равных единице, равняется сумме двух ближайших чисел, находящихся над ним в прошлом последовательности | |
| Полиномиальный коэффициент | коэффициент при произведении • •…• в разложении полинома (x1+ x2+…+ xn)n по степеням переменных x1, x2,…, xn | |
| Принцип Дирихле (принцип коробок) | комбинаторное соотношение: в случае, если в m коробках находятся (m+1) либо больше камней, то хотя бы в одном из коробок больше одного камня | |
| Граф | совокупность G = (V, E), складывающаяся из множества элементов V = {v}, именуемых вершинами множества и графа элементов E = {е}, именуемых ребрами; каждому ребру е I Е поставлена в соответствие упорядоченная либо неупорядоченная пара элементов v1, v2I V, именуемых финишами ребра е = (v1, v2) | |
| Инцидентность | отношение между вершиной v и ребром е графа, в случае, если вершина v есть финишем ребра е | |
| Соседние (смежные) вершины | две вершины, инцидентные одному и тому же ребру | |
| Смежные ребра | два ребра, инцидентные одной и той же вершине | |
| Матрица инциденций графа с b вершинами и p ребрами | прямоугольная матрица А = ¦aij¦ с b строчками и p столбцами; строчки соответствуют вершинам графа, столбцы – ребрам, причем для неориентированного графа элемент матрицы aij равен 1, в случае, если вершина vi и ребро ej инцидентны, и равен 0 в другом случае. Для ориентированного графа aij = -1, в случае, если vi есть началом дуги ej; aij = +1, в случае, если vi — финиш дуги ej; aij = 0, в случае, если вершина vi и ребро ej не инцидентны. Петле соответствует элемент, равный 2 | |
| Матрица соседства (смежности) вершин графа с b вершинами | квадратная матрица В = ¦aij¦ размерности b, строки и столбцы которой соответствуют вершинам графа; элемент bij равен числу ребер, идущих из вершины vi в вершину vj. | |
| Изоморфизм графов | графы G1 = (V1, E1) и G2 = (V2, E2) изоморфны, в случае, если существуют взаимно однозначные отображения f: V1® V2 и g: E1® E2, сохраняющие инцидентность | |
| Полный граф | граф без кратных ребер (и время от времени без петель), в котором две каждые вершины соединены ориентированным либо неориентированным ребром. Полный неориентированный граф без петель Kb с b вершинами содержит ребер | |
| Двудольный граф | граф, множество вершин которого разбито на два непересекающихся класса: V = E , а ребра связывают вершины лишь из различных классов | |
| Степень s(?) вершины ? | для графа без петель – число ребер в звезде Z?. Сумма степеней всех вершин графа равна удвоенному числу ребер | |
| Подграф | часть графа, если она есть графом, т.е. вместе с каждым ребром в подграф должны включаться оба финиша ребра | |
| Путь [?, ?] | последовательность ребер графа, образующая постоянную траекторию по вершинам и рёбрам графа, согласованную с ориентацией ребер; (? – начало, ? – финиш пути) | |
| Цепь [?, ?] | последовательность ребер графа, образующая постоянную траекторию, связывающую вершины ? и ?, в случае, если вычислять все ребра графа неориентированными; (? и ? – финиши цепи) | |
| Контур (соотв. цикл) | путь (соотв. цепь) с совпадающими финишами | |
| Связный граф | граф, каждые две вершины которого связаны цепью | |
| Расстояние d(v1,v2) между двумя вершинами неориентированного связного графа | число ребер (либо сумма длин ребер, в случае, если ребрам приписаны длины), минимальное среди всех цепей, связывающих v1и v2 | |
| Дерево | связный граф без циклов, т.е. граф, все ребра которого ациклические. В любом конечном дереве число ребер на 1 меньше числа вершин | |
| Корневое дерево | дерево, в котором выбрана вершина (корень); множество вершин дерева разбивается на ярусы по величине расстояния до корня | |
| Остов графаG | подграф D, содержащий все вершины графа G и являющийся деревом. Довольно остова D все ребра подграфа G \ D именуются хордами | |
| Четный (эйлеров) граф | граф, степени всех вершин которого — четные числа. | |
| Гамильтонов путь | элементарный путь, проходящий через все вершины графа по одному разу | |
| Цикломатическое число ?(G) размерность и | графа подпространства четных подграфов в линейном пространстве всех подграфов графа G.В графе с p ребрами, b вершинами и k компонентами: ?(G) = p — b + k; для связного графа ?(G) = p — b + 1 | |
| (k, l)-полюсник | сеть с (k + l) выделенными вершинами — полюсами, разбитыми на два класса: k входных и l выходных полюсов. (1, 1)-полюсник именуется двухполюсной сетью | |
| Параллельно-последовательная сеть | сеть, полученная из однореберных сетей в следствии конечного числа параллельных и последовательных соединений. Класс параллельно-последовательных сетей (сокращенно, ?-сетей) определяется индуктивно: (1) однореберная сеть имеется ?-сеть; (2) в случае, если S1и S2- ?-сети, то S1• S2и S1U S2кроме этого?-сети | |
| Поток в сети с заданными пропускными свойствами ребер | пара (f, w), где w – некая ориентация всех неориентированных ребер сети, а f(e) – заданная на множестве всех ребер сети функция с неотрицательными значениями, не превосходящими пропускных свойств ребер с(е), и такая, что в каждой внутренней вершине сумма значений потока по ребрам, входящим в вершину, равна сумме значений потока по ребрам, исходящим из вершины | |
| Сечение в сети | множество ребер, блокирующее все цепи из ?S в ?S. При его удалении сеть делается несвязной, причем полюсы ?S и ?S попадают в различные компоненты связности | |
| Теорема Форда-Фалкерсона о большом потоке | большая величина потока Rmaxчерез сеть S равна минимальной из пропускных свойств сminее несложных сечений | |
| Дискретная игра | совокупность, воображающая собой: дискретное множество обстановок; правила игры, определяющие вероятные переходы из одной ситуации в другую; подмножество последних обстановок, в каждой из которых выяснен итог игры (выигрыш первого, выигрыш второго, ничья) | |
| Игра двух лиц с открытой информацией | игра с поочерёдными ходами игроков, в которой на каждом шаге обоим игрокам известна текущая обстановка | |
| Стратегия f игрока A | соответствие , назначающее для каждой ситуации , в которой может оказаться игрок A, один определенный движение из множества допустимых | |
| Выигрышная стратегия | стратегия, выбор которой игроком ведет к обстановке его выигрыша при любом выборе стратегии соперника | |
| Беспроигрышная стратегия | стратегия, выбор которой игроком ведет к обстановке его выигрыша либо ничьей при любом выборе стратегии против-ника | |
| Хроматическое число графа | Предельное количество красок, которыми возможно верно раскрасить все вершины графа |