Пункт 1. Вычисление площадей фигур.
Так как площадь криволинейной трапеции связана с интегралом, то это приложение разумеется. Но имеется особенности, связанные со строением фигуры , в некоторых случаях нужно разбить фигуру на пара частей.
Пример. Отыскать площадь фигуры, ограниченной линиями .
Ответ. Выстроим чертёж:
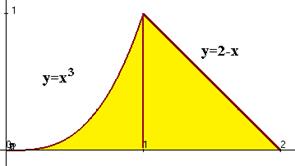
Так как верхняя граница по окончании точки 1 переходит с одной кривой на другую, то нужно будет разбить на сумму двух вычислений по каждой части раздельно: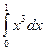 
+ 
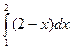. Итак, возьмём 
= 
= 
= 
.
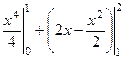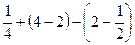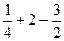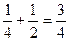Пункт 2. Вычисление количеств тел вращения.
В случае, если график функции вращать около оси 0x, то окажется так именуемое тело вращения. Каждое сечение плоскостью, паерпендикулярной оси 0x , это круг, его площадь равна , так как это именно и имеется радиус (равняется удалению вращающейся точки от оси вращения). В итоге,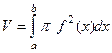 
.
Пример. Вывести этим способом формулу количества шара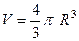 
.
Ответ. Чтобы получить шар, достаточно вращать верхнюю полуокружность, которая задаётся таковой функцией: .
= 
= 
=
= 
= 
.
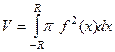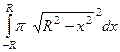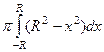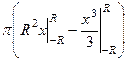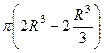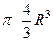Пункт 3. Вычисление длины дуги кривой.
Формула для очевидно заданной кривой: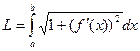 
.
Подтверждение.Разобьём область определения на n частей, разглядим подробнее одну часть графика.
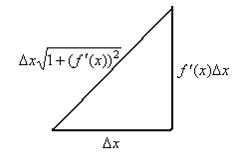
Протяженность фрагмента кривой приближённо равна гипотенузе. Наряду с этим, тангенс угла наклона равен производной. Исходя из этого, в случае, если горизонтальный катет то вертикальный равен . Но в этом случае гипотенуза, по теореме Пифагора, равна:
= = .
При переходе к пределу при , окажется .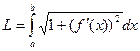
Чем круче наклон фрагмента графика, тем больше величина , и тем больше корень и соответственно, протяженность части данной кривой. Наоборот, в случае, если график горизонтальный (функция = константа) то = . Протяженность таковой кривой легко равна длине отрезка в области определения, другими словами .
Для параметрически заданной в плоскости формула принимает таковой вид: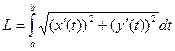 
.
В трёхмерном пространстве: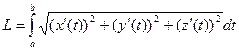 
.
Протяженность кривой в полярной совокупности координат.
Пускай кривая задана формулой .
Тогда: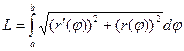 
.
Подтверждение данной формулы. Разглядим формулы связи между полярными и декартовыми координатами:
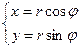
Сейчас применим параметр таким же образом, как в прошедшей формуле был параметр .
, .
Отыщем производные:
Их нужно подставить в формулу: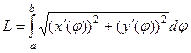 
.
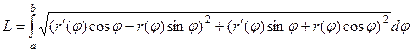
применим формулу сокращённого умножения в каждом квадрате под корнем. В том месте окажутся удвоенные произведения и квадраты, каковые, но, сократятся, поскольку они будут различного символа. Выражение под корнем преобразуется так:
=
+
=
=
.
Исходя из этого и получается в итоге: .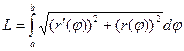
ЛЕКЦИЯ № 4. 07.03.2017
Несобственный интеграл.
В случае, если криволинейная трапеция вечно вытянута вправо либо вверх, то возможно конечная площадь. Примеры:
Пример.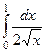 
= = 1.
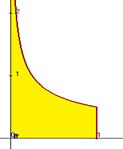
Но так как область значений E(f) не есть ограниченной. При вычислении мы кроме того и не увидели, что функция неограниченная в окрестности точки 0, т.е.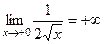 
. Так как первообразная ограниченная, и в неё возможно и . Вот график данной функции 
:
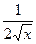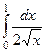возможно разглядывать как предел 
.
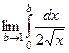Пример. Вычислить .
Ответ. Таковой интеграл возможно разглядывать как предел интегралов вида при . В случае, если вычислить то окажется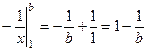 
. Предел 
.
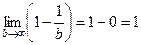Не обращая внимания на неграниченность трапеции под интегралом, площадь конечна. Тут область определения D(f) не есть ограниченной. Однако, трапеция через чур узкая, т.е. её ширина убывает достаточно скоро, дабы площадь не превысила некое число. Так возможно, например, в случае, если площади криволинейных трапеций между соседними целыми абсциссами убывают со скоростью сходящейся геометрической прогрессии.
Определение. В случае, если функция выяснена и постоянна на , то предел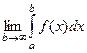 
именуется несобственным интегралом 1-го рода от функции , и обозначается 
.
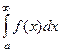Подобно посредством предела возможно выяснить и несобственный интеграл 2 рода. Так, в случае, если функция имеет нескончаемый предел на правой границе b то нужно отойти на некое расстояние и посчитать конечный интеграл, а после этого перейти к пределу.
Определение. В случае, если функция выяснена и постоянна на и наряду с этим предел , то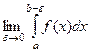 
именуется несобственным интегралом 2-го рода от функции , и обозначается 
.
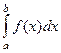Итак, в случае, если неограниченная D(f), то интеграл именуется несобственным интегралом 1-го рода, а вдруг E(f) то несобственным интегралом 2-го рода.
В случае, если предел существует и есть конечным числом, то несобственный интеграл именуется сходящимся, в случае, если предел не существует либо равен бесконечности, то интеграл именуется расходящимся.
Кстати, для сравнения, геометрическая прогрессия также бывает сходящейся или расходящейся. В случае, если площадь таковой вечно вытянутой криволинейной трапеции разбить на части по целым числам, к примеру от 1 до 2, от 2 до 3 и без того потом, то если они образуют сходящуюся прогрессию, и в сумме равны некоей константе, то интеграл сходится.
Примеры расходящихся несобственных интегралов.
Пример.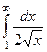 
= = . Тут расходимость из-за неограниченности первообразной.
Пример.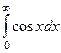 
= 
= 
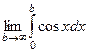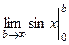= = . Но данный предел не существует, синус колеблется от -1 до 1 и при повышении переменной его график не пытается ни к какой конкретной высоте. И не смотря на то, что кроме того функция ограничена, несобственный интеграл расходится. Площадь криволинейной трапеции, при повышении , то растёт, то опять убывает.
Пример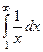 
= 
= 
= = = .
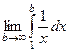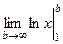Примеры сходящихся несобственных интегралов.
Пример.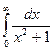 
= 
= .
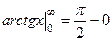Пример.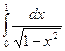 
= 
= .
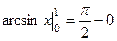Теорема 1. Несобственный интеграл 1-го рода
сходится тогда и лишь тогда, в то время, когда ,
несобственный интеграл 2-го рода
сходится тогда и лишь тогда, в то время, когда .
Подтверждение. Сперва разглядим первообразную.
= = 
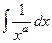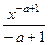, что возможно записать в виде 
.
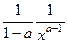В случае, если пределы интегрирования от 1 до , то не нескончаемый итог окажется только в том случае, в то время, когда переменная в знаменателе, другими словами степень , другими словами , другими словами .
А вдруг пределы интегрирования от 0 до 1, то напротив, наличие переменной в знаменателе ведет к тому, сто предел нескончаем, интеграл расходится. Другими словами для сходимости, нужно дабы степень была такая, дабы переменная пребывала конкретно в числителе. Тогда , другими словами, , . Что и требовалось доказать.
Обратите внимание, что при расходятся оба этих интеграла, поскольку первообразная -это логарифм, а он не ограничен ни при , ни при .
Для таких интегралов 2 рода, для сходимости нужно, дабы степень перешла в хорошие, к примеру, в случае, если у функции степень , а у первообразной на 1 больше, уже . В случае, если же она , то по окончании интегрирования станет , другими словами ещё не переходит через 0 в хорошие.
Примеры
| 1 рода |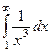 
|
|
|
|
|
|
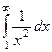
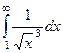
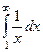
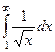
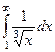
| 2 рода |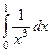 
|
|
|
|
|
|
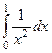
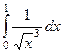
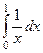
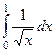
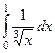
| 1,5 | 1/2 | 1/3 |
Жёлтым цветом тут выделены сходящиеся интегралы.
Теорема 2. Несобственный интеграл сходится первообразная на границах интегрирования имеет конечный предел.
Мысль доказательства. Вправду,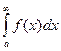 
= = 
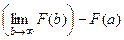. Второе слагаемое конечное число. Первое слагаемое (предел) имеется конечное число тогда и лишь тогда, в то время, когда разность — конечное число. Другими словами, сходятся конкретно те несобственные интегралы, где график первообразной стабилизируется по высоте, т.е. имеет конечный предел . В случае, если интеграл 1 рода, то равносильно сходимости.
Следствие (нужный показатель сходимости).
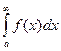сходится .
Вправду, в случае, если то = = .
Замечание. Это нужный, а не достаточный показатель, другими словами, из сходимости направляться, что f пытается к 0, но не наоборот. Другими словами, при смогут быть как сходящиеся, так и расходящиеся интегралы, а вот в случае, если , тогда лишь расходящиеся.
Разглядим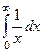 
и 
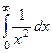. Тут и в том и другом случае выполнено. А однако, первых из них расходится, а второй сходится. Их графики кажутся похожими, но так как второй значительно уменьшается значительно стремительнее: так, при значение у первой их них , а у второй , другими словами в 1000 раз меньше! Другими словами не считая условия ответственна ещё и скорость сходимости. Но в случае, если это условие не выполнено, то сходимости совершенно верно нет, в этом и состоит понятие «нужный» показатель.
Как мы заметили, овольно нередкой есть обстановка, в то время, когда производная пытается к бесконечности, а сама функция (другими словами её первообразная) в той же точке есть конечной. Геометрическая интерпретация. Разглядим верхнюю полуокружность. При приближении к точке (1,0) касательная пытается к вертикальному положению, тангенс угла её наклона к . А наряду с этим сама полуокружность ограничена по высоте:
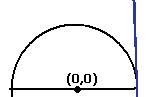
Теорема 3. Пускай . Несобственный интеграл 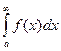сходится тогда и лишь тогда, в то время, когда сходится 
.
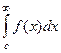Мысль доказательства. Вся площадь равна . Наряду с этим заведомо есть конечной, в этом случае число само собой разумеется тогда и лишь тогда, в то время, когда само собой разумеется. Чертёж:
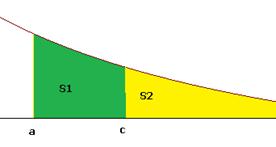
Теорема 4. Показатель сравнения в конечной (непредельной) форме.
В случае, если и сходится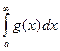 
, то сходится .
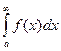Вправду, в случае, если интеграл для большей функции равен C, то для меньшей он меньше чем C, другими словами, не равен бесконечности.
Пример.Узнать сходимость интеграла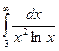 
.
Учитывая тот факт, что при правильно , получается
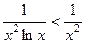. Тогда 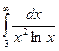, а он сходится, поскольку степень знаменателя больше 1. Тогда и исходный интеграл сходится.
Замечание. Подобно тому, как мы ограничиваем сверху какой-либо сходящейся функцией, возможно сократить снизу какой-либо расходящейся функцией. В случае, если интеграл от данной меньшей функции расходится, то и исходный также расходится.
Теорема 5. Показатель сравнения в предельной форме.
В случае, если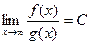 
, причём C превосходно от 0 и от (другими словами и бесконечно малые одного порядка). Тогда:
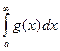сходится тогда и лишь тогда, в то время, когда 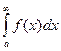сходится.
Пример на показатель в предельной форме.
Узнать сходимость интеграла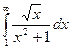 
.
Разглядим для функции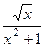 
более легко устроенную, но эквивалентную ей , котрую возможно записать в виде .
Предел их отношения равен 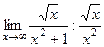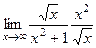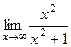1:
= 
= 
= 1.
Тогда сходимость первого интеграла равносильна сходимости второго, другими словами возможно разглядывать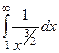 
. Степень 
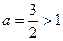, исходя из этого интеграл сходится.
Эти показатели разрешают сравнивать интегралы, которые содержат громоздкие функции, с какими-то более несложными «эталонными», к примеру, степенными.
Замечание. В прошлом примере мы разглядывали по старшей степени, а в подобной обстановке для интегралов 2 рода нужно определять степень суммы по младшей степени. Для интегралов 2 рода верны подобные показатели сравнения, но в предельной форме сравнение происходит по мельчайшей степени.
Кратные интегралы.
Определение. Пускай дана функция , её область определения — некая область D в плоскости. Введём разбиение D на части двумя семействами прямых линий. В каждой части заберём произвольную точку с координатами . Площадь обозначим . Величина именуется интегральной суммой. Предел данной величины при измельчении разбиения именуется двойным интегралом функции по множеству , и обозначается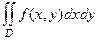 
.
В большинстве случаев, сперва будем разглядывать область D — прямоугольник: , .
Геометрический суть. Интегральная сумма свидетельствует сумму количеств параллелепипедов, выстроенных на каждом из оснований , а интеграл — количество под поверхностью, которая задана уравнением .
Физический суть. В случае, если функция задаёт плотность какой-либо плоской пластины, то двойной интеграл — масса.
Подобно определяется понятие тройного интеграла. В случае, если дана функция , определённая в трёхмерной области, то её возможно разбить на части посредством трёх семейств плоскостей, выбрать по точке в каждой части, и составить интегральную сумму. То, что получается в пределе, именуется тройным интегралом.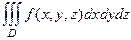 
. Физический суть тройного интеграла: в случае, если функция — плотность некоей породы, то в следствии вычисления тройного интеграла окажется масса.
Способ вычисления.
При вычислении кратных интегралов, как двойных, так и тройных, сводят к так называемым «повторным» интегралам.
= 
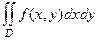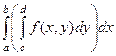. Кроме этого в этом случае возможно использовать запись вида: 
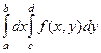где дифференциал пишется конкретно по окончании того интеграла, которому он соответствует. При фиксировании одной переменной, мы приобретаем функцию уже не двух, а одной переменной. Так, при получается . На чертеже этому соответствует сечение поверхности на протяжении оси , другими словами кривая. Интеграл по одной переменной при фиксированной второй, это площадь криволинейной трапеции, которая получается в сечении.
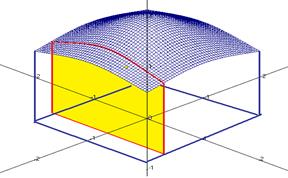
В случае, если проинтегрировать все эти величины по второму направлению, то окажется количество тела под поверхностью.
Подобно, в случае, если разрезать булку хлеба на тонкие слои, а после этого вычислить площадь каждого, и сложить все эти величины, умножая наряду с этим на их толщину, то возьмём количество.
Пример. Вычислить интеграл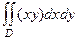 
, где имеется квадрат: , .
Ответ.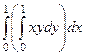 
= 
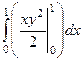вычислили сперва «личную первообразную» по переменной , другими словами ту функцию, личная производная от которой по была бы . Во внутренних скобках используем формулу Ньютона-Лейбница по переменной .
= 
= 
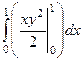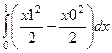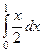. Оставшийся интеграл по переменной вычисляется простым образом: = = .
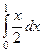Но, область D возможно и не прямоугольной. Подобно тому, как массив в программировании возможно не прямоугольным, тогда во внутреннем цикле двойного цикла границы переменные и зависят от переменной, определённой во внешнем цикле:
for i : = 1 to 10 do
for j : = 1 to i do
read (a[i,j]);
end;
end;
, если область не прямоугольная, границы положенного интеграла смогут быть не числами, а зависеть от внешней переменной. Разглядим пример.
Пример.Вычислить 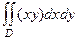, где , D — треугольник с вершинами (0,0), (1,0), (1,1).
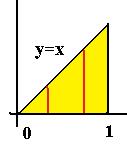
Ответ.Границы фигуры по переменной это , при вторых значениях нет точек этого треугольника по большому счету. При каждом , вертикальный отрезок имеет различную высоту, сперва по большому счету 0, а после этого чем правее, тем больше. Чем больше , тем выше отрезок по . Вертикальные отрезки в треугольника от высоты 0 доходят до линии . Исходя из этого при каждом , правильно .
Интеграл будет записан в виде: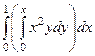 
.
Граница во внутреннем интеграле зависит от внешней переменной .
Границы внешнего интеграла непременно должны быть контантами.
Во положенной скобке, вычислится первообразная по , и будет применена формула Ньютона-Лейбница по .
= 
= 
= 
.
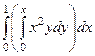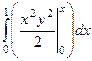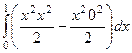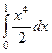И не смотря на то, что границы зависят от , они подставлены в переменную , т.е. всё равняется оказалась функция от , так же, как в случае, если был бы прямоуголник и границы были бы числовыми. Потом, уже простым путём вычислим интеграл по .Итак, = = .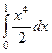
ЛЕКЦИЯ № 5. 14.03.2017
Математика без Ху%!ни. Определенные интегралы, часть 3. Площадь фигуры.
Интересные записи:
- Принятие решения о проведении проверки
- При оказании помощи надо обращаться к компетентным источникам, себя расценив как не вполне компетентный источник.
- При работе повар обязан выполнять правила техники безопасности согласно ти р м-045-2002
- Природа и человек, его внутренний мир, природа и любовь, природа и взаимоотношения людей: в аспектах