Фэй Дж. Кросби, Калифорнийский университет, Санта-Крус
Чтобы оценить эффект Акции помощи, необходимо, во-первых, знать, что есть Акцией помощи, а что — нет. В соответствии с трактовкой Американской психотерапевтической ассоциации Акция помощи имеет место, в то время, когда какая-либо организация прилагает громадные упрочнения чтобы удостовериться в отсутствии дискриминации в совокупности образования и трудоустройства и что, наоборот, любой имеет равные возможности (АРА, 1995). Акция помощи выходит за пределы той политики, при которой в принципе выполняют условия справедливости, но предпочитают, дабы неприятность разрешилась сама собой, без принятия каких-либо активных мер. Для Акции помощи нужны средства и постоянная бдительность. Она не требует и не вводит квот, принесения в жертву стандартов для разнообразия и не заменяют собой заслуженные льготы (Turner Pratkanis, 1994).
В области занятости закон об Акции помощи стал серьезно использоваться в Соединенных Штатах в 1965 году (Holloway, 1989). Сейчас он соблюдается во всех правительственных учреждениях и в большинстве организаций, каковые трудятся на федеральное правительство. Благодаря программе Акции помощи принимается на работу двадцать пять процентов жителей США (Crosby Cordova, 1996)!
Как трудится эта совокупность? Поразмыслите о ваших учителях как о служащих данного учебного заведения. Представьте, что 10% ваших учителей социальных наук — дамы (применение = 10%). Доступность данной работы для дам рассчитывается в первую очередь из доли дам, имеющих степень врача философии в области социальных наук. В случае, если 30% врачей философии в социальных науках — дамы, тогда как учителей — лишь 10%, то что-то неправильно! Найденные неприятности должны быть решены. Корректирующие меры смогут включить эластичные цели (но не твердо установленные квоты) и реалистические графики работы.
Каков эффект Акции помощи в области занятости? Экономисты установили, что представители и белые женщины национальных меньшинств, каковые взяли работу в рамках программы Акции помощи, находятся в более удачном положении с позиций найма, сохранения рабочего места, продвижения и оплаты по работе (Kravitz et al., 1997). Ощущают ли себя люди и белые женщины из национальных меньшинств взявшими в следствии Акции помощи какой-то ярлык, свидетельствующий об их неполноценности? В большинстве случаев, нет. Ощущают ли белые приятели недовольство либо ужас? Кое-какие ощущают, в особенности если они расисты либо женофобы либо если они отождествляют Акцию помощи с квотами (Golden, Hinkle Crosby, 1998); но практически большая часть ничего аналогичного не чувствуют. В действительности, три четверти американцев одобряют Акцию помощи (Tomasson, Crosby Herzbergen 1996).
Многие белые приятели, включая глав некоторых больших корпораций, поддерживают Акцию помощи, придерживаясь реалистичной точки зрения на экономику. В то время, когда создаются условия для приема на работу белых представителей и женщин этнических меньшинств, то наряду с этим появляются и новые возможности показать себя гениальным белым мужчинам, каковые до того не имели никаких преимуществ. Компании, участвующие в программе Акции помощи, по-видимому, более рентабельны, чем другие организации (Reskin, 1998). Подобно действенным пожарным командам, где человек невысокого роста может пролезть в узкий проход, тогда как большие люди руководят громоздким оборудованием, опытные команды с разнородным составом, по-видимому, имеют конкурентные преимущества (Leonard, 1986).
В области образования Акция помощи кроме этого подразумевает такие шаги, как корректировка и контроль. В случае, если при осуществлении контрольных мер обнаруживается, к примеру, что латиноамериканцы составляют меньшинство от всего числа студентов, чем ожидается исходя из общего числа выпускников средних школ, предпринимаются определенные шаги, корректирующие обстановку (к примеру, программы помощи нуждающимся в ней). Акция помощи в области образования не должна повлечь за собой понижения принятых стандартов; наряду с этим при помощи тщательного, а иногда больного изучения должен быть отыскан ответ на следующие вопросы: 1) какие конкретно качества мы ценим в человеке; 2) как мы можем точно оценить их; 3) на какие конкретно группы мы можем поделить людей.
не сильный местом программы есть то, что в следствии ее применения цветные студенты и белые чувствуют себя разобщенными. Никому не понравится услышать, что своим продвижением он обязан скорее неоправданным льготам, включая квоты, чем собственным заслугам (Heilman, 1994). К счастью, большая часть людей, на которых направлены подобные меры, не путают Акцию помощи с квотами (Truax, Wood, Wright, Cordova Crosby, 1998), особенно в случае, если чувствуют себя защищенными в собственной этнической индивидуальности (Schermund, Sellers, Mueller Crosby, 1998).
В недавних примечательных изучениях, совершённых бывшими ректорами Принстона и Гарварда, были обнаружены хорошие результаты учета этнической принадлежности абитуриентов при приеме в университеты и колледжи. Боуэн и Бок (Bowen Bok, 1998) обратили внимание на долгосрочный эффект для сотен чернокожих студентов, каковые были приняты в 24 элитных колледжа в 1951, 1967 и 1989 годах благодаря программе Акции помощи. Чернокожие студенты оканчивали обучение и приобретали ученые степени по таким же нормам, что и белые студенты. Чернокожие выпускники университетов кроме того чаще, чем белые, становились гражданскими фаворитами, отдавая дань обществу, которое их воспитало!
Так каков же в целом эффект использования на практике программы Акции помощи в области образования? Он огромен. Эта программа нужна для всех.
—
Приложение. измерения и Статистические методы
Большая часть работы психолога складывается из проведения измерений — или в лаборатории, или в поле. Это смогут быть измерения перемещений глаз младенца при первом действии нового стимула; регистрация кожно-гальванической реакции людей на протяжении стресса; подсчет числа попыток, нужных для обуславливания мартышки с префронтальной лоботомией; определение показателей вступительных оценок среди учеников, применяющих компьютеризованное обучение, либо подсчет количества больных, у которых наступило улучшение по окончании того либо иного вида психотерапии. Во всех этих примерах операция измерения дает числа; задача психолога — трактовать их и прийти к некоему неспециализированному выводу. Главный инструмент для данной задачи — статистика, дисциплина, имеющая дело со сбором числовых данных и проведением заключений на их базе. Цель разрешённого приложения — рассмотреть кое-какие статистические способы, играющие ключевую роль в психологии.
Это приложение написано в предположении, что неприятности, появляющиеся у студентов со статистикой, по сути имеется неприятности ясного представления о взятых данных. Вводное знакомство со статистикой не выходит за рамки возможностей любого, кто достаточно разбирается в алгебре, дабы применять символы «плюс» и «минус», и подставлять числа вместо букв в уравнениях.
Описательная статистика
Статистика помогает в первую очередь для сокращенного описания громадных количеств данных. Предположим, нам нужно изучить показатели на вступительных экзаменах в колледж для 5000 обучающихся, записанные на карточках в регистратуре. Эти показатели являются сырыми данными. Перелистывание карточек вручную даст нам некое чувство о показателях обучающихся, но удержать все это в голове будет нереально. Исходя из этого мы делаем из этих данных собственного рода резюме, усредняя все показатели либо находя большую и минимальную величину. Эти статистические резюме облегчают обдумывание и запоминание данных. Такие резюмирующие высказывания именуют описательной статистикой.
Частотное распределение
Элементы сырых данных становятся постижимы, в то время, когда они сгруппированы в частотное распределение. Дабы сгруппировать эти, мы должны сперва поделить шкалу, по которой они измерялись, на промежутки, и после этого посчитать, сколько элементов приходится на любой промежуток. Промежуток, в котором группируются величины, именуется групповым промежутком. Ответ о том, на какое количество групповых промежутков нужно разбить эти, не определяется каким-либо правилом, а исходит от ответа исследователя.
В табл. П1 продемонстрирована выборка сырых данных, отражающих показатели 15 обучающихся на вступительных экзаменах в колледж. Показатели приведены в том порядке, в каком обучающиеся сдавали экзамен (у первого обучающегося показатель был 84, у второго — 61 и т. д.). В табл. П2 эти же эти представлены в виде частотного распределения, для которого групповой промежуток был установлен равным 10. На промежуток от 50 до 59 приходится один показатель, на промежуток от 60 до 69 — два и т. д. Увидьте, что большая часть показателей приходятся на промежуток от 70 до 79 и что ни один показатель не ниже промежутка 50-59 либо выше промежутка 90-99.
Таблица П1. Сырые показатели
84, 61, 72, 75, 77, 75, 75, 87, 79, 51, 91, 67, 79, 83, 69
(Показатели 15 обучающихся на вступительных экзаменах в колледж, приведенные в том порядке, в каком обучающиеся сдавали экзамен.)
Таблица П2. Частотное распределение
| Групповые промежутки | Число лиц в группе |
| 50-59 | |
| 60-69 | |
| 70-79 | |
| 80-89 | |
| 90-99 |
Показатели из табл. П1, разрушенные на групповые промежутки.
Частотное распределение легче осознать, в то время, когда оно представлено графически. Самый обширно используемая графическая форма — это частотная гистограмма; ее пример продемонстрирован в верхней части рис. П1. Гистограммы составляются методом рисования полос, основания которых задаются групповыми промежутками, а высота — соответствующими частотами групп. Еще один метод представления частотного распределения в графической форме — огибающая частоты, пример которой продемонстрирован в нижней части рисунка П1. При построении огибающей частоты групп отмечаются наоборот середины промежутка групп, а после этого эти точки соединяются прямыми линиями. Для завершения картины на каждом финише распределения добавляется еще один класс; потому, что у этих классов частота нулевая, оба финиша оказавшейся фигуры окажутся на горизонтальной оси. Огибающая частоты дает ту же данные, что и частотная гистограмма, но складывается из последовательности соединенных отрезков, а не из полос.
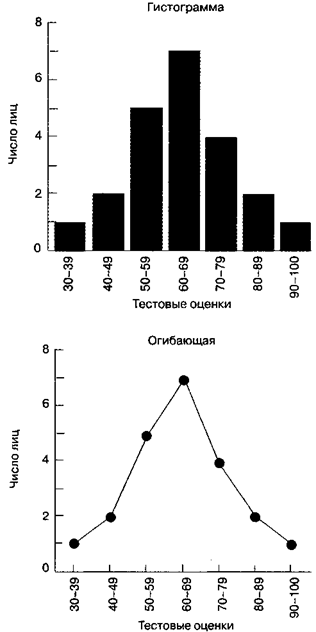
Рис. П1. Частотные графики.Тут отображены эти из табл. П2. Вверху — частотная гистограмма, внизу — огибающая частоты.
На практике число элементов получается значительно громадным, чем то, что отражено на рис. П1, но на всех картинках этого приложения продемонстрировано предельное число данных, так дабы вы имели возможность легко проверить этапы размещения в таблице и на графике.
Меры среднего
Мера среднего — это легко показательная точка на шкале, сжато отражающая изюминка имеющихся данных. В большинстве случаев употребляются три меры среднего: среднее значение, мода и медиана.
Среднее значение (либо легко среднее) — это привычное нам арифметическое среднее, получающееся при сложении всех размеров и делении взятой суммы на их количество. Сумма сырых размеров из табл. П1 равна 1125. В случае, если поделить ее на 15 (общее число размеров), то среднее будет 75.
Медиана — отметка среднего элемента последовательности, взятой методом размещения всех размеров по порядку и после этого отсчета к середине, начиная с любого финиша. В случае, если 15 размеров из табл. П1 расположить по порядку от самого громадного к самому малому 8-я величина с любого финиша будет равна 75. В случае, если исходное количество размеров будет четным, то мы среднее от тех двух, каковые оказываются в середине.
Мода — это самый довольно часто видящийся показатель в данной выборке. Самая нередкая величина в табл. П1 — это 75, следовательно, мода этого распределения равна 75.
При обычном распределении, в то время, когда величины распределены поровну с каждой стороны от середины (как на рис. П1), среднее, мода и медиана однообразны. Это не верно для скошенных, либо несимметричных, распределений. Предположим, нам нужно проанализировать времена отправления утреннего поезда. В большинстве случаев поезд отправляется одновременно с; случается, он отправляется позднее, но он ни при каких обстоятельствах не уходит раньше времени. У поезда с отправлением по расписанию в 08:00 время отправления на протяжении семи дней может оказаться таким:
Пн: 08:00
Вт: 08:04
Ср: 08:02
Чт: 08:19
Пт: 08:22
Сб: 08:00
Вс: 08:00
Это распределение времен отправления есть скошенным из-за двух запоздавших отправлений; они увеличивают среднее время отправления, но не очень сильно воздействуют на моду и медиану.
Принципиально важно осознать суть скошенного распределения, потому, что в противном случае отличие между средним и медианой время от времени тяжело уловить (рис. П2). В случае, если, к примеру, ее профсоюз и руководство фирмы спорят из-за благосостояния работников, средняя величина затрат на заработную плат и их медиана смогут сдвинуться в противоположных направлениях. Предположим, компания поднимает заработную плат практически всем сотрудников, но урезает заработную плат высшим управленцам, каковые были через чур высоко на шкале оплаты; тогда медиана заработной плата может встать вверх, в то время как средняя величина заработной плата снизится. Сторона, стремящаяся продемонстрировать, что заработная плат возросла, выберет в качестве индикатора медиану, а сторона, стремящаяся продемонстрировать понижение заработной плата, выберет среднее.
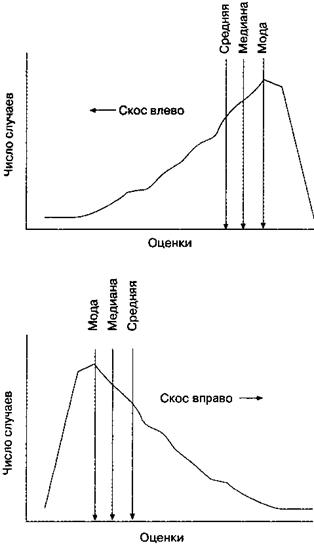
Рис. П2. Кривая скошенного распределения.Увидьте, что скос распределения имеет то направление, в котором спадает его хвост. Увидьте кроме этого, что у скошенного распределения среднее, мода и медиана не совпадают; медиана в большинстве случаев находится между средним и модой.
Меры вариации
В большинстве случаев, о распределении необходимо знать больше, чем смогут продемонстрировать меры среднего. Нужна, к примеру, мера, которая может сообщить, расположен ли пучок размеров близко к их среднему либо обширно разбросан. Мера разброса размеров относительно среднего именуется мерой вариации.
Показатель вариации нужен как минимум в двух отношениях. Во-первых, он показывает репрезентативность среднего. В случае, если вариация мала, то как мы знаем, что отдельные размеры будут близки к среднему. В случае, если вариация громадная, то такое среднее запрещено с громадной уверенностью применять в качестве репрезентативной величины. Предположим, что шьется партия готовой одежды без снятия конкретных мерок. Для этого полезно знать средний размер данной группы людей, вместе с тем принципиально важно знать и разброс их размеров. Зная вариацию, возможно сообщить, как должны варьироваться изготовляемые размеры.
Для иллюстрации взглянуть на эти рис. П3, где приведены частотные распределения показателей вступительных экзаменов для двух классов из 30 обучающихся. В обоих классах средний показатель одинаковый — 75, но они разумеется различаются по степени вариации. Показатели всех обучающихся из класса А расположены близко к среднему, в то время как показатели обучающихся из класса Б разбросаны в широком диапазоне. Необходимы какие-то меры, дабы правильнее выяснить, чем различаются эти распределения. Психологи довольно часто применяют три меры вариации: размах, стандартное отклонение и дисперсия.
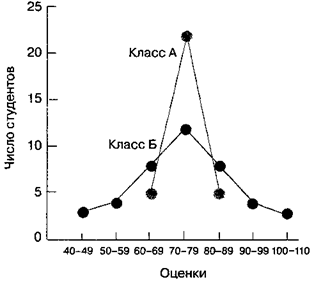
Рис. П3. Пример различной вариации распределений.Как легко видеть, пучок показателей у класса А ближе к среднему, чем показатели класса Б, не смотря на то, что само среднее в обоих классах аналогично — 75. У класса А все показатели попадают между 60 и 89, причем большая часть из них приходится на промежуток от 70 до 79. У класса Б показатели распределены довольно равномерно по всему диапазону от 40 до 109. Это различие между двумя распределениями в разбросе возможно оценить по показателю стандартного отклонения, которое у класса А меньше, чем у класса Б.
Дабы упростить арифметические вычисления, предположим, что пять обучающихся из каждого класса захотели поступить в колледж и что их суммарные оценки на вступительных экзаменах были такие:
Показатели обучающихся из класса А:
73, 74, 75, 76, 77 (среднее = 75)
Показатели обучающихся из класса Б:
60, 65, 75, 85, 90 (среднее = 75)
Сейчас подсчитаем для этих двух выборок меры вариации.
Размах — это разброс между наивысшей и наинизшей величиной. Размах показателей у пяти обучающихся из класса А равен 4 (от 73 до 77); размах показателей обучающихся класса Б равен 30 (от 60 до 90).
Размах легче подсчитать, но стандартное отклонение и дисперсия употребляются чаще. Это более чувствительные меры вариации, потому, что они учитывают все величины, а не только крайние размеры, как размах. Дисперсия показывает, как составляющие распределение величины отстоят от средней величины этого распределения. Дабы вычислить дисперсию, сперва подсчитаем отклонения каждой величины (d) от среднего, вычтя из среднего каждую величину (табл. П3). После этого нужно каждую отличие возвести в квадрат, дабы не было отрицательных чисел. Наконец, эти отклонения складываются совместно и делятся на общее число отклонений, давая в следствии средний квадрат отклонения. Средний квадрат отклонения именуется дисперсией. Проделав это с данными из рис. П3, мы найдём, что дисперсия у класса А равна 2,0, а у класса Б — 130. Разумеется, что у класса Б вариативность показателей существенно посильнее.
Таблица П3. Вычисление стандартного отклонения и дисперсии
Оценки Класса А (Среднее = 75)
| d | d2 | |
| 77-75 | ||
| 76-75 | ||
| 75-75 | ||
| 74-75 | -1 | |
| 73-75 | -2 |
Сумма d2 = 10
Дисперсия = среднее по d2 = 10 / 5 = 2,0
Стандартное отклонение (?) = = 1,4
Оценки Класса Б (Среднее = 75)
| d | d2 | |
| 90-75 | ||
| 85-75 | ||
| 75-75 | ||
| 65-75 | -10 | |
| 60-75 | -15 |
Сумма d2 = 650
Дисперсия = среднее по d2 = 650 / 5 = 130
Стандартное отклонение (?) = = 11,4
Неудобство дисперсии пребывает в том, что она выражена в единицах измерения, возведенных в квадрат. Исходя из этого величина дисперсии, равная 2 у класса А, не свидетельствует, что его усредненные показатели отличаются от среднего на 2 пункта. Она говорит о том, что 2 — это итог сглаживания возведенных в квадрат значений, на каковые показатели отличаются от среднего. Чтобы получить меру отклонения, выраженную в начальных единицах измерения (в этом случае это количество единиц, собранных на экзамене), нужно из дисперсии квадратный корень. Итог именуют стандартным отклонением. Оно обозначается греческой буквой ? (сигма), применяемой кроме этого в некоторых вторых статистических вычислениях, каковые мы обсудим кратко. Стандартное отклонение вычисляется по следующей формуле:
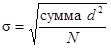
Пример вычисления стандартного отклонения.(табл. П3). Показатели выборок из двух классов представлены в виде, эргономичном для вычисления стандартного отклонения. На первой стадии вычитаем среднее из каждого показателя (среднее = 75 в обоих классах). В следствии приобретаем хорошие размеры d для показателей, каковые больше среднего, и отрицательные для тех, каковые меньше его. В то время, когда полученные размеры будут возведены в квадрат, символ минус пропадет (следующая колонка в табл. П3). Возведенные в квадрат разности складываются и делятся на N — количество элементов выборки, в нашем случае N = 5. Извлекая квадратный корень, приобретаем стандартное отклонение. [В этом ознакомительном изложении мы везде будем применять ? (сигма). Но в научной литературе для обозначения стандартного отклонения выборки употребляется маленькая буква s, а через а обозначают стандартное отклонение для всей группы. Помимо этого, при вычислении стандартного отклонения для выборки (s) сумма всех d2 делится не на N, а на N-1. При больших выборок, но, применение N-1 вместо N мало воздействует на величину стандартного отклонения. Для упрощения объяснений мы не будем различать тут группы и стандартное отклонение выборки и используем для них одну и ту же формулу. Обсуждение этого момента см. в: Phillips (1992).]
Статистические выводы
Сейчас, познакомившись со статистикой как методом описания данных, мы готовы обратиться к интерпретации данных — тому, как из них делают выводы.
выборки и Группа
В первую очередь, нужно различать выборку и группу из данной группы. Бюро переписи Соединенных Штатов пробует обрисовать население в целом методом получения описательного материала по возрасту, домашнему положению и т. д. обо всех обитателях страны. Слово несколько (population) годится для бюро переписи, потому, что оно воображает всех людей, живущих в Соединенных Штатах.
В статистике слово «несколько» не ограничено людьми, животными либо предметами. Группой смогут быть все величины температур, зарегистрированные термометром в течение последнего десятилетия, все слова английского либо каждый определенный запас данных. Довольно часто у нас нет доступа ко всей группе, и тогда мы пробуем представить ее по выборке, забранной в случайном (непредвзятом) порядке. Возможно задаться каким-либо вопросом о случайно отобранной части людей, как это сделало Бюро переписи в некоторых недавних переписях; возможно вывести среднюю температуру, снимая показания термометра в определенное время и не ведя постоянной записи; возможно оценить количество слов в энциклопедии, подсчитав слова на случайно выбранных страницах. Во всех этих примерах делается выборка из группы. В случае, если какие-либо из этих процессов повторить, результаты будут легко разны потому, что выборка не абсолютно отражает группу в целом и, следовательно, содержит неточности выборки. Конкретно тут вступают в игру статистические выводы.
Выборку данных из группы собирают, дабы сделать вывод об данной группе. Возможно изучить выборку данных переписи, дабы определить, стареет ли население, к примеру, и существует ли тенденция миграции в пригородные территории. Сходным образом, результаты экспериментов изучаются, дабы выяснить, какое действие экспериментальные манипуляции оказали на поведение — повлияла ли громкость на порог восприятия высоты звука, либо оказывают ли особенности воспитания значительное влияние на последующую судьбу. Дабы делать статистические выводы, нужно оценить отношения, на каковые показывают эти выборки. Такие выводы постоянно имеют некую степень неопределенности из-за неточностей выборки. В случае, если статистические опробования говорят о том, что величина результата, найденная в данной выборке, велика (относительно оценки неточности выборки), то возможно быть уверенным, что замечаемый в данной выборке эффект существует и у группы в целом.
Так, статистический вывод связан с необходимостью сделать вывод либо суждение довольно некоей характеристики группы, основываясь лишь на информации, взятой о выборке из данной группы. В качестве знакомства со статистическим выводом мы разглядим обычное его применение и распределение при интерпретации стандартного отклонения.
Обычное распределение
В то время, когда много данных собирают, воображают в табличном виде и отображают в виде гистограммы либо огибающей, они довольно часто образуют колоколообразное симметричное распределение, известное как обычное распределение. Большая часть его элементов находятся вблизи среднего (верхняя точка колокола), и данный колокол быстро спадает у самой большой и у самой малой величины. Такая форма кривой воображает особенный интерес, потому, что она появляется и тогда, в то время, когда итог процесса основан на множестве случайных событий, все из которых происходят независимо. Демонстрационное устройство, продемонстрированное на рис. П4, разрешает заметить, как из случайных событий складывается обычное распределение. Случайный фактор — упадет ли металлический шарик влево либо вправо любой раз, в то время, когда он попадает в развилку, — ведет к симметричному распределению: больше шариков падают прямо посередине, но иногда один из них достигает одного из крайних отделений. Это эргономичная визуализация того, что имеется в виду под случайным распределением, родным к обычному распределению.

Рис. П4. Устройство для демонстрации обычного распределения случайной величины.Устройство держат вверх ногами, пока все металлические шарики не скатятся в резервуар. После этого устройство переворачивают и держат вертикально, пока шарики, пройдя по полю со штырьками, не скатятся в 9 колонок-углублений внизу. Правильное количество шариков, попавших в каждую колонку, в различных демонстрациях будет неодинаковым. Но в среднем высота колонок из шариков будет приблизительно повторять обычное распределение, в то время, когда самая высокая колонка находится в центре, а высоты остальных колонок будут понижаться в направлении к краям.
Обычное распределение (рис. П5) — это математическое представление идеализованного распределения, приближенно создаваемого устройством, продемонстрированным на рис. П4. Обычное распределение показывает возможность того, что элементы в группе с обычным распределением будут различаться от среднего на любую заданную величину. В процентах на рис. П5 продемонстрирована часть площади, лежащей под кривой между указанными размерами шкалы; площадь под кривой соответствует группе в целом. Приблизительно две трети всех случаев (68%) попадают в промежуток между плюс и минус одним стандартным отклонением от среднего (±1?); 95% всех случаев — в промежуток ±2?; и фактически все случаи (99,7%) — в ±3?.
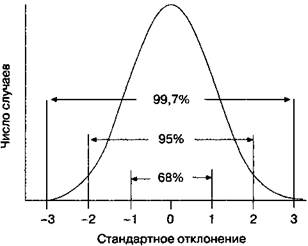
Рис. П5. Обычное распределение.Кривую обычного распределения возможно выстроить, применяя среднее и стандартное отклонение. Площадью под кривой, лежащей левее -3? и правее +3?, возможно пренебречь.
Более подробный перечень площадей под частями кривой обычного распределения приведен в табл. П4.
Таблица П4. Площадь участков под кривой обычного распределения как часть неспециализированной площади под ней
| Стандартное отклонение | (1) Площадь левого участка от данного значения | (2) Площадь правого участка от данного значения | (3) Площадь участка между данным значением и средней |
| -3,0 ? | 0,001 | 0,999 | 0,499 |
| -2,5 ? | 0,006 | 0,994 | 0,497 |
| -2,0 ? | 0,023 | 0,977 | 0,477 |
| -1,5 ? | 0,067 | 0,933 | 0,433 |
| -1,0 ? | 0,159 | 0,841 | 0,341 |
| -0,5 ? | 0,309 | 0,691 | 0,191 |
| 0,0 ? | 0,500 | 0,500 | 0,000 |
| +0,5 ? | 0,691 | 0,309 | 0,191 |
| +1,0 ? | 0,841 | 0,159 | 0,341 |
| +1,5 ? | 0,933 | 0,067 | 0,433 |
| +2,0 ? | 0,977 | 0,023 | 0,477 |
| +2,5 ? | 0,994 | 0,006 | 0,494 |
| +3,0 ? | 0,999 | 0,001 | 0,499 |
Давайте при помощи табл. П4 проследим, как получаются величины 68% и 95%, продемонстрированные на рис. П5. В табл. П4 в третьей колонке находим, что между -1? и средним лежит 0,341 неспециализированной площади и между +1? и средним также 0,341 неспециализированной площади. В сумме эти размеры дают 0,682, что на рис. П5 продемонстрировано как 68%. Сходным образом площадь от -2? до +2? составит 2 х 0,477 = 0,954, продемонстрированные как 95%.
Шкалирование данных
Дабы трактовать показатель, довольно часто необходимо знать, большой он либо низкий по отношению к вторым показателям. В случае, если человеку, сдающему водительский экзамен, требуется 0,500 сек, дабы надавить на тормоз по окончании сигнала опасности, как выяснить, скоро это либо медлительно? Вычислять ли, что студент сдал курс по физике, в случае, если его показатель на экзамене равен 60? Для ответа на такие вопросы нужно вывести шкалу, с которой эти показатели возможно сравнивать.
Ранжирование данных.Располагая показатели по рангу от большого к низкому, мы приобретаем одну из таких шкал. Отдельный показатель интерпретируется по тому, на каком месте он находится среди группы показателей. К примеру, курсанты военной академии Вест Пойнт знают, где они находятся в собственном классе — быть может, 35-ми либо 125-ми в классе из 400.
Обычный показатель.Стандартное отклонение — эргономичная единица шкалирования, потому, что мы можем оценить, как на большом растоянии от среднего находятся 1? либо 2? (табл. П4). Величину произведения, в котором один сомножитель — стандартное отклонение, именуют стандартным показателем. Многие шкалы, используемые в психотерапевтических измерениях, основаны на принципе стандартного показателя.
Пример вычисления стандартного показателя.В табл. П1 приведены показатели, полученные 15 студентами на вступительных экзаменах. Не имея дополнительной информации, мы не знаем, являются ли эти показатели репрезентативными для группы всех поступавших. Но предположим, что средний показатель на этих экзаменах был 75, а стандартное отклонение 10.
Каким же будет обычный показатель у студента, собравшего на экзаменах 90 баллов? Как выше среднего лежит данный показатель, нужно выразить числом стандартных отклонений:
Обычный показатель для студента, с оценкой 90 равен:
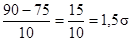
В качестве второго примера заберём обучающегося с оценкой 53.
Обычный показатель для оценки 53 равен:
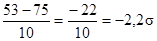
В этом случае показатель обучающегося лежит ниже среднего на 2,2 стандартных отклонения. Так, символ стандартного показателя (+ либо -) говорит о том, выше либо ниже среднего находится этот показатель, а его величина показывает, как на большом растоянии от среднего он находится в единицах стандартных отклонений.