Представление оператора в матричной форме

A=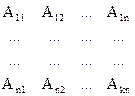

Совокупность коэффициентов Akn, представленная в виде таблицы, имеется матричное представление оператора.

Главные операторы квантовой механики

1. Оператор кинетической энергии

Кинетическая энергия равна:

T=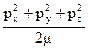

Оператор кинетической энергии имеет форму:

=

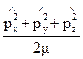
С учетом оператора импульса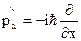

и оператора квадрата импульса ,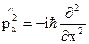

где .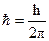

Оператор кинетической энергииимеет вид:

=

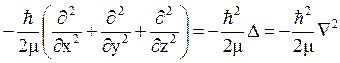
2. Оператор момента импульса

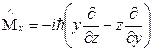
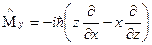
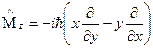
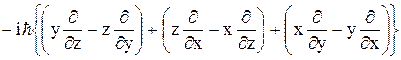
3. Оператор квадрата момента импульса

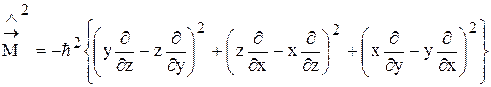
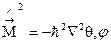
4. Оператор Гамильтона (гамильтониан)

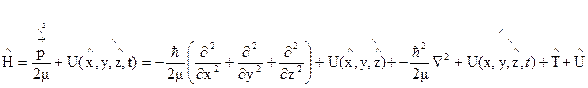
5. Оператор Гамильтона для совокупности не взаимодействующих частиц

,

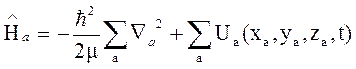где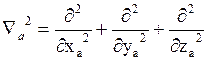

6. Оператор Гамильтона для совокупности взаимодействующих

частиц

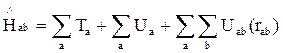
где — сумма кинетических энергий,

— потенциал внешнего поля,

— потенциал сотрудничества двух частиц.

,

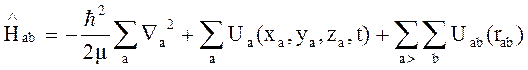Операторная алгебра употребляется при ответе уравнения Шредингера – главного уравнения, которое лежит в базе всей квантовой механики и квантовой химии.

Использованный Эйнштейном для описания фотоэлектрического результата подход потребовал, дабы квант электромагнитного излучения (что он назвал фотоном) владел связанным с ним импульсом. В 1925 г. Луи де Бройль исходил из предположения, что в случае, если при определенных событиях электромагнитное излучение может владеть особенностями частиц, а не волн, то вероятны события, при которых частицы вещества должны владеть волновыми особенностями.

Применяя соотношение и уравнение Эйнштейна Планка, де Бройль доказал, что каждая частица вещества владеет волновыми особенностями.

Приравняв эти два соотношения по энергии, возьмём

E=mc2 E=hn=

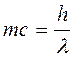
Заменив скорость света на скорость любой частицы, направляться записать

mU либо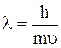

В 1924 г. Луи де Бройль внес предложение распространить корпускуляр-но-волновые представления на все микрочастицы, т.е. перемещение любой микрочастицы разглядывать как волновой процесс. Математически это отыскало выражение в соотношенииде Бройля, в соответствии с которому частице, имеющей массу m и движущейся со скоростью u, соответст-вует волна длиной l.

Догадка де Бройля была экспериментально подтверждена обнару-жением у потока электронов дифракционного и интерференционного эффектов. На данный момент дифракция потоков электронов, нейтро-нов, протонов обширно употребляется для изучения структуры веществ.

В соответствии с соотношению де Бройля, с перемещением электронов (масса 9,1 . 10 –31 кг, скорость порядка 106 м/с) ассоциируется волна длиной порядка 10 –10 м, т.е. ее протяженность соизмерима с размерами атомов. Исходя из этого при рассеянии электронов кристаллами отмечается дифракция, причем кристаллы делают роль дифракционной решетки.

С перемещением макрочастиц, напротив, ассоциируется волна столь малой длины (10 –29 м и меньше), что экспериментально волновой процесс найти не удается.

Волновая природа вещества была подтверждена Девиссоном и Джермером, каковые продемонстрировали, что пучок электронов может дифрагироваться иногда расположенными атомами кристалла.

Из соотношения де Бройля направляться условие квантования Бора для орбитального момента. В случае, если электрон на орбите в модели Бора владеет волновыми особенностями, то на орбите обязана образовываться стоячая волна, т.е. протяженность орбиты должна быть целочисленно кратна длины волны, в противном случае интерференция уничтожит орбиту. Это значит, что протяженность волны прямо пропорциональна радиусу орбиты

2pr = nl либо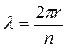

Импульс частицы возможно вычислить по уравнению

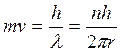
Из этого можно взять условие квантования Бора

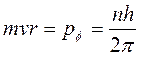
Шредингер развил собственную волновую механику, исходя из волновых уравнений хорошей теории электромагнитного излучения и подставив в них соотношение де Бройля.

Волновая функция

Уравнение Максвелла, обрисовывающее распостранение волны в одном измерении, имеет форму

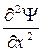
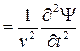
где Y — функция, обрисовывающая волну (волновая функция), x – направление распостранения волны, U –скорость распостранения волны, t – время.

самоё общее ответ этого дифференциального уравнения имеет форму

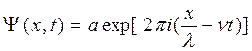
где a – амплитуда.

Ответ возможно записать в виде

Обозначим aexp(2pix/l) как y(x). Тогда

Продифференцировав это выражение по x, находим

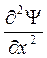
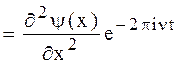
Дифференцируя полученный итог по времени, возьмём следующее выражение

=

а по окончании повторного дифференцирования по времени возьмём уравнение:

=

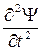Подстановка вторых производных волновой функции по координате и времени в исходное уравнение ведет к соотношению

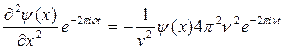
Уменьшая экспоненциальные члены и приравнивая n2/U2 к l-2, приобретаем

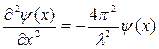
В случае, если подставить в это уравнение вместо длины волны соотноше-ние де Бройля, то окажется

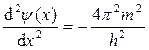U2y(x)

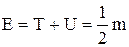U2 + U

U2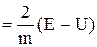

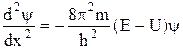
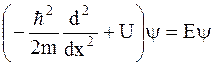
= Ey

В последнем уравнении мы перешли к полному дифференциалу, т.к. функция y есть функцией одной переменной.

Классическая механика и электродинамика при попытке применить их объяснению ядерных явлений, как об этом говорилось ранее, приводи-ли к итогам, находящихся в резком несоответствии с опытом. самый яркий тому пример — попытка применения хорошей электродинамики к модели атома, в которой электроны движутся около ядра по хорошим орбитам. При таком перемещении, как и при всяком перемещении зарядов с ускорением, электроны должны были бы непрерывно излучать энергию в виде электромагнитных волн и в итоге — неизбежно упасть на положительно заряженное ядро. Так, с позиций хорошей электродинамики — атом неустойчив. Как мы видим данный тезис не соответствует действительности. Такое глубокое несоответствие теории с опытом говорит о том, что описа-ние микрообъектов требует фундаментального трансформации в главных законах и классических представлениях.

Из многих экспериментальных данных (таких, как дифракция электронов) направляться, что механика, которой подчиняются ядерные явления — квантовая механика — должна быть основана на представлениях о перемещении, принципиально хороших от представлений классической механики. В квантовой механике не существует понятия траектории частиц, следовательно — и других динамических черт.

Данный тезис сформулирован в принципе неопределенности Гейзенберга, что говорит, что динамические переменные, характеризующие совокупность, смогут быть поделены на две (взаимно дополнительные) группы: 1) временные и пространственные координаты (t и q); 2) энергия и импульсы (p и E).

Запрещено со сколь угодной точностью в один момент измерить импульс и пространственную координату (либо энергию микрообъекта и временную координату), что отражено в соотношении неопределен-ностей

Dq·Dp ³ либо

Dt·DE ³ ,

где Dq,·Dp, Dt,·DE – неопределенности координаты, импульса, времени и энергии соответственно.

Это связано не с ограниченной разрешающей свойством устройств, а отражает основной закон природы.

Соотношения неопределенностей содержат в правой части постоянную Планка, величина которой сравнима с другими энергетически-ми чертями в том случае, если исследуются совокупности, складывающиеся из маленького числа частиц. При изучении макроскопических тел выясняется значимой величина порядка 10-7 Дж, в таких случаях величиной h возможно пренебречь, т.е. вычислять h=0. В случае, если h=0, то выясняются применимыми законы классической механики.

Соотношения неопределенностей нельзя вывести и строго доказать, их справедливость определяется отсутствием исключений из них. Воздействие принципа неопределенности проявляется во всем устройстве окружающего нас мира. С его помощью легко ответить на вопрос о том, по какой причине электрон в атоме не падает на ядро. Если бы электрон упал на ядро, то его положение было бы известно с точностью, соответствующей размеру ядра, т.е. приблизительно 10-13 см. Неопределенность импульса равна Dp=h/Dq=1,054 г.см/с, а неопределенность кинетической энергии электрона DEк=Dp2/2me=3,81.1010 эВ. Такая величина кинетической энергии существенно превышает энергию электронов в атоме, которая, к примеру, для водорода образовывает 13,6 эВ. Электрон с таковой энергией покинет атом.

Колебания атомов и ионов в кристаллической решетке либо молекуле, совершающиеся кроме того при полном нуле, кроме этого являются следствием принципа неопределенности, т.к. при их отсутствии было бы известно совершенно верно положение атомов либо ионов (геометрические характеристики кристаллической решетки смогут быть выяснены совершенно верно).

Как мы знаем, что полное описание состояния хорошей физической совокупности осуществляется заданием в начальный момент времени всех ее скоростей и координат. Согласно этой информации уравнения перемещения абсолютно определяют поведение совокупности во времени. В квантовой механике, потому, что координаты и соответствующие им скорости не существуют в один момент, описание осуществляется меньшим числом размеров, т.е. есть менее подробным. Конкретно исходя из этого квантовая механика не имеет возможности делать строго определенных предсказаний довольно будущего поведения микрообъекта, и ее задача состоит только в определении возможности получения того либо иного результата при измерении.

Конечно, что столь радикальное изменение физических представ-лений о перемещении требует и столь же радикального трансформации математического аппарата.

Правила квантовой механики

Принцип №1. Состояние частицы (либо совокупности частиц) задано, в случае, если известна функция y(q1, q2, …, qn, t) от координат всех образующих совокупность частиц и времени, именуемая функцией состояния совокупности либо волновой функцией.

В квантовой механике состояние всей совокупности возможно обрисовано функцией координат y(q), квадрат модуля которой определяет распределе-ние возможностей значений координат:

|y (q)|2dq

— имеется возможность того, что произведенное над совокупностью измерение найдёт значение координат в элементе количества dq. Функцию y(q) именуют волновой функцией совокупности. Волновая функция обязана удовлетворять последовательности требований:

• Она должна быть постоянной.
• Она должна быть однозначной.
• Она должна быть интегрируема с квадратом, т.е. интеграл o|y(q)|2dq обязан существовать.
• Она должна быть нормированной, т.е. данный интеграл должен быть равен 1.

Вероятностный суть волновой функции ведет к следующему ее свойству: возможность отыскать частицу в любом элементе количества не должна обращаться в бесконечность. Довольно часто это сводится к требованию, дабы сама функция не обращалась бы в бесконечность.

Физический суть последнего утверждения достаточно несложен и прозрачен: сумма возможностей всех вероятных значений координат равна единице, поскольку обнаружение объекта в любой точке пространства — имеется событие точное.

направляться также подчернуть, что волновая функция совокупности возможно комплексной, и она выяснена только с точностью до фазового множителя exp(ia), где a — вещественное число. Эта неопределенность не может быть устранена, но она несущественна и не отражается на физических итогах.

Принцип № 2. Волновые функции подчиняются принципу суперпозиции: в случае, если в состоянии с волновой функцией y1(q) некое измерение ведет к результату Х1, а в состоянии y2(q) — к результату Х2, то любая функция вида y = с1y1(q)+с2y2(q) обрисовывает такое состояние, в котором измерение дает или итог Х1, или Х2.

Принцип № 3. Всякой физической величине L в квантовой механике сопоставлен линейный самосопряженный оператор. Единственно воз-можными размерами, каковые может иметь эта физическая величина, являются личные значения L операторного уравнения y =Ly.

Принцип № 4. Вероятная волновая функция состояния совокупности получается при ответе дифференциального уравнения

,

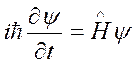где — оператор Гамильтона, а уравнение именуется уравнением Шредингера. Это уравнение не может быть выведено, оно постулировано Э. Шредингером в 1926 г.

Принцип № 5. В случае, если произвести многократные измерения какой-либо динамической переменной L совокупности, находящейся в состоянии y, то на основании результатов этих измерений возможно выяснить ее среднюю величину.

Эта средняя величина вычисляется по формуле:

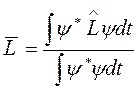— отношение Релея.

Интегрирование проводится по всем значениям координат и спинов, от которых зависит функция y, т.е. по x1, y1, z1, s1, …, xN, yN, zN, sN. Потому, что s принимает дискретные значения, интегрирование по поясницам s практически сводится к суммированию, но в неспециализированных формулах сохраняется символ интеграла, что свидетельствует, что проводится интегри-рование по координатам и суммирование по поясницам.

Либо среднее значение возможно обозначено следующим образом: . Последнее обозначение введено П. Дираком.

Проводя измерение черт микрообъектов, как правило нельзя пренебречь влиянием измерения на их состояние. К примеру, определяя энергию электрона в атоме, возможно ее изучить при сотрудничестве атома со световой волной. Но при таком сотрудничестве энергия атома изменится, и электрон окажется в другом состоянии. При повторном измерении энергии мы возьмём второе состояние. Чтобы проводить «многократные измерения», необхо-димо любой раз возвращать атом в исходное состояние. В действии-тельности, возврат данной частицы в начальное состояние – задача сложная, но в этом нет необходимости, т.к. все однообразные частицы тождественны. Исходя из этого достаточно иметь довольно много однообразных частиц в однообразных состояниях и попеременно проводить над ними измерения.

Принцип № 6.Волновая функция совокупности микрочастиц с полуцелым поясницей (в частности, электронов) должна быть антисим-метрична относительно перестановки координат любых двух частиц:

Y(q1, q2,…, qn)= -Y(q1, q2,…, qn)

Антисимметрия волновой функции электронов вытекает из их тождественности (неразличимости), т.е. из неосуществимости различить отдельные электроны атома, молекулы в любом опыте. Данный постулат был введен В. Паули в 1925 г.

Из всех операторов, видящихся в квантовой механике, главным есть оператор Гамильтона, гамильтониан:

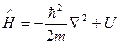
и определяет значение полной энергии совокупности. При, в то время, когда гамильтониан очевидно не зависит от времени, задача о его собственных значениях и собственных функциях сводится к уравнению

,

которое именуется стационарным уравнением Шредингера.

Из всех элементов периодической совокупности лишь его изотопы и водород относятся к одноэлектронным атомам, но рассмотрение совокупностей этого типа имеет фундаментальное значение, т.к. лишь для атомов и ионов с одним электроном (водородоподобных атомов) возможно совершенно верно решено уравнение Шредингера, а полученные ответы являются базой для изучения более непростых задач о молекулах и многоэлектронных атомах.

Перейдем к рассмотрению уравнения Шредингера.

Уравнение Шредингера

Эта задача имеет правильное аналитическое ответ, и его возможно взять в как в гейзенберговском, так и в шредингеровском представ-лении. Разглядим подход Шредингера. Атом водорода складывается из одного ядра и электрона. Заряд электрона равен –е. Пускай ядро имеет заряд +ze, где z-ядерный номер.

Потенциальная энергия U(r) одноэлектронного атома есть энергией кулоновского сотрудничества и функцией лишь расстояния между электроном и ядром.

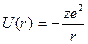
Разглядим перемещение электрона около неподвижного ядра, несложный случай перемещения частицы в центральном поле. Не учитывая спинового момента электрона гамильтониан совокупности возможно записать в виде

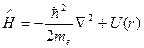
При перемещения электрона около ядра уравнение Шредингера выглядит так

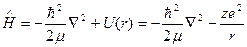
Оно есть более корректным, потому, что в этом выражении m -приведенная ядра и масса электрона, а не просто масса электрона, поскольку при перемещении электрона ядро пара смещается относительно центра весов совокупности. Если бы в гамильтониане употреблялась легко масса электрона, то это привело бы к значению энергии, содержащему погрешность в 0,05 %.

В связи с тем, что кулоновский потенциал сферически симмет-ричен (зависит лишь от расстояния между сферическими частицами), задачу целесообразно решать в сферических координатах, каковые связаны с декартовыми:

x=rsinqcosj

y=rsinqsinj

z=rcosq

dV=dxdydz= r2sinqdqdjdr,

где dV – элемент количества.

Рис.5.2. Сферическая и декартова совокупность координат

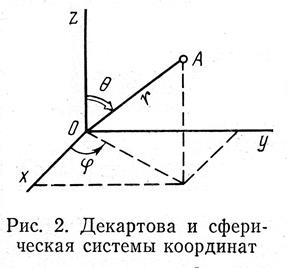
Переход к сферическим координатам позволяет разделения переменных, что нереально сделать при записи этого уравнения в декартовых координатах.

В сферических координатах оператор Лапласа принимает вид

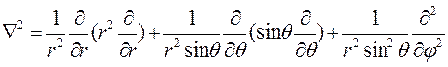
Подставив лапласиан и гамильтониан в уравнение Шредингера, возьмём

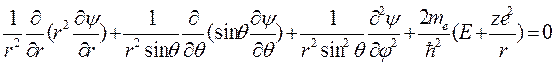
Дифференциальное уравнение в частных производных возможно решить, поделив переменные

Y(r, q, j)=R(r)Q(q)F(j)

Подставив полученное выражение в уравнение Шредингера и умножая его на 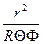, возьмём

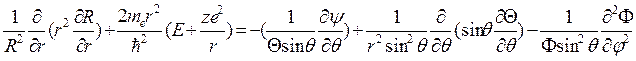
По окончании нужных преобразований, возьмём три уравнения.

Ответ F-уравнения

Ответом F-уравнения будет функция вида

F=Ae±imj,

то есть A=1/

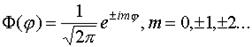
Ответ Q-уравнения

уравнения и-Решение возможно отыскать, применяя полиномы Лежандра.

Это уравнение имеет конечные ответы лишь в том случае, если выполняются условия

С=l(l+1), l=0, 1, 2… -l?m?l,

наряду с этим ответами являются полиномы Лежандра.

Нормированные функции Q имеют вид

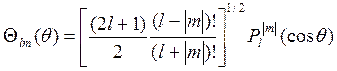
Присоединенные полиномы Лежандра имеют вид

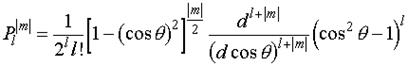
Вид функций Ql, m для разных значений l

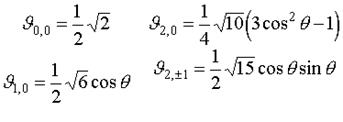
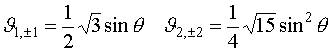
Произведение Q(q)F(j) представляет собой угловую часть волновой функции и именуется сферической гармоникой:

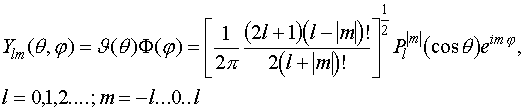
Так, ответами уравнения являются полиномы Лежандра, зависящие от характеристических чисел l и m (легко заметить, что эти числа имеется ни что иное, как орбитальное и магнитное квантовые числа электрона в атоме.

Ответ R-уравнения

Будем сейчас решать уравнение, зависящее от координаты

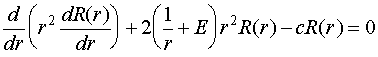
В случае, если в это уравнение подставить уже отысканное ранее значение константы 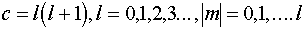, продиффиренциро-вать его в явном виде, первое слагаемое и после этого итог поделить на , то мы возьмём равенство

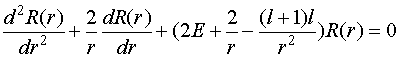
Ответ этого уравнения кроме этого направляться искать в виде последовательности по степеням :

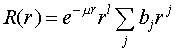
Тут 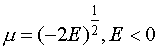и — численные коэффициенты.

По окончании подстановки возьмём:

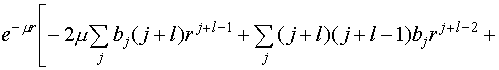
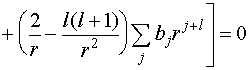
Разумеется, что данное уравнение справедливо только в том случае, лишь в случае, если выражение в квадратных скобках равняется нулю при любых , а это со своей стороны выполняется ли тогда, в то время, когда равны нулю суммы коэффициентов при однообразных степенях . Из этого следует рекуррентное соотношение для коэффициентов :

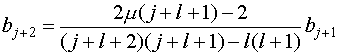
Функция в силу особенностей волновой функции должна быть конечной при любых , т.е. последовательность 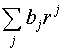обязан сходиться. Сравним данный последовательность с отлично известным разложением экспоненты :

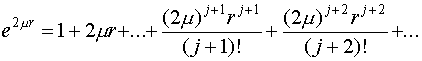
Отношение двух соседних участников этого последовательности равняется в предположении громадных :

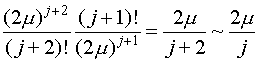
Но отношение двух соседних коэффициентов последовательности

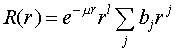при громадных также равняется ,

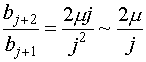т.е. последовательность 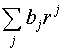близок к функции , что разрешает записать функцию R(r) в виде:

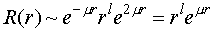
При функция в этом уравнении пытается к бесконечности, исходя из этого, чтобы удовлетворить условию конечности волновой функции при любых нужно оборвать последовательность, т.е. для некоего должно выполнятся условие 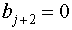, либо

Обозначив , мы возьмём связь между и

Сейчас, подставив вместо m его значение 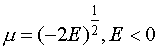и учитывая, как l зависит от n,мы сразу же возьмём выражение для энергии водородоподобного атома в ядерных единицах:

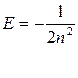либо в единицах СИ 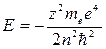, которое абсолютно сходится с формулой Бора.

Итак, ответ для радиальной части волновой функции с условием нормировки запишется как

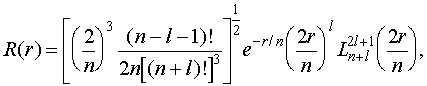
где 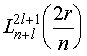— присоединенный полином Лягерра, что в явном виде равен

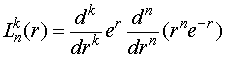
Для низших значений чисел и присоединенные полиномы Лягерра будут иметь следующий вид:

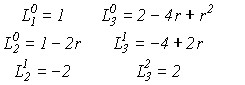
Ответ радиального уравнения Шредингера представляет собой нормированные функции

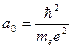
Посмотрим, какими смогут быть радиальные волновые функции:

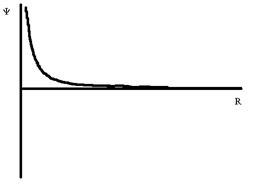1s	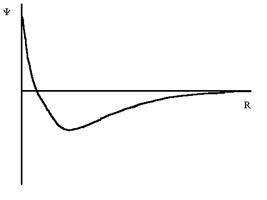2s
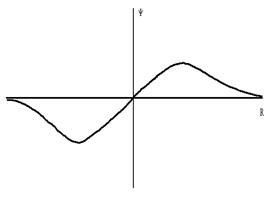2p	3s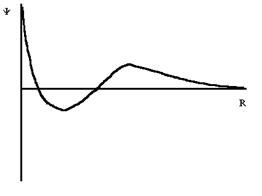
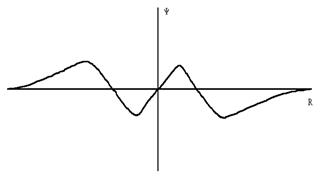3p	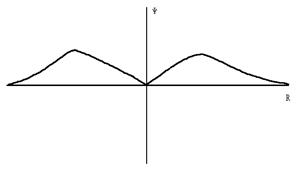3d

В целом возможность нахождения электрона в какой-либо точке пространства определяется как радиальной, так и угловой частями ядерной орбитали.

В вычислительных задачах квантовой химии вариационный способ практически в любое время используется для получения энергии и волновых функций главного состояния. С его помощью довольно часто удается конкретно взять энергии и волновые функции определенных возбужденных состояний, в случае, если предварительно заданы мультиплетность и симмет-рия. Теорию возмущений в большинстве случаев несложнее применять в задачах, требую-щих лишь качественных ответов. Помимо этого, для задач, к каким неприменим вариационный подход, теория возмущений может служить единственным средством ответа. В будущем мы столкнемся с проблемами, каковые подпадают под все эти категории. Одним из крайне важных применений теории возмущений являются зависящие от времени задачи, потому, что вариационный способ, в том виде, как мы его изложили выше, возможно применен лишь к стационарным состояниям.

Действие линейного оператора в матричной форме. Тема

Интересные записи:

• Применение методов поиска оптимального решения и нечеткой логики в экономических задачах
• Применение метода динамического программирования при принятии решений об оптимальном распределений инвестиций.
• Принципы международного сотрудничества в области охраны окружающей среды
• Принципы объектно-ориентированного программирования