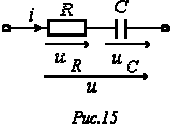
Опуская промежуточные выкладки, с применением соотношений (2) и (4) для ветви на рис. 15 возможно записать
| . , | (8) |
где
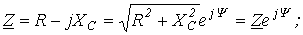
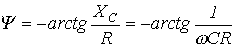, причем пределы трансформации 
.
|
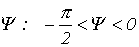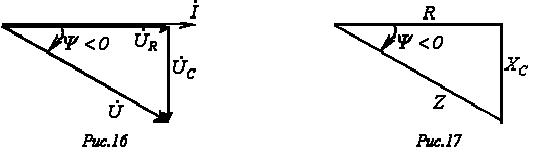
На основании уравнения (7) смогут быть выстроены треугольники напряжений (см. рис. 16) и сопротивлений (см. рис. 17), каковые являются подобными.
Параллельное соединение резистивного и емкостного элементов
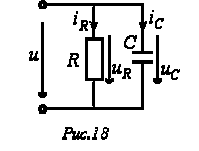
Для цепи на рис. 18 имеют место соотношения:
;
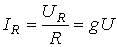, где 
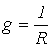[См] – активная проводимость;
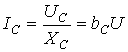, где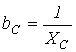 
[См] – реактивная проводимость конденсатора.
|
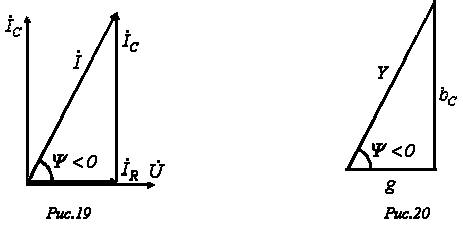
Векторная диаграмма токов для данной цепи, именуемая треугольником токов, приведена на рис. 19. Ей соответствует уравнение в комплексной форме
,
где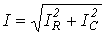 
;
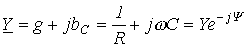— комплексная проводимость;
.
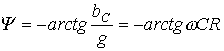Треугольник проводимостей, подобный треугольнику токов, приведен на рис. 20.
Для комплексного сопротивления цепи на рис. 18 возможно записать
.
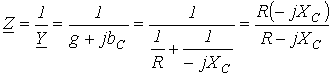Нужно подчернуть, что полученный итог подобен известному из курса физики выражению для эквивалентного сопротивления двух параллельно соединенных резисторов.
Параллельное соединение резистивного и индуктивного элементов
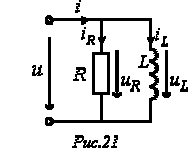
Для цепи на рис. 21 возможно записать
;
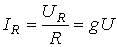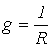, где [См] – активная проводимость;
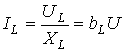, где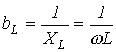 
[См] – реактивная проводимость катушки индуктивности.
Векторной диаграмме токов (рис. 22) для данной цепи соответствует уравнение в комплексной форме
,
где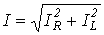 
;
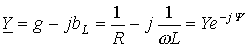— комплексная проводимость;
.
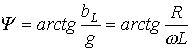Треугольник проводимостей, подобный треугольнику токов, приведен на рис. 23.
|
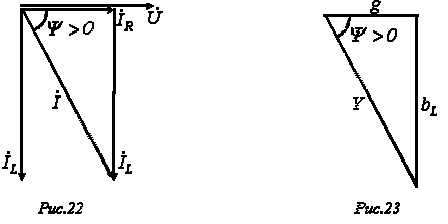
Выражение комплексного сопротивления цепи на рис. 21 имеет форму:
.
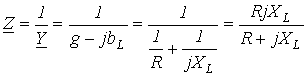Литература
1. Базы теории цепей: Учеб. для институтов /Г.В.Зевеке, П.А.направляться, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
2. Бессонов Л.А. Теоретические базы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных профессий институтов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
задачи и Контрольные вопросы
1. В чем сущность реактивных сопротивлений?
2. Какой из элементов: резистор, катушку индуктивности либо конденсатор – возможно применять в качестве шунта для наблюдения за формой тока?
3. По какой причине катушки индуктивности и конденсаторы не употребляются в цепях постоянного тока?
4. В ветви на рис. 12 . Выяснить комплексное сопротивление ветви, в случае, если частота тока .
Ответ: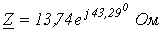 
.
5. В ветви на рис. 15 . Выяснить комплексное сопротивление ветви, в случае, если частота тока .
Ответ: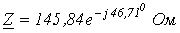 
.
6. В цепи на рис. 18 . Выяснить комплексные сопротивление и проводимость цепи для .
Ответ: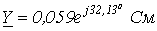 
; 
.
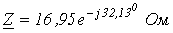7. Протекающий через катушку индуктивности ток изменяется по закону А. Выяснить комплекс действующего значения напряжения на катушке.
Ответ: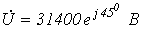 
.
|
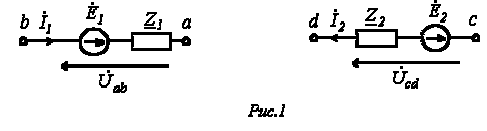
Заберём два участка цепи a-b и c-d (см. рис. 1) и составим для них уравнения в комплексной форме с учетом указанных на рис. 1 хороших направлений напряжений и токов.
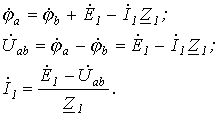
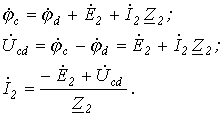
Объединяя оба случая, возьмём
|
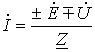
(1) |
либо для постоянного тока
 . |
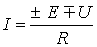(2) |
Формулы (1) и (2) являются аналитическим выражением закона Ома для участка цепи с источником ЭДС, в соответствии с которому ток на участке цепи с источником ЭДС равен алгебраической сумме напряжения на зажимах участка цепи и ЭДС, дроблённой на сопротивление участка. При переменного тока все указанные размеры сущность комплексы. Наряду с этим ЭДС и напряжение берут со знаком “+”, в случае, если их направление сходится с выбранным направлением тока, и со знаком “-”, в случае, если их направление противоположно направлению тока.
Базы символического способа расчета цепей
синусоидального тока
Расчет цепей переменного синусоидального тока может производиться не только методом построения векторных диаграмм, но и аналитически – методом операций с комплексами, символически изображающими синусоидальные ЭДС, напряжения и токи. Преимуществом векторных диаграмм есть их наглядность, недочётом – малая точность графических построений. Использование символического способа разрешает создавать расчеты цепей с громадной степенью точности.
Символический способ расчета цепей синусоидального тока основан на законах Кирхгофа и законе Ома в комплексной форме.
Уравнения, высказывающие законы Кирхгофа в комплексной форме, имеют совсем такой же вид, как и соответствующие уравнения для цепей постоянного тока. Лишь токи, ЭДС, напряжения и сопротивления входят в уравнение в виде комплексных размеров.
1. Первый закон Кирхгофа в комплексной форме:
| . | (3) |
2. Второй закон Кирхгофа в комплексной форме:
| (4) |
либо применительно к схемам замещения с источниками ЭДС
| . | (5) |
3. Соответственно матричная запись законов Кирхгофа в комплексной форме имеет форму:
§ первый закон Кирхгофа:
| . ; | (6) |
§ второй закон Кирхгофа
| . | (7) |
Пример.
Дано:
|
|
|
|
||
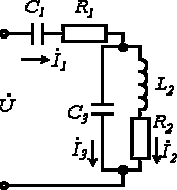
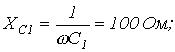
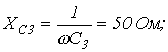
| Выяснить: | 1) полное комплексное сопротивление цепи ; | |
| 2) токи | ||
| Рис. 2 |
Ответ:
1. .
2. 
.
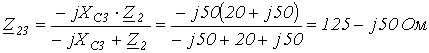3.
.
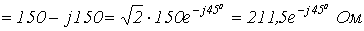4. Принимая начальную фазу напряжения за нуль, запишем:
.
Тогда
.
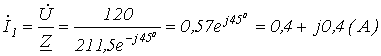5. Потому, что ток распределяется обратно пропорционально сопротивлению ветвей (это вытекает из закона Ома), то
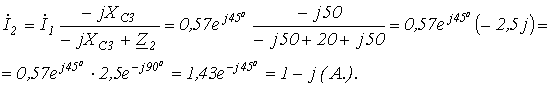
6. .
7. Подобный итог возможно взять, составив для данной схемы уравнения по законам Кирхгофа в комплексной форме
|
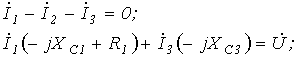
либо по окончании подстановки численных значений параметров схемы
Особые способы расчета
Режим работы любой цепи абсолютно характеризуется уравнениями, составленными на основании законов Кирхгофа. Наряду с этим нужно составить и решить совокупность с n малоизвестными, что может оказаться очень трудоемкой задачей при солидном числе n ветвей схемы. Но, число уравнений, подлежащих ответу, возможно сокращено, в случае, если воспользоваться особыми способами расчета, к каким относятся способы контурных токов и узловых потенциалов.
Способ контурных токов
Мысль способа контурных токов: уравнения составляются лишь по второму закону Кирхгофа, но не для настоящих, а для мнимых токов, циркулирующих по замкнутым контурам, т.е. при выбора основных контуров равных токам ветвей связи. Число уравнений равно свободных контуров, т.е. числу ветвей связи графа . Первый закон Кирхгофа выполняется машинально. Контуры возможно выбирать произвольно, только бы их число было равняется и дабы любой новый контур содержал хотя бы одну ветвь, не входящую в прошлые. Такие контуры именуются свободными. Их выбор облегчает применение топологических ветвей связи и понятий дерева.
Направления подлинных и контурных токов выбираются произвольно. Выбор хороших направлений перед расчётом может не определять настоящие направления токов в цепи. В случае, если в следствии расчета какой-либо из токов, как и при применении уравнений по законам Кирхгофа, окажется со знаком “-”, это указывает, что его подлинное направление противоположно.
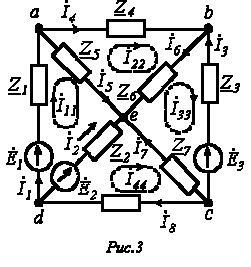Пускай имеем схему по рис. 3.
Выразим токи ветвей через контурные токи:
;
; ;
; .
Обойдя контур aeda, по второму закону Кирхгофа имеем
.
Потому, что ,
то
.
Так, взяли уравнение для первого контура довольно контурных токов. Подобно возможно составить уравнения для второго, четвёртого контуров и третьего:
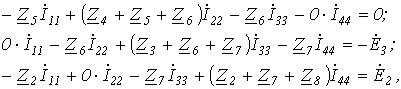
совместно с первым решить их довольно контурных токов и после этого по уравнениям, связывающим токи ветвей и контурные токи, отыскать последние.
Но эта совокупность уравнений возможно составлена формальным методом:
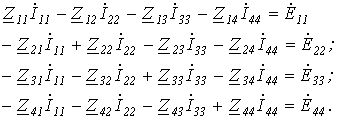
При составлении уравнений нужно не забывать следующее:
— сумма сопротивлений, входящих в i-й контур;
— сумма сопротивлений, неспециализированных для i-го и k-гоконтуров, причем ;
члены на основной диагонали постоянно пишутся со знаком “+”;
символ “+” перед остальными участниками ставится , если через неспециализированное сопротивление i-й и k- й контурные токи проходят в одном направлении, в другом случае ставится символ “-”;
в случае, если i-й и k- й контуры не имеют неспециализированных сопротивлений, то ;
в правой части уравнений записывается алгебраическая сумма ЭДС, входящих в контур: со знаком “+”, в случае, если направление ЭДС сходится с выбранным направлением контурного тока, и “-”, если не сходится.
В нашем случае, для первого уравнения совокупности, имеем:
направляться обратить внимание на то, что, потому, что , коэффициенты контурных уравнений в любой момент симметричны довольно основной диагонали.
В случае, если в цепи находятся кроме источников ЭДС источники тока, то они учитываются в левых частях уравнений как узнаваемые контурные токи: k- й контурный ток, проходящий через ветвь с k- м источником тока равен этому току .
Способ узловых потенциалов
Этот способ вытекает из первого закона Кирхгофа. В качестве малоизвестных принимаются потенциалы узлов, по отысканным значениям которых посредством закона Ома для участка цепи с источником ЭДС после этого находят токи в ветвях. Потому, что потенциал – величина относительная, потенциал одного из узлов (любого) принимается равным нулю. Так, число малоизвестных потенциалов, а следовательно, и число уравнений равняется , т.е. числу ветвей дерева .
Пускай имеем схему по рис. 4, в которой примем .
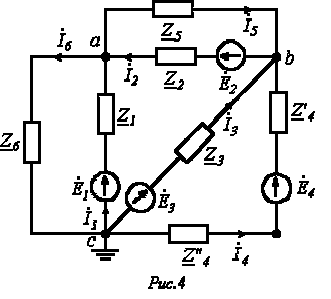Допустим, что и известны. Тогда значения токов на основании закона Ома для участка цепи с источником ЭДС
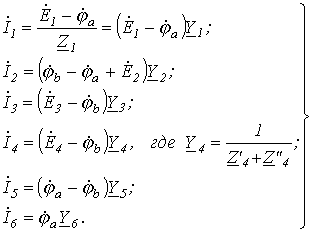
Запишем уравнение по первому закону Кирхгофа для узла а:
и подставим значения входящих в него токов, определенных выше:
.
Сгруппировав соответствующие члены, возьмём:
.
Подобно возможно записать для узла b:
.
Как и по способу контурных токов, совокупность уравнений по способу узловых потенциалов возможно составлена формальным методом. Наряду с этим нужно руководствоваться следующими правилами:
1. В левой части i-гоуравнения записывается со знаком “+”потенциал i-го узла, для которого составляется данное i-е уравнение, умноженный на сумму проводимостей ветвей, присоединенных к данному i-му узлу, и со знаком “-”потенциал соседних узлов, любой из которых умножен на сумму проводимостей ветвей, присоединенных к i-му и k-му узлам.
Из сообщённого направляться, что все члены , стоящие на основной диагонали в левой части совокупности уравнений, записываются со знаком “+”, а все остальные – со знаком “-”, причем . Последнее равенство по аналогии с способом контурных токов снабжает симметрию коэффициентов уравнений довольно основной диагонали.
2. В правой части i-гоуравнения записывается так называемый узловой ток , равный сумме произведений ЭДС ветвей, подходящих к i-му узлу, и проводимостей этих ветвей. Наряду с этим член суммы записывается со знаком “+”, в случае, если соответствующая ЭДС направлена к i-му узлу, в другом случае ставится символ “-”. В случае, если в подходящих к i-му узлу ветвях находятся источники тока, то символы токов источников токов, входящих в узловой ток несложными слагаемыми, определяются подобно.
Подводя итог напомним, что выбор того либо иного из рассмотренных способов определяется тем, что направляться отыскать, и тем, какой из них снабжает меньший порядок совокупности уравнений. При расчете токов при однообразном числе уравнений предпочтительнее применять способ контурных токов, поскольку он не требует дополнительных вычислений с применением закона Ома. Способ узловых потенциалов весьма эргономичен при расчетах многофазных цепей, но не эргономичен при расчете цепей со обоюдной индуктивностью.
Литература
1. Основытеории цепей: Учеб.для институтов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
2. Бессонов Л.А.Теоретические базы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных профессий институтов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с
.
задачи и Контрольные вопросы
1. В ветви на рис. 1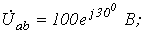 
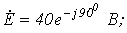
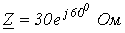. Выяснить ток .
Ответ: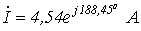 
.
2. В чем содержится сущность символического способа расчета цепей синусоидального тока?
3. В чем состоит сущность способа контурных токов?
4. В чем состоит сущность способа узловых потенциалов?
5. В цепи на рис. 5 ; ;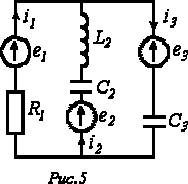 
; . Способом контурных токов выяснить комплексы действующих значений токов ветвей.
Ответ: ; ; .
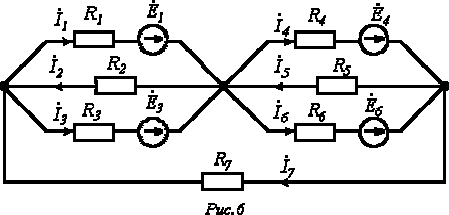
6. В цепи на рис. 6 . Вычислить токи в ветвях, применяя способ узловых потенциалов.
Ответ: ; ; ; ; ; ; .
Рассмотренные способы расчета электрических цепей – конкретно по законам Кирхгофа, способы контурных токов и узловых потенциалов – разрешают принципиально вычислить любую схему. Но их использование без применения введенных ранее топологических матриц рационально для довольно несложных схем. Применение матричных способов расчета разрешает формализовать процесс составления уравнений электромагнитного баланса цепи, и упорядочить ввод данных в ЭВМ, что особенно значительно при расчете сложных разветвленных схем. 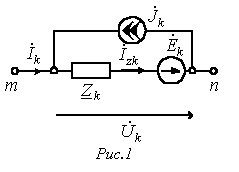 Переходя к матричным способам расчета цепей, запишем закон Ома в матричной форме. Пускай имеем схему по рис. 1, где — источник тока. В соответствии с рассмотренным нами ранее законом Ома для участка цепи с ЭДС для данной схемы возможно записать: |
| . | (1) |
Но, для предстоящих выкладок будет удобнеепредставить ток как сумму токов k-й источника и ветви тока, т.е.:
| . | (2) |
Подставив (2) в (1), возьмём:
| . | (3) |
Формула (3) представляет собой аналитическое выражение закона Ома для участка цепи с источниками ЭДС и тока (обобщенной ветви).
Соотношение (3) запишем для всех n ветвей схемы в виде матричного равенства
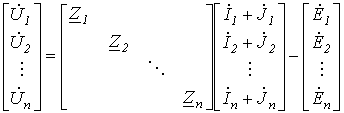
либо
| , | (4) |
где Z – диагональная квадратная (размерностью n x n) матрица сопротивлений ветвей, все элементы которой (обоюдную индуктивность не учитываем), за исключением элементов основной диагонали, равны нулю.
Соотношение (4) представляет собой матричную запись закона Ома.
В случае, если обе части равенства (4) умножить слева на контурную матрицу В и учесть второй закон Кирхгофа, в соответствии с которому
| , | (5) |
то
| , | (6) |
другими словами приобрели новую запись в матричной форме второго закона Кирхгофа.