Уравнения гармонического баланса (6.5) с применением
комплексных коэффициентов усиления линейного и нелинейного звеньев возможно записать следующим образом:
Wн(Xm)Wл(j?)=-1 (6.11)
либо Wл(j?)=-1/Wн(Xm)=Vн(Xm).
Из последнего равенства разумеется, что параметры автоколебаний (частоту ? и амплитуду Хm) возможно обнаружить пересечении годографа линейной динамической части и инверсного годографа нелинейного элемента, забранного со знаком минус (рис.6.2). Как видно из рисунка, два годографа пересекаются в двух точках М и N, определяющих вероятные автоколебания с параметрами соответственно.
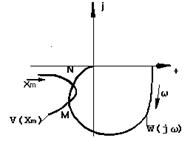 Рис.6.2 |
Не каждое из отысканных ответов соответствует устойчивым автоколебаниям, т.е. таким, каковые по окончании краткосрочного действия на совокупность, восстанавливаются. Для определения устойчивости автоколебаний возможно воспользоваться достаточным критерием Гольдфарба, честным для устойчивой линейной части совокупности, что формулируется следующим образом.
При перемещении по годографу V(Xm) в сторону повышения амплитуды Хm точке пересечения годографов, проходя через которую мы выходим из контура амплитудно-фазовой чёрта линейной части совокупности, соответствует устойчивое автоколебание. Так, параметры автоколебаний в совокупности определяются по пересечению двух годографов в точке М.
Определение параметров автоколебаний по логарифмическим чертям
Для определения параметров автоколебаний нелинейных совокупностей с однозначными нелинейностями комфортно пользоваться логарифмическими амплитудными и фазовыми характеристиками на базе соотношений, взятых из (6.11)
|Wн(Xm)|*|Wл(j?)|=1,
?н(Xm)+?л(?)=-?. (6.12)
Из первого соотношения направляться |Wл(j?)|=|1/Wн(Xm)| либо
с учетом того, что для однозначных нелинейных черт Кс=0
|Wл(j?)|=|1/Ks(Xm)|,либо по окончании логарифмирования правой и левой частей
Lл(?)=-Lн(Xm), (6.13)
где Lл(?)=20lg|Wл(j?)|, -Lн(Xm)=20lg|1/Ks(Xm)|.
Из второго соотношения для однозначных нелинейных
черт, для которых ?н(Xm)=0, направляться ?л(?)=-?. (6.14)
Так, равенства (6.13) и (6.14) определяют условия происхождения автоколебаний и из них смогут быть отысканы параметры вероятных автоколебаний. Но не всякое ответ соответствует устойчивым автоколебаниям. Для определения устойчивости автоколебаний пользуются следующими правилами:
1. в случае, если при повышении ординаты и амплитуды логарифмической характеристики –Lн(Xm) возрастают, то линия “-?” штрихуется сверху, а в противном случае — снизу;
2. в случае, если при повышении частоты ? фазовая черта линейной части ?л(?) пересекает прямую -?, переходя с заштрихованной стороны на незаштрихованную, то автоколебания — устойчивы, а в противном случае — неустойчивы.
Так, для определения параметров автоколебаний в замкнутой совокупности с нелинейным элементом, имеющим однозначную чёрта, на одном графике строятся характеристики Lл(?) и -Lн(Xm)(разумеется, что ? и Хm откладываются на различных участках однойоси абсцисс в логарифмическом масштабе); фиксируется точка ?0, для которой выполняется условие (6.14) и из равенства (6.13) определяется амплитуда Хm0 вероятных автоколебаний; проверяется устойчивость автоколебаний.
На рис.6.3 продемонстрирован пример определения параметров автоколебаний в замкнутой совокупности с нелинейностью типа насыщение, коэффициенты гармонической линеаризации которой приведены в табл. 6.2.
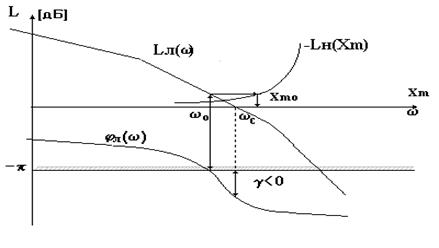
Рис.6.3
В лабораторной работе исследуется независимая нелинейная совокупность (рис.6.1), линейная часть которой задана в лабораторной работе № 2 с нелинейностью, заданной в табл.6.1 с параметрами, соответствующими номеру бригады. Наряду с этим для неоднозначной нелинейной чёрта рекомендуется пользоваться построением годографов, а для однозначной — логарифмических черт линейной и нелинейной частей разомкнутой совокупности.
Подготовка к работе
1. Выстроить амплитудно-фазовую чёрта линейной части совокупности Wл(j?), заданной в лабораторной работе № 2, с параметрами из табл. 2.1, определяемыми в соответствии с номером бригады. (Для однозначных нелинейностей рекомендуется строить чёрта Lл(?)).
2. На том же графике выстроить инверсный годограф нелинейного
статического элемента, заданного в табл. 6.1 с параметрами, заданными
в табл. 6.2 в соответствии с номером бригады. (Для однозначных
нелинейностей – чёрта — Lн(Xm)).
3. Выяснить диапазон трансформации коэффициента усиления
разомкнутой совокупности, при котором в нелинейной замкнутой совокупности
смогут появиться устойчивые автоколебания.
Задание на исполнение работы
1. Смоделировать нелинейную независимую совокупность (рис.6.1) с заданными линейной частью и нелинейностями, заданными в таблице 6.1.
2. Задав на интеграторе начальные условия, замечать и снять процессы на выходе линейного (x(t)=y(t)) и нелинейного (z(t)) звеньев.
3. По снятому процессу x(t) выяснить параметры автоколебаний.
4. Замечать фазовый портрет, подавая на вход X сигнал x(t), а на вход Y — производную этого сигнала по времени (сигнал с выхода интегратора).
5. Выяснить параметры автоколебаний по фазовому портрету.
Сравнить полученные параметры с вычисленными заблаговременно.
Методические указания
Определение параметров автоколебаний по фазовому портрету производится, исходя из следующих мыслей. При x(t)=Хmsin?t dx(t)/dt=Хm?sin?t и фазовый портрет будет воображать собой эллипс, из которого возможно отыскать параметры автоколебаний (см. рис. 6.4).
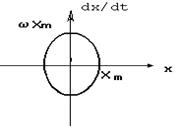
Рис.6.4
Таблица 6.1
| № бригады | |||||||||||||||
| № нелинейности | |||||||||||||||
| № нелинейности |
Параметры нелинейностей: ?=450, b=0.5, b1=0.25, b2=0.5, c=0.75, m=0.5.
Таблица 6.2
| № | Статическая черта нелинейного элемента | Ks(Xm) | Kc(Xm) |
Совершенная релейная 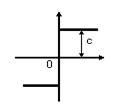
|
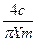
|
||
Релейная с территорией нечувствительности 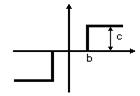
|
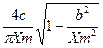
|
||
Релейная с гистерезисной петлей 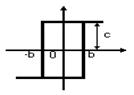
|
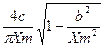
|
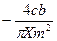
|
|
Релейная с территорией нечувствительности 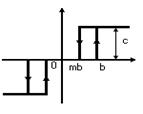
|
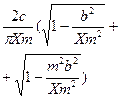 при Xmb |
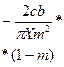
|
|
С насыщением 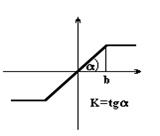
|
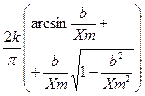 при Xm?b |
С гистерезисной петлёй и насыщением 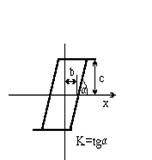
|
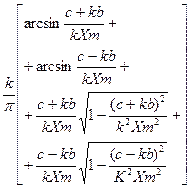 при 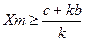
|
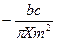
|
Контрольные вопросы
- При каких догадках и как выводятся уравнения гармонического баланса.
- В какой форме и как возможно представить комплексный коэффициент усиления нелинейного звена?
- Выведите выражения, определяющие коэффициенты гармонической линеаризации.
- Что такое автоколебания, как выяснить их параметры, в каком случае имеют место устойчивые автоколебания?
- Выведите выражения коэффициентов гармонической линеаризации для заданных видов нелинейных элементов.
Литература
1. Теория автоматического управления. Ч. II. Под ред. Нетушила А.В., М.: Высш. школа, 1982, 400 c.
ПРИЛОЖЕНИЕ 1
Диалоговое окно Simulation Parameters
1) Вкладка Solver (Решатель ОДУ)
Эта вкладка включает три группы опций. Первая несколько опций Simulation time(Время моделирования) содержит текстовые поля для задания начального (Start time)и конечного (Stop time)времени интегрирования, где по умолчанию устанавливаются значения 0 и-10, соответственно. Несколько опций Solver options(Опции решателя) включает раскрывающийся перечень Туре(Тип) для задания параметров управления шагом интегрирования и раскрывающийся перечень указания имени функции, которая интегрирует совокупность ОДУ. Все функции по большей части разбиваются на две группы: функции, реализующие способы с переменным шагом интегрирования, и применяющие способы с постоянным шагом интегрирования, кое-какие функции относятся к обеим группам. При выбора пункта Variable step,становятся дешёвыми текстовые поля Min step size(Минимальный размер шага интегрирования), Max step size(Большой размер шага интегрирования), текстовое поле Initial step size(Начальный ход интегрирования) и текстовые поля Relative tolerance(Относительная погрешность) и Absolute tolerance(Безотносительная погрешность). При выборе пункта Fixed-step значение шага интегрирования задается в соответствующем текстовом поле. В группе опций Output options(Опции выходной переменной) выбирается метод формирования выходного массива.
Совокупность Simulink разрешает использовать разные численные способы ответа ОДУ, каковые адекватно отображают уровень современной теории численного интегрирования и являются стандартным средством, реализованным в виде действенного ПО. На данный момент чаще всего употребляются функции, основанные на формулах интегрирования с переменным шагом, т. к. в этом случае величина шага интегрирования изменяется от одной расчетной точки к второй, наряду с этим значение локальной погрешности разрешает осуществлять контроль размер следующего шага и не появляется необходимость ограничивать величину шага для получения ровной кривой — траектории выходной переменной.
В таблице 1.1 приведены функции, применяемые для интегрирования, и указано их назначение.
При выбора пункта Variable stepв раскрывающемся перечне Турев группе опций Output optionsна вкладке Solverможно задавать расстояние между точками траектории выходной переменной. Эти опции не употребляются при формул интегрирования с постоянным шагом. Раскрывающийся перечень содержит три пункта: Refine output(Выход с уточнением), Produce additional output(Формирование расширенного выхода), Produce specified output only(Формирование установленного выхода).
При выборе пункта Refine outputмежду моментами времени интегрирования добавляются промежуточные точки, после этого строятся кусочно-интерполирующие многочлены (последовательный сплайн-способ) и с их помощью рассчитываются промежуточные точки ответа, что уменьшает время ответа задачи если сравнивать с подходом, связанным с уменьшением шага интегрирования. Пункт Refine outputвыбирается, в то время, когда нужно представить график трансформации компонентов вектора выхода в зависимости от времени в виде ровных кривых. В случае, если в раскрывающемся перечне выбран пункт Refine output,то делается дешёвым текстовое поле Refine factor(Коэффициент для уточнения). Вводимый параметр — целое число. Совокупность Simulink дробит величину каждого шага на значение коэффициента Refine factor. К примеру, в случае, если значение коэффициента равняется 2, любой ход интегрирования делится пополам, и значения ответа будут добавлены к массиву выходных данных. Пункт Produce additional output(Формирование расширенного выхода) раскрывающегося перечня Output optionпозволяет объединить и указать в строго возрастающем порядке элементы двух массивов — моментов времени фиксированных моментов и интегрирования времени, задаваемых пользователем в текстовом поле Output times(Моменты времени выхода). К примеру, в случае, если нужно добавить вектор, компоненты которого являются моментами времени с промежутком 10 с, и наряду с этим значения начального и конечного времени моделирования равны 0 и 100 соответственно, то в текстовое поле Output какое количество ввести оператор вида [0:10:100].
Выбор пункта Produce specified output only(Формирование установленного выхода) нужен чтобы выходной массив содержал решения в установленные моменты времени. К примеру, возможно выбрать этот пункт , если нужно сравнить пара выходных массивов для оценки влияния трансформации параметров блоков структурных схем.
Таблица 1.1
| Функция Назначение ode45 Действенный одношаговый решатель неспециализированного назначения. Реализуются явные способы Рунге-Кутты четвертого и пятого порядков точности. Функция ode45 выбирается совокупностью по умолчанию и рекомендуется для интегрирования новой совокупности ОДУ; ode23 Употребляются способы Рунге-Кутты второго и третьего порядков. Рекомендуется для ответа умеренно твёрдых задач. Функция требует меньшего размера шага интегрирования, чем функция ode45 для обеспечения сравнимой точности; odel 13 Реализуется способ Адамса-Башворта-Мултона переменного порядка. Функция odell3 применяет многошаговые разностные способы, исходя из этого обеспечиваются такие же требования к точности, как для функций ode45 либо ode23 при меньшем количестве вычислений производных в промежуточных точках, что снабжает более высокую скорость интегрирования. Функция не предназначена для интегрирования совокупностей дифференциальных уравнений, правые части которых имеют разрыв. Описание функции odel 13 приводится в литературе по численным способам [2]; ode 15s Употребляется формула неявного многошагового разностного способа (формула дифференцирования назад) с переменным порядком точности схемы для твёрдых задач. В случае, если использование функции ode45 дает низкую скорость интегрирования, рекомендуется обращаться к функции ode 15s; ode23s Реализуется модифицированный способ Розенброка с постоянным шагом и фиксированным порядком точности. Функция предназначена для интегрирования умеренно твёрдых задач с низкими требованиями по точности. Данный одношаговый решатель обычно имеет громадную скорость интегрирования, чем функция ode 15s. При твёрдых задач рекомендуется выбрать действенный решатель методом сравнений; ode23t Реализуется одношаговая разностная схема предиктор-корректор (способ трапеций). Рекомендуется для умеренно твёрдых задач. Функции ode23t и ode23tb имеют схожие методы, используемые в решателе. Функция ode23t снабжает более высокую скорость интегрирования; ode23tb Употребляется способ трапеций (подобно функции ode23t) на первой стадии, на втором — формула обратного дифференцирования. Имеет низкий порядок точности и меньшую скорость интегрирования, чем функция ode23t; discrete Реализуется аналитический способ нахождения ответа разностных уравнений с заданным шагом дискретности; ode5 Употребляется явный способ Рунге-Кутты пятого порядка точности с фиксированным шагом интегрирования. Этот метод употребляется в функции ode45; ode4 Реализуется хороший явный способ Рунге-Кутты четвертого порядка точности с фиксированным шагом интегрирования; ode3 Употребляется явный способ Рунге-Кутты третьего порядка точности с фиксированным шагом. Метод употребляется в функции ode 23; ode2 Употребляется явный способ Рунге-Кутты второго порядка точности с фиксированным шагом; odel Употребляется явный способ Эйлера с фиксированным размером шага. |
При выборе пункта Produce specified output onlyв текстовом поле Output times вводится вектор, компоненты которого соответствуют требуемым моментам времени.
2) Вкладка Workspace I/O (экспорт и Импорт данных рабочей области)
Вкладка Workspace I/O(экспорт и Импорт данных рабочей области) продемонстрирована на рис. 1.11. С ее помощью возможно загружать эти из рабочей области совокупности MATLAB и размещать выходные массивы в рабочей области. Вкладка содержит три группы опций: Load from workspace(Загрузка из рабочей области), Save to workspace(Размещение в рабочей области) и Save options(Сохранение значений опций).
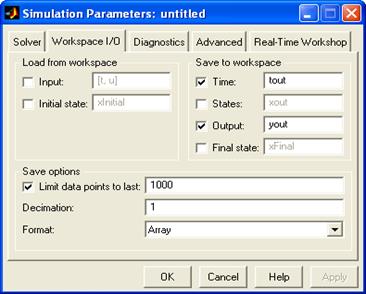
Рис. 1.11. Вкладка Workspace I/O
Математическая модель совокупности Simulink имеет форму совокупности нелинейных дифференциальных либо разностных уравнений первого порядка, представленной в явной форме. В совокупности Simulink вектор переменных состояния включает компоненты, определяемые переменными состояния блоков интеграторов, компоненты, неявно задаваемые переменными состояния блоков передаточных функций, блоков моделей в пространстве состояний, блоков нелинейностей, блоков других типов и дискретных систем блоков.
Совокупность Simulink снабжает возможность доступа к вектору переменных состояния модели, с применением вкладки Workspace I/O.
Для загрузки массива данных, включающего вектор, компоненты которого являются моментами времени, в группе опций Load from workspaceустанавливается флажок Input(Входные эти). Операция загрузки выполняется совместно с блоком In из библиотеки блоков Sources. Блок In (Входной порт) конфигурируется для скалярных и векторных переменных. В текстовом поле Inputзадается оператор, включающий имена переменных, которым присваиваются значения массива моментов времени (по умолчанию задается имя переменной t) и массива (по умолчанию имя переменной и), включающего столбцы, любой из которых соответствует компоненту вектора входной переменной (любая строчок массива соответствует моменту времени). В случае, если заданы более чем один блок In, номера столбцов входного массива устанавливаются в соответствии с числом — индикатором, определенным для блоков In. Первый столбец в массиве соответствует блоку с мельчайшим номером, последний столбец — блоку In с наивысшим номером. В случае, если блок In имеет вектор входной переменной, то для каждого компонента вектора задается вектор-столбец в массиве и.
Для загрузки начальных состояний, соответствующих внутренним переменным состояния из рабочей области совокупности MATLAB, на вкладке Workspace I/Oследует установить флажок Initial state(Начальное состояние).
Все вектора переменных состояния совокупности Simulink имеют заданные по умолчанию начальные значения (как правило устанавливается 0). Начальные условия для блоков Integrator смогут быть заданы в диалоговом окне блока. Редактирование начальных условий, заданных по умолчанию, включая значения, установленные в диалоговом окне блока Integrator, осуществляется на вкладке Workspace I/O.В текстовом поле Initial stateзадается имя переменной, которой присваивается значение вектора начальных состояний модели (по умолчанию имя переменной xI-nitial), которая размещается в рабочей области совокупности MATLAB перед запуском процесса моделирования. Вектор начальных состояний должен иметь размерность, равную размерности вектора переменных состояния модели, это возможно вектор-столбец либо вектор-строчок.
В текстовом поле Time(Моменты времени) задается имя переменной, которой присваивается значение указанного массива (по умолчанию имя переменной tout).
В текстовом поле States(Состояния) задается имя переменной, которой присваивается значение массива в рабочей области совокупности MATLAB (по умолчанию имя переменной xout). Операция размещения массива в рабочей области выполняется совместно с блоком Out (Выходной порт) и подобна рассмотренному ранее сотрудничеству с блоком In. В текстовом поле Final state(Конечное состояние) задается имя переменной, которой присваивается значение вектора переменных состояния для момента времени окончания моделирования (по умолчанию имя переменной xFi-nal), размещенного в рабочей области. Этот вектор возможно применять для задания начальных состояний (текстовое поле Initial state)для исполнения процесса моделирования, начальное время которого равняется конечному времени прошлого процесса.
Несколько опций Save optionsвкладки Workspace I/Oсвязана с хранением переменных в рабочей области. В текстовом поле Limit data points to lastустанавливается предельное число элементов массива, размещаемого в рабочей области совокупности MATLAB. К примеру, в случае, если установлен флажок Limit data points to lastи в соответствующем текстовом поле вводится значение 1000, это указывает, что последние 1000 точек массива сохраняются в рабочей области. В текстовом поле Decimation(Коэффициент выборки) задается целое число — коэффициент выборки для массива, создаваемого в рабочей области: в случае, если значение равняется 2, тогда лишь каждая вторая строчок массива размещается в рабочей области, в случае, если задано 1, то сохраняются все точки массива. В раскрывающемся перечне Formatвыбирается пункт, соответствующий типу данных: тип данных числовой массив Array(устанавливается по умолчанию) либо тип данных массив записей, в котором в одном случае полю моментов времени присваивается некое значение (StructureWithTime),а в другом случае присваивается безлюдной массив (Structure).
3) Вкладка Diagnostics (Диагностика)
На вкладке Diagnostics(рис. 1.12) определяются действия при происхождения заданных обстановок, устанавливаются опции для автоматической проверки непротиворечивости параметров выходных переменных блоков и контроля предельных значений. На данной вкладке в группе опций Actionимеются три тумблера. В случае, если устанавливается тумблер None(Нет), то совокупность Simulink игнорирует указанную обстановку. При установке тумблера Warning(Предупреждение) либо Error(Неточность) при происхождения данных обстановок выводится предупреждение либо прерывается процесс моделирования и выдается сообщение об неточности, соответственно.
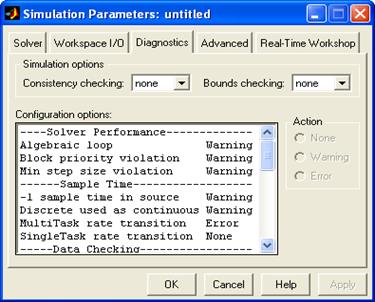
Рис. 1.12. Вкладка Diagnostics
Алгебраические контуры являются свойством модели, которое показывает, что в каком-либо канале между выходами модели и входами отсутствуют динамические звенья. Контуры без динамических звеньев существенно снижают скорость интегрирования, а во многих случаях процесс моделирования прерывается. Для пункта Algebraic loopрекомендуется установить тумблер Warning.В случае, если в модели допускается применение алгебраических контуров, то направляться установить тумблер в положение None.
Обстановка Min step size violation(Нарушение условия на минимальный размер шага) появляется, в то время, когда функция интегрирования вынуждена применять размер шага, значение которого меньше, чем фиксированная величина, заданная на вкладке Solverв текстовом поле Min step size,что для формул с переменным шагом интегрирования не допускается. При происхождении данной обстановке используются формулы интегрирования меньшего порядка точности. Также, возможно расширить значения допустимых относительной и безотносительной погрешностей, задаваемых на вкладке Solver.Для ситуации Min step size violationнеобходимо установить тумблер Warningили Error,так как данное событие говорит о том, что численное интегрирование выполняется лишь при низких требованиях к точности.
Обстановка Unconnected block input(Несоединенный входной порт блока) появляется, в то время, когда блок имеет входной порт, что не употребляется. Обычно это происходит в следствии некорректно выстроенной модели. В этом случае направляться установить тумблер Errorили Warning.В случае, если эта неточность задания входного порта блока есть преднамеренной, тогда выходной порт блока Ground (заземление) из библиотеки блоков Sources (Источники сигналов) соединяется с упомянутым входным портом.
Обстановка Unconnected block output(Несоединенный выходной порт блока) появляется, в то время, когда блок имеет выходные порты, не соединенные с входными портами вторых блоков. Методом ее разрешения есть соединение неиспользованных выходных портов блока с входным портом блоков Terminator (Оконечная нагрузка) из библиотеки блоков Sinks (Средства регистрации). Эта обстановка требует установки тумблера Warningили Error.
Обстановка Unconnected line(Несоединенная линия связи) практически в любое время обусловлена неточностью в построении модели совокупности Simulink и появляется, в случае, если конечная точка линии связи не связана с входным портом блока. В этом случае устанавливается тумблер Error.
Обстановка -1 sample time in source(В источнике период квантования -1) появляется, в то время, когда для периода квантования блока источника сигнала задается значение, равное -1. Это говорит о том, что блок источника сигнала обязан считывать значение периода квантования из блока, с которым он соединен. Это не есть неточностью, но, для блоков источников сигналов целесообразно задавать данную величину в явном виде. Эта обстановка на первой стадии обязана обрабатываться с установленным тумблером Warning,после этого при задании в соответствующих блоках значений периода квантования тумблер устанавливается в None.
Обстановка Unneeded type conversion(He требуемый тип преобразования) появляется, в то время, когда происходит переопределение типа переменной, которое не есть нужным, и, наряду с этим, данное преобразование не есть некорректным. В этом случае устанавливается тумблер None.
Обстановка int 32 to float conversion(Преобразование типа целое с 32 битами на элемент в форму числа с плавающей точкой) может привести к накоплению погрешностей округления и повлиять на результирующую погрешность. Для данного пункта устанавливается тумблер Warningили Error.
Обстановка Data overflow(Переполнение разрядной сетки) видится, в то время, когда величина амплитуды сигнала либо значение элемента внутреннего массива превышает предельное значение, заданное для их типа данных. Переполнение разрядной сетки в любых ситуациях есть важной неточностью, исходя из этого эта обстановка обрабатывается при установке тумблера Errorили Warning.
В группе опций Simulation options(Опции моделирования) в раскрывающемся перечне Consistency checking(Проверка на непротиворечивость) выбирается значение, разрешающее делать действия при происхождении неточностей в блоках пользователя. Проверка на непротиворечивость не есть необходимой при применении стандартных блоков совокупности Simulink, но эти обстановки уменьшают скорость интегрирования. В большинстве случаев, для опции Consistency checkingзадается значение None.
4) Вкладка Advanced (Экспертные настройки)
Вкладка Advanced(Экспертные настройки) (рис. 1.13) разрешает задавать последовательность опций для управления скоростью интегрирования, размером памяти, выделяемой под процесс, фиксацией события пересечения нулевого значения и ослаблением правил для переменных булевского типа, контролируемых в ряде блоков. Для этих опций устанавливаются значения on либо off. Модели последовательности блоков совокупности Simulink описываются функциями, имеющими разрывы. К примеру, выходная переменная блока Sign (Символ) из библиотеки блоков Nonlinear (Нелинейности) имеет значение, равное 1, в случае, если входная переменная имеет хорошее значение, 0, в случае, если вход равен 0, либо -1, в случае, если входной сигнал есть отрицательным. Эта функция имеет разрыв в точке нуль. При применении функции интегрирования, реализующей формулу с переменным шагом интегрирования, значение шага будет пересчитываться, в то время, когда входная переменная блока Sign примерно равна 0. Данное явление связано с фиксацией события пересечения нулевого значения. Обнаружение данных событий оказывает помощь повысить точность процесса моделирования, но, во многих случаях происходит понижение скорости интегрирования, отмечается процесс колебаний с громадной частотой около точки разрыва (данное явление именуется «дребезг») и процесс интегрирования может фактически остановиться, т. к. размер шага значительно уменьшается до малого значения.
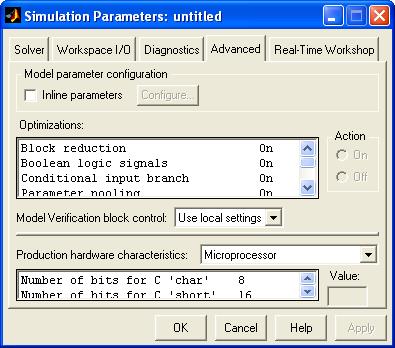
Рис. 1.13. Вкладка Advanced
В случае, если модель включает пара блоков, для которых фиксируются события пересечения нулевого значения, то для повышения скорости интегрирования для опции Zero crossing detection(Обнаружение пересечения нулевого значения) устанавливается значение on. направляться иметь в виду, что наряду с этим может возрасти погрешность расчета вектора ответа. Этот подход употребляется при происхождении явления «дребезг». В случае, если задание значения on для опции Zero crossing detectionзначительно повышает скорость интегрирования, то направляться распознать и, по возможности, устранить обстоятельство происхождения указанного явления.
Для управления памятью в совокупности Simulink употребляются буферы памяти, каковые поддерживают не все линии связи. Блоки Floating Scope (Плавающий осциллограф) используются для визуализации переменных, что требует выделения памяти для линий связи, и исходя из этого для опции Signal storage reuse(Многократное применение памяти для сигнала) задается значение off. Эти операции выполняются на этапе ее отладки и построения модели, т. к. по окончании запуска моделирования будет наблюдаться ухудшение показателей использования процесса памяти и эффективности моделирования.
Последовательность блоков совокупности Simulink, таких как блоки логики, имеют на входе массивы переменных, обрисовываемых булевским типом данных, каковые будут выдавать сообщение об неточности, в случае, если тип данных входной переменной не есть булевским. Для подавления сообщения об неточности для опции Boolean logic signalsуказывается значение off. Это снабжает совместимость с более ранними предположениями совокупности Simulink, в которых употреблялись числовые массивы удвоенной точности в форме с плавающей точкой. При установке значения off для опции Boolean logic signalsблоки логики будут допускать переменные в форме с плавающей точкой. В этом случае значению 0.0 соответствует булево значение False, а любому второму значению — булево значение True.
СОДЕРЖАНИЕ
| Лабораторная работа № 1. Изучение программного комплекса по исследованию и моделированию динамических совокупностей “Simulink”. Изучение типовых динамических звеньев . . . . . . . . . . . . . . . . . . . . | ||
| Лабораторная работа № 2. Изучение качества совокупностей автоматического управления . . . . . . . . . . . . . . . . | ||
| Лабораторная работа № 3. Коррекция совокупностей автоматического управления . . . . . . . . . . . . . . . . . . . . . . . | ||
| Лабораторная работа № 4.Изучение линейных импульсных автоматических совокупностей . . . . . . . . . . . . . . . | ||
| Лабораторная работа № 5. Изучение релейных совокупностей автоматического регулирования способом фазовой плоскости . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | ||
| Лабораторная работа № 6. Изучение нелинейных совокупностей автоматического управления способом гармонического баланса . . . . . . . . . . . . . . . . . . . . . . . . . . . | ||
| ПРИЛОЖЕНИЕ 1.Диалоговое окно Simulation Parameters |
Учебное издание
Т.В. Ягодкина, С.А. Хризолитова, В.М. Беседин,
О.А. Бондин, Е.Н. Грачев
ИЗУЧЕНИЕ САУ С ПРИМЕНЕНИЕМ
ПРИКЛАДНОГО ПАКЕТА MATLAB
Лабораторный практикум
по курсу
«Базы автоматического управления»
Редактор М.Б. Коломейцева
Технический редактор Е.Н. Касьянова
Темплан издания МЭИ 2006 (II), способ.
Подписано к печати 11.02.2006г.
Формат бумаги 60х84/16
Физ. печ. л. 3,25 Тираж 50 Изд.N242заказ
Издательство МЭИ, 111250, Москва, Красноказарменная, д.14
Типография Издательства МЭИ, Красноказарменная, 13