ВЫБОР МЕСТА Размещения ПИТАЮЩИХ ПОДСТАНЦИЙ ПРОМЫШЛЕННОГО ПРЕДПРИЯТИЯ
НЕСПЕЦИАЛИЗИРОВАННЫЕ ПОЛОЖЕНИЯ О ВЫБОРЕ Расположения ПИТАЮЩИХ ПОДСТАНЦИЙ
Подстанция (основная понизительная ГПП, основная распределительная ГРП, цеховая трансформаторная ТП) есть одним из главных звеньев электрической системы любого промышленного предприятия. Исходя из этого оптимальное размещение подстанций на территории промышленного предприятия — наиболее значимый вопрос при построении рациональных систем электропитания. При проектировании электрических систем фирм разных индустрии разрабатывается генплан проектируемого объекта, на что наносятся все производственные цехи. Размещение цехов определяется технологическим процессом производства.
На главном замысле указываются установленные либо расчетные мощности всего предприятия. Помимо этого, в проекте имеются графики электрических нагрузок вышеуказанных цехов и всего предприятия. Одной из главных задач проектирования есть оптимальное размещение ГПП, ГРП и ТП на территории промышленного предприятия. Это указывает, что размещение всех подстанций должно соответствовать самоё рациональному сочетанию капитальных затрат на сооружение эксплуатационных расходов и системы электроснабжения.
Для определения расположения ГПП, ГРП и ТП при проектировании электрической системы на генплан промышленного предприятия наносится картограмма нагрузок.
КАРТОГРАММА НАГРУЗОК
Картограмма нагрузок предприятия представляет собой размещенные по генплану окружности, причем площади, ограниченные этими окружностями, в выбранном масштабе равны расчетным нагрузкам цехов. Для каждого цеха наносится собственная окружность, центр которой сходится с центром нагрузок цеха. Центр нагрузок цеха либо предприятия есть символическим центром потребления электроэнергии цеха (предприятия). Основную понизительную, распределительную и цеховые подстанции направляться располагать как возможно ближе к центру нагрузок. Это разрешает приблизить высокое напряжение к центру потребления электроэнергии и существенно сократить протяженность, как распределительных сетей большого напряжения предприятия, так и цеховых электрических сетей низкого напряжения, уменьшить расход проводникового материала и снизить утраты электроэнергии.
Картограмма электрических нагрузок разрешает проектировщику достаточно наглядно представить распределение нагрузок на территории промышленного предприятия. Как уже отмечалось, картограмма нагрузок предприятия складывается из окружностей и площадь, ограниченная каждой из этих окружностей в выбранном масштабе т равна расчетной нагрузке соответствующего цеха Pi :
Pi =
Из этого выражения радиус окружности
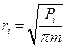
где т — масштаб для определения площади круга.
Любой круг возможно разделен на секторы, соответствующие осветительной и силовой нагрузкам. В этом случае картограмма дает представление не только о значении нагрузок, но и об их структуре. Но картограммы направляться наносить на генплан промышленного предприятия раздельно для активной и реактивной нагрузок. Обстоятельством этого есть то событие, что питание активных и реактивных нагрузок производится от различных источников.
Питание активных нагрузок обеспечиваемся либо от собственных электростанций промышленного предприятия, либо от подстанций энергосистемы. Питание реактивных нагрузок осуществляется от конденсаторных батарей, располагаемых в местах потребления реактивной мощности (индуктивного характера), от перевозбужденных синхронных двигателей либо синхронных компенсаторов, каковые, в большинстве случаев, находятся вблизи мест потребления реактивной мощности. В этом случае направляться обнаружить центр либо центры потребления реактивной мощности. Неверный выбор места установки синхронных компенсаторов приводит к перемещению потоков реактивной мощности по элементам электрической системы промышленного предприятия и приводит к значительным потерям электричества. На основании изложенного рекомендуется иметь два генерального плана: один с картограммой активных и второй с картограммой реактивных нагрузок.
Первый вариант нужен для выбора рационального места размещения питающей подстанции ГПП (ГРП), второй оказывает помощь выяснить рациональное размещение компенсирующих устройств (синхронных компенсаторов) в конкретной системе электропитания промышленного предприятия.
ОПРЕДЕЛЕНИЕ УСЛОВНОГО ЦЕНТРА ЭЛЕКТРИЧЕСКИХ НАГРУЗОК
На данный момент имеется последовательность математических способов, разрешающих аналитическим методом выяснить центр электрических нагрузок (ЦЭН) как отдельных цехов, так и всего промышленного предприятия.
Первый способ, применяющий кое-какие положения теоретической механики, разрешает выяснить ЦЭН цеха (предприятия) с большей либо меньшей точностью (приближенно) в зависимости от конкретных требований.
Так, в случае, если вычислять нагрузки цеха равномерно распределенными по площади цеха, то центр нагрузок возможно принять совпадающим с центром тяжести фигуры, изображающей цех в плане.
В случае, если учитывать настоящее распределение нагрузок в цехе, то центр нагрузок уже не будет совпадать с центром тяжести фигуры цеха в плане, и нахождение центра нагрузок сведется к определению центра тяжести данной совокупности весов.
Наличие многоэтажных строений цехов обусловливает учет в расчетах третьей координаты z.
Совершив аналогию между электрическими нагрузками и массами цехов Pi координаты их центра возможно выяснить в соответствии со следующими формулами:
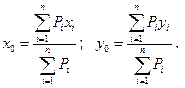
Как продемонстрировала практика проектирования электрических систем предприятий, учета третьей координаты z, в большинстве случаев, не нужно.
Определение центра нагрузок предприятия производится подобно. Данный способ отличается простотой, наглядностью, легко реализуется на ЭВМ (при большом числе цехов), но снабжаемая им точность находится в пределах 5—10%.
Второй способ являющийся разновидностью первого, учитывает не только электрические нагрузки потребителей электричества, но и длительность Тi работы этих потребителей в течение расчетного периода времени. Формулы для определения ЦЭН по этому способу записываются следующим образом:
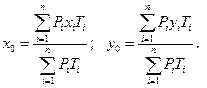
Третий способ, в соответствии с которому рациональное размещение ГПП, ГРП либо ТП должно соответствовать минимуму приведенных годовых затрат, предусматривает для определения электрических нагрузок ответ совокупности алгебраических уравнений способом несложной итерации.
Сейчас при ответе задач построения рациональных электрических систем взяли распространение новые математические способы оптимизации — планирование экстремальных опытов (способ крутого восхождения, градиентный, случайного поиска, симплексный и т п ), каковые разрешают решать различные задачи проектирования, которые связаны с нахождением оптимальных значений разных параметров Так, к примеру, посредством симплексного способа возможно выяснить ЦЭН, выстроить модель разглядываемой совокупности с учетом всех значительных факторов, воздействующих на выбор координат центра нагрузок. Данный способ несложнее по собственной структуре, чем итеративный (с учетом всех ограничений и дополнительных условий).
направляться учесть, что во всех обрисованных выше способах определения ЦЭН линия (кабельная либо воздушная), связывающая потребителей электричества с подстанцией (ГПП, ГРП и ТП), координаты которой мы находим, принимается прямолинейной.
В конечном итоге, в случае, если схема электроснабжения задана, то в зависимости от характера технологического топографического размещения и процесса производства цехов на генплане предприятия конфигурация распределительной сети промышленного предприятия будет такова, что линии в большей либо меньшей степени будут отклоняться от прямолинейных. Исходя из этого по окончании определения теоретического ЦЭН в формулы для нахождения ЦЭН направляться подставить настоящие длины линий.
Все узнаваемые способы нахождения ЦЭН сводятся к тому, что центр электрических нагрузок определяется как некая постоянная точка на генплане промышленного предприятия. Как продемонстрировали изучения, такое положение нельзя считать верным и отысканный выше ЦЭН направляться разглядывать как некий условный центр, поскольку определение его еще не решает до конца задачи выбора расположения подстанций. Дело в том, что положение отысканного по тому либо иному математическому способу условного центра электрических нагрузок не будет постоянным.
Это разъясняется следующими обстоятельствами, вызывающими постоянное смещение ЦЭН:
1) трансформациями потребляемой отдельным приемником, цехом, предприятием мощности в соответствии с графиком нагрузок (график претерпевает постоянные трансформации в связи с трансформациями технологического процесса производства, внедрением новых прогрессивных производственных процессов, трансформациями удельного электропотребления на единицу продукции, увеличением применения оборудования за счет интенсификации и автоматизации производственных процессов и т. д.);
2) трансформациями сменности промышленного предприятия;
3) развитием предприятия.
В соответствии со вышесказанным ЦЭН обрисовывает на генплане промышленного предприятия фигуру сложной формы. Исходя из этого вернее сказать не о ЦЭН цеха (предприятия) как некоей стабильной точке на главном замысле, а о территории рассеяния ЦЭН.
Для построения территории рассеяния ЦЭН в зависимости от требуемой точности расчетов употребляется та либо другая формула определения условного центра электрических нагрузок. направляться подчернуть, что задачи, которые связаны с построением рациональных систем электропитания предприятий, относятся к числу оптимизационных, каковые решаются посредством многих математических способов (линейного, динамического программирования, планирования опыта и т. д.).
Возможно разглядеть два подхода к ответу оптимизационных задач в промышленной энергетике: статический и динамический. При статическом подходе к ответу технико-экономических задач проектирования не учитывается изменение электрических нагрузок, что может привести время от времени к принятию неоптимальных вариантов проектируемой сети. При динамическом подходе приобретаемые ответы являются более обоснованными, поскольку наряду с этим учитывается, динамика электрических систем на достаточно долгий период времени (15— 20 лет) и трансформации ее параметров.
Как продемонстрировала практика проектирования и эксплуатации электрических систем объектов разных индустрии, процесс проектирования нужно вести с учетом динамики электрических нагрузок, как отдельных цехов, так и предприятия в целом. Исходя из изложенного выше, возможно заявить, что выбор оптимальных параметров электрической системы, таких как напряжение, сечение, местоположение и число подстанций и т. п. направляться разглядывать как задачи динамического проектирования.
ОПРЕДЕЛЕНИЕ ТЕРРИТОРИИ РАССЕЯНИЯ ЦЕНТРА ЭЛЕКТРИЧЕСКИХ НАГРУЗОК
Для определения территории рассеяния ЦЭН нужно в первую очередь отыскать закон распределения координат ЦЭН. Изучения продемонстрировали, что распределение случайных координат ЦЭН направляться обычному закону распределения (закону Гаусса—Лапласа), т. е.
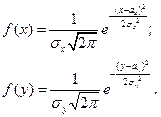
где ax , ay — математические ожидания случайных координат; — дисперсия случайных координат, либо
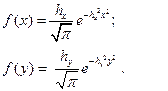
где hx , hy — меры точности случайных размеров:
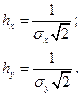
Плотности распределения возможностей случайных координат изображаются в прямоугольной совокупности координат в виде кривой обычного распределения.
Двумерная плотность распределения возможностей случайных свободных координат выражается формулой:
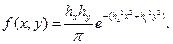
Это выражение получено при условии, что начало координат совмещено с математическим ожиданием. Функция f (x, у) возможно изображена в совокупности хуz поверхностью, носящей наименование поверхности обычного распределения.
| Как видно из приведенных выше выражений, обычный закон распределения определяется при свободных координат четырьмя параметрами: математическими ожиданиями ах и ау, определяющими положение условного ЦЭН, и среднеквадратичными отклонениями ?x, ?y либо мерами точности hx, hy.
В большинстве случаев при определении теоретического закона распределения эти величины малоизвестны и предполагается, что они совпадают с соответствующими размерами эмпирического распределения. Для определения эмпирического закона распределения случайных координат расположим статистическую совокупность случайных координат х в порядке возрастания:
х1, х2, х3, …, хп.
Полное количество вычислений, измерений, наблюдений, дающее каждое из вероятных значений х, именуется частостью появления данного значения
m1, т2, т3, …, тп,
причем разумеется, что
где т — неспециализированное число вычислений, измерений, наблюдений.
Эмпирическая возможность либо эмпирическая частость определяет в относительных единицах долю каждого значения во всей совокупности:
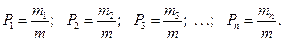
Количество значений, приходящееся на единицу ширины промежутка, именуется эмпирической плотностью распределения:
M1 = 0,
M2 = m1,
M3 = m1 + m2,
. . . . . . . . . . . . .
Mn = m1 + m2 + m3 + . . . + mn-1.
Относительная плотность распределения Fк,э, определяемая как отношение эмпирической плотности распределения к частоте появления данного значения, равна:
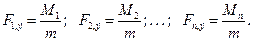
Это выражение определяет эмпирический закон распределения координаты х центра электрических нагрузок, записанный посредством вариационного последовательности. Время от времени эмпирический закон распределения эргономичнее записать посредством таблицы. Подобно возможно отыскан эмпирический закон распределения случайной координаты у. Числовые характеристики отысканного эмпирического распределения определяются из следующих выражений:
 |
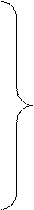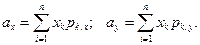
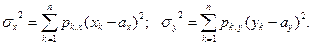(1)
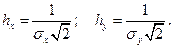
По окончании нахождения закона распределения случайных координат ЦЭН и его числовых черт определим территорию рассеяния ЦЭН. Для этого пересечем поверхность обычного распределения горизонтальной плоскостью H, параллельной плоскости х0у. Проекция взятого сечения на плоскость х0у ограничена кривой, которая описывается выражением
либо
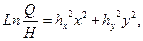(2)
где
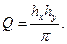
Уравнение (2) является уравнением эллипса, полуоси которого равны:
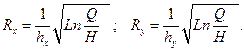
Определим возможность попадания случайных координат вовнутрь ?-эллипса. Обозначив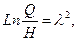 
возьмём уравнение эллипса, что назовем ?-эллипсом
Возможность Р (? ) попадания случайных координат х, у вовнутрь ?-эллипса равна:
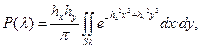
где S? — площадь, ограниченная ?-эллипсом;
Из последнего соотношения видно, что возможность попадания случайной точки х, у в ?-эллипс имеется возрастающая функция параметра ?. Доверительной возможностью того, что случайная точка (х, у) попадает в этот ?-эллипс, именуется такое значение данной возможности, которое считается достаточно родным к единице. Близость доверительной возможности к единице свидетельствует, что попадание случайной точки (х, у) в ?-эллипс фактически точно.
Приняв в качестве доверительной возможности значение Р (?) = = 0,95 и решив последнее уравнение, возьмём, что ?2 = 3.
Следовательно,
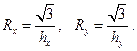
Исходя из изложенного, возможно сделать следующие выводы.
Территория рассеяния центра электрических нагрузок промышленного предприятия является эллипсом . Форма эллипса зависит от соотношения параметров hx и hy. При hx= hy эллипс преобразовывается в круг. Для построения территории рассеяния ЦЭН промышленного объекта достаточно осуществить параллельный перенос осей координат, так дабы начало новой совокупности совпало с математическими ожиданиями ах и ау. Из последнего выражения определяются значения полуосей эллипса, совпадающих по направлению с осями новой совокупности координат, и строится территория рассеяния координат ЦЭН. Расположение основной понизительной либо основной распределительной подстанции на главном замысле выбирается в любой, самая удобной точке выстроенной территории рассеяния ЦЭН. При проектировании электрических систем, у которых наровне с большой сосредоточенной нагрузкой имеется нагрузка, распределенная по всей территории предприятия, территории рассеяния ЦЭН cледует определять раздельно для сосредоточенной и распределенной нагрузок.
По окончании определения территорий рассеяния ЦЭН для сосредоточенных и распределенных потребителей находится неспециализированная территория рассеяния ЦЭН, в случае, если такое объединение целесообразно по технико-экономическим расчетам.
Помимо этого, электрические нагрузки смогут быть размещены по территории промышленного предприятия неравномерно, к примеру сосредоточены в двух либо более местах. В этих обстоятельствах территории рассеяния ЦЭН направляться определять раздельно, разбив на генплане территорию предприятия на части с отдельными сосредоточенными нагрузками. На таких фирмах для построения рациональной системы электропитания значительно чаще сооружаются не одна ГПП либо ГРП, а две либо пара в зависимости от распределения нагрузок и генплана предприятия по его территории. Данный вопрос решается на основании технико-экономических расчетов.
При построении территории рассеяния ЦЭН промышленного предприятия направляться учитывать, что ЦЭН цеха представляет собой также эллипс рассеяния, создаваемый отдельными приемниками либо группами приемников. Из этого следует, что ЦЭН цеха отправляет собственные возмущения не из одной точки (условий ЦЭН), а из различных точек так, как словно бы ЦЭН цеха скользит по собственному эллипсу рассеяния. Поэтому территория рассеяния ЦЭН предприятия, во-первых, возрастает в размерах и, во-вторых, с учетом поворота осей эллипсов рассеяния цехов приближается к окружности.
ОПРЕДЕЛЕНИЕ ОРИЕНТАЦИИ КООРДИНАТНЫХ ОСЕЙ, ОСЕЙ ЭЛЛИПСА РАССЕЯНИЯ И ПОСТРОЕНИЕ ЭЛЛИПСА
Выше было продемонстрировано, что координаты ЦЭН Хо, Yo возможно в силу последовательности обстоятельств разглядывать как случайные размеры, подчиняющиеся обычному закону распределения, причем было принято допущение о независимости этих координат. Поэтому оси эллипса рассеяния строились параллельно осям координат. В общем случае координаты ЦЭН направляться разглядывать как зависимые размеры.
Как мы знаем, что для связанных случайных размеров характерна вероятностная зависимость, которая возможно более либо менее тесной. Эта зависимость определяется коэффициентом корреляции, причем последний характеризует степень тесноты линейной вероятностной связи. В теории возможностей доказывается, что две свободные случайные размеры постоянно являются некоррелированными, но из некоррелированности случайных размеров не всегда следует их независимость.
В случае, если известен последовательность значений пары чисел (Хi, Yi), то эмпирический, т. е. полученный на основании экспериментальных данных, коэффициент корреляции возможно выяснить по следующей формуле:
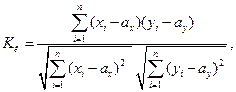
где п — количество пар чисел статистической совокупности (xi, уi); аx- ау — эмпирические математические ожидания, определяемые из выражения (1).
В общем случае коэффициент корреляции может иметь значения в пределах
-1
Исходя из этих мыслей, возможно заявить, что оси эллипса рассеяния образуют с осями координат некий угол а, что определяется следующим образом:
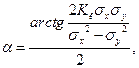
где эмпирические дисперсии, определяемые из выражения (1).
Следовательно, для ориентации осей эллипса рассеяния нужно отыскать угол ?, что составляют оси эллипса рассеяния с осью абсцисс произвольно забранной совокупности координат. Угол ? возможно хорошим либо отрицательным в зависимости от выбранного положения осей координат, величина его находится в прямой зависимости от коэффициента корреляции.
Коэффициент корреляции не изменяется при трансформациях масштаба измерения и начала отсчёта случайных размеров. В большинстве случаев при выборе координатных осей стараются заблаговременно сориентировать координатные оси так, дабы они приблизительно совпали с осями симметрии эллипса рассеяния. В тех случаях, в то время, когда это сделать заблаговременно нереально, для построения эллипса рассеяния начало координат нужно перенести в точку ах, ay, а координатные оси развернуть на угол ?, определяемый последним выражением. Наряду с этим обычный закон распределения в новой совокупности координат ?, ? будет иметь вид:
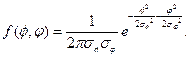
Величины ? и ? выражаются через среднеквадратичные отклонения в прошлой совокупности координат формулами:
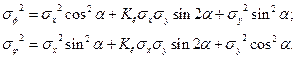
Полуоси эллипса определяются в этом случае следующим образом:
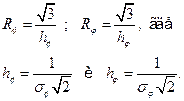
ВЫВОДЫ (Выводы по работе сделать самостоятельно).
ЗАДАНИЕ
На исполнение работы
Выполните расчет эллипса рассеяния центра электрических нагрузок шести потребителей в течение смены, длительностью восемь часов. Координаты потребителей определяются из выражений: xk = k0.5.(mn), yk = [k.(nm)]0.5. Тут k – порядковый номер потребителя, m – предпоследняя цифра перечня, n — последняя цифра перечня. Средние мощности потребителей, приведены в таблице. Наряду с этим Р5 = 2.Р1. Шестым потребителем есть ксеноновый светильник мощностью 20 кВт, режим работы которого выбрать самостоятельно. Мощность потребителей в течение смены изменяется по равномерному закону. Привести график эллипса с указанием размещения потребителей.
Выбрать сечения питающих линий и выполнить оценку оптимальности взятого ответа.
Таблица потребителей
| Номер Варианта | Мощности потребителей, кВт | |||
| P1 | P2 | P3 | P4 | |
ПРИМЕР Исполнения
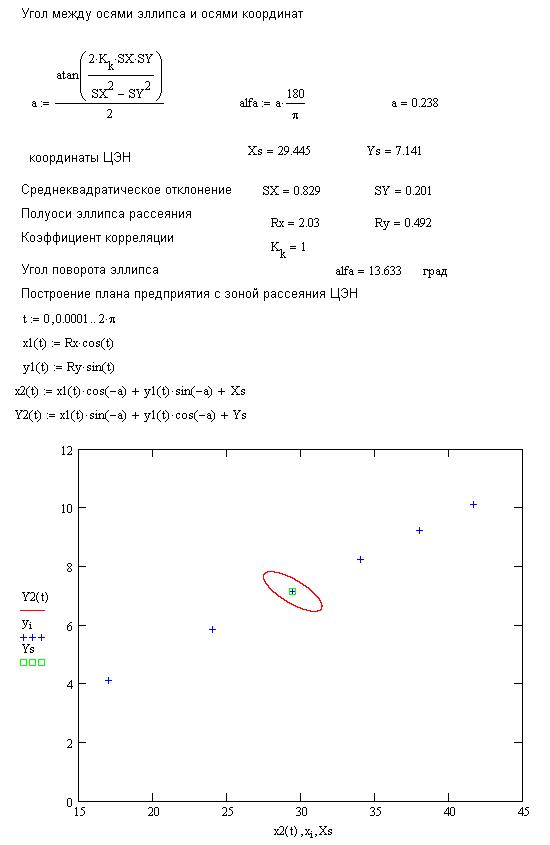
ВЫВОДЫ (Выводы по работе сделать самостоятельно).
Эллипс
Интересные записи:
- Определение уровня логистического обслуживания
- Определите исход лечения больного в соответствии с дефинициями воз и дайте рекомендации по диспансерному наблюдению. 11 глава
- Определите, какой процесс памяти (запоминание, сохранение, воспроизведение, узнавание) проявляется в описанных действиях
- Определите ложное суждение о роли религии в политике.