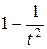q безотносительная величина отклонения среднего арифметического случайных размеров от среднего арифметического их математических ожиданий не превзойдет
—сумма случайных размеров не превзойдет
—разность случайных размеров не превзойдет
—отклонение суммы случайных размеров от суммы их математических ожиданий не превзойдет
При неограниченном повышении числа свободных опробований с однообразной возможностью появления события А в каждом опробовании
—относительная частота события А равна возможности этого события
q относительная частота события А сходится по возможности к возможности этого события
—относительная частота события А больше возможности этого события
—относительная частота события А меньше, чем
Закон солидных чисел есть теоретическим обоснованием
q выборочного способа
—статистической проверки догадок
—интегральной теоремы Лапласа
—формул комбинаторики
Закон солидных чисел гласит, что средняя арифметическая значений солидного числа случайных размеров
—есть случайной величиной
q пытается к постоянному числу
—пытается к случайной величине, имеющей показательное распределение
—пытается к случайной величине, имеющей биномиальное распределение
Центральная предельная теорема устанавливает условия, при которых сумма случайных размеров имеет распределение, близкое
—к показательному распределению
—к равномерному распределению
—к биномиальному распределению
q к обычному распределению
Из закона солидных чисел направляться, что на среднем результате действия солидного числа явлений действие одного из этих явлений
—не отражается
—очень сильно отражается
q мало отражается
—есть преобладающим
Лемма Маркова говорит, что хорошая случайная величина не превосходит — кратного математического ожидания с возможностью, большей
—
—
—
q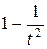 
Неравенство Чебышева говорит, что возможность отклонения случайной величины Х от ее математического ожидания на величину больше, чем
—
—
—
q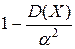 
Из теоремы Бернулли направляться, что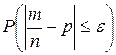 
—
— 
—
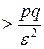
q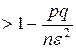 
В теореме Пуассона, входящей в закон солидных чисел,
— 
— 
—
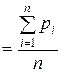
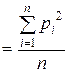
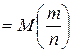
q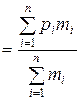 
В теореме Пуассона, входящей в закон солидных чисел,
— 
— 
—
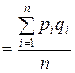
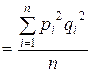
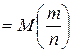
q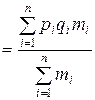 
Из теоремы Пуассона направляться, что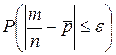 
—
— 
— 
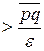
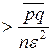
q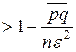 
Обобщенная теорема Чебышева говорит, что для случайных размеров, дисперсии которых ограничены сверху постоянным числом С, выполняется неравенство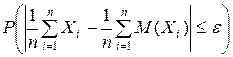 
— 
— 
—
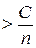
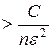
q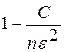 
В трактовке теоремы Чебышева, именуемой «Законом солидных чисел», утверждается, что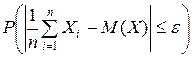 
—
—
— 
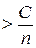
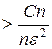
q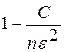
Для исполнения центральной предельной теоремы Ляпунова непременно условие
—число случайных размеров ограничено
—случайные размеры имеют показательное распределение
—случайные размеры распределены равномерно
q число случайных размеров неограниченно возрастают
Для исполнения центральной предельной теоремы Ляпунова непременно условие
—случайные размеры распределены равномерно
—случайные размеры имеют показательное распределение
q случайные размеры свободны
—число случайных размеров само собой разумеется
Для исполнения центральной предельной теоремы Ляпунова непременно условие
—случайные размеры распределены равномерно
—случайные размеры распределены нормально
q случайные размеры имеют конечные дисперсии и математические ожидания
—случайные размеры имеют биномиальное распределение
Для исполнения центральной предельной теоремы Ляпунова непременно условие
—случайные размеры имеют биномиальное распределение
—случайные размеры распределены равномерно
—число случайных размеров само собой разумеется
q ни одна из случайных размеров не выделяется по собственному действию на сумму
Из Леммы Маркова направляться, что
—
—
— 
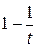
В группу теорем закона солидных чисел не входит
—теорема Бернулли
—теорема Пуассона
—обобщенная теорема Чебышева
q теорема Лапласа
В группу теорем закона солидных чисел не входит
—теорема Бернулли
—теорема Пуассона
—неравенство Чебышева
q теорема Коши
В группу теорем закона солидных чисел не входит
—неравенство Чебышева
—теорема Бернулли
—теорема Пуассона
q теорема Лагранжа
В неравенстве Чебышева
— 
—
— 
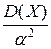
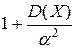
q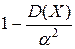
В предельной форме теорема Пуассона говорит, что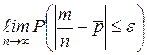 
=
—0
—
—
q 1
Предельная форма обобщенной теоремы Чебышева говорит, что
=
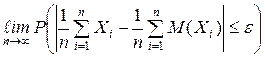—0
—
—
q 1
В теореме Пуассона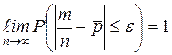 
величина имеется
—средняя геометрическая
—средняя интегральная
q средняя арифметическая взвешенная
—произвольная
Обобщенная теорема Чебышева выполняется для случайных размеров, для которых
—математические ожидания ограничены сверху
—возможности наступления мелки
—сумма возможностей больше единицы
q дисперсии ограничены сверху некоторым постоянным числом
В теореме Пуассона 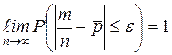величина есть
—возможностью наступления события А
—возможностью не наступления события А
q относительной частотой события А
—возможностью точного события
Математическое ожидание случайной величины Х равняется 3,2. Возможность того, что Х не превзойдет 4,0, больше, чем
q 0,20
—0,16
—0,43
—0,31
Дисперсия случайной величины Х равна 0,15. Громаднейшее отклонение случайной величины Х от ее математического ожидания М(Х) по полной величине с возможностью большей, чем 0,5, равняется
—0,31
q 0,55
—0,16
—0,49
Возможность наступления события А равна 0,6. Совершено 500 свободных опробований. Возможность того, что полная величина отклонения случайной величины Х – числа наступлений события от математического ожидания М(Х) не превзойдет 20, больше, чем
—0,5
—0,6
q 0,7
—0,8
Дисперсия случайной величины Х равна 0,6. Возможность того, что полная величина отклонения случайной величины Х от ее математического ожидания не превзойдет 1,2, больше, чем
—0,387
—0,222
q 0,583
—0,838
Возможность наступления события А в каждом опробовании равна 0,4. Проводится 200 опробований. Возможность того, что число наступлений события отклонится от его математического ожидания по безотносительной величине не более, чем на 16, больше, чем
—0,667
q 0,813
—0,765
—0,973
Дисперсия каждой из 2000 случайных размеров не превышает 9. Возможность того, что отклонение средней арифметической этих размеров от средней арифметической их математических ожиданий по полной величине не превышает 0,17, больше, чем
—0,45
q 0,55
—0,65
—0,75
ТЕМА 8. Выборочный способ.
В случае, если главная совокупность неоднородна, то метод отбора
—серийный
—фактически – случайный
q типический
—механический
Статистическое распределение выборки – это
q соответствие между вариационным и частотным последовательностями
—вариационный последовательность
—частотный последовательность
—число вариант в вариационном последовательности
Мерой колеблемости показателя около среднего значения в выборочной совокупности есть
—предельная неточность выборки
—выборочная часть
—коэффициент надежности
q выборочная дисперсия
Неточностью репрезентативности (выборки) именуется
—неточность при вычислении черт выборочной совокупности
q отклонение черт выборочной совокупности от соответствующих черт главной совокупности
—неточность при вычислении черт главной совокупности
—среднее квадратическое отклонение
Надежностью оценки числовой характеристики главной совокупности именуется
q возможность попадания данной характеристики в доверительный промежуток
—отношение предельной неточности выборки к средней неточности
—доверительный промежуток
—точность оценки
В выборочном способе гистограмма – это графическая иллюстрация
—функции распределения
—функции распределения
—плотности распределения
q статистического распределения выборки при интервальном задании вариационного последовательности
—закона распределения дискретной случайной величины
К числовым чертям выборочной совокупности относится
—предельная неточность выборки
—главная часть
—коэффициент надежности
q выборочная часть
Средняя неточность выборки – это
—выборочная средняя
—выборочное среднее квадратическое отклонение
q среднее отклонение чёрта выборочной совокупности от соответствующей чёрта главной совокупности
—выборочная дисперсия
Доверительный промежуток – это промежуток, в который с надежностью попадает
q черта главной совокупности
—черта выборочной совокупности
—значение изучаемого показателя главной совокупности
—значение изучаемого показателя выборочной совокупности
Выборочная средняя – это
—значение изучаемого показателя, выбранное из середины вариационного последовательности
q среднее взвешенное значение показателя в выборочной совокупности
—среднее арифметическое всех значений показателя в выборочной совокупности
—среднее взвешенное квадратов отклонений значений показателя около среднего
Выборочная средняя равна
— 
— 
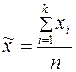
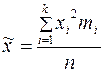
q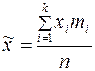 
— 
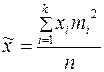
Величина количества выборки зависит от
q требуемой надёжности и точности результатов
—главной дисперсии
—выборочной средней
—главной средней
В формуле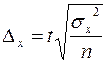 
коэффициент t именуется
—коэффициентом выборки1# коэффициентом надежности
—показателем выборки
—точностью оценки
При повторном фактически – случайном отборе предельная неточность выборки зависит от
—количества главной совокупности
—главной дисперсии
q количества выборочной совокупности
—выборочной средней
При серийном отборе под количеством выборки понимается
—среднее количество элементов в серии
—количество элементов в одной из серий
—громаднейшее количество элементов во всех сериях
q количество серий, выбранных из общего числа серий
Выборочный способ опирается на
—теорему Бернулли
—теорему Пуаcсона
—лемму Маркова
q теорему Чебышева –Ляпунова
При повторном отборе зарегистрированные и обследованные единицы
q снова возвращаются в главную совокупность и опять смогут учавствовать в будущем отборе
—в главную совокупность не возвращаются
—в главную совокупность возвращаются, но учавствовать в будущем отборе не смогут
—помечаются особым знаком
При бесповторном отборе зарегистрированные и обследованные единицы
—возвращаются в главную совокупность
q не возвращаются в главную совокупность
—возвращаются в главную совокупность и смогут учавствовать в будущем отборе
—в главную совокупность возвращаются, но учавствовать в будущем отборе не смогут
При серийном методе отбора в выбранной серии проводится
q целое наблюдение
—выборочное наблюдение
—наблюдение первых n элементов
—наблюдение последних n элементов
Типический метод отбора используется в тех случаях, в то время, когда главная совокупность
—складывается из малого числа элементов
q неоднородна
—однородна
—неупорядочена
К методам отбора не требующим разделения на группы, относятся
—случайный и типический методы отбора
—типический и серийным методы отбора
—механический и серийный методы отбора
q случайный и механический методы отбора
К методам отбора требующим разделения на группы, относятся
—случайный и типический методы отбора
q типический и серийным методы отбора
—механический и серийный методы отбора
—случайный и механический методы отбора
Одной из главных задач выборочного способа есть
—целое наблюдение
q определение нужной численности выборки
—подсчет количества элементов главной совокупности
—изучение изменчивости элементов главной совокупности
Выборочная дисперсия по средней – это
—среднее взвешенное значение квадратов показателей в выборке
q среднее взвешенное квадратов отклонений значений показателя около выборочной средней
—среднее значение показателя в выборке
—громаднейшее значение показателя
Выборочную (по средней) дисперсию возможно вычислять по формуле
— 
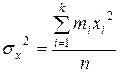
q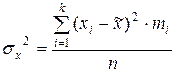 
— 
— 
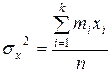
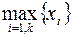
При типическом отборе численность каждого типа в выборке
—однообразна
—равна количеству выборки
—обратно пропорциональна количеству типа в главной совокупности
q пропорциональна количеству типа в главной совокупности
Частотный последовательность это
—совокупность выборочных значений показателя
—совокупность квадратов выборочных значений показателя
q упорядоченная последовательность частоты появлений разных значений показателя
—соответствие между числом появления и значениями признака этих значений
Предельная неточность выборки связана со средней неточностью формулой
— 
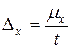
q
—
—
Предельная неточность показывает
—мельчайшее отклонение выборочной средней от главной средней
—среднее отклонение выборочной средней от главной средней
q громаднейшее отклонение выборочной средней от главной средней
—громаднейшую дисперсию
Упорядоченная последовательность вариант именуется
—частотным рядом
—числовым рядом
q вариационным рядом
—функциональным рядом
В выборочном способе полигон частот – это графическая иллюстрация
—функции распределения
—плотности распределения
—статистического распределения выборки при интервальном задании вариационного последовательности
q статистического распределения выборки при задании вариационного последовательности в виде последовательности вариант
При возрастании количества выборки n предельная неточность выборки
q значительно уменьшается
—возрастает
—не изменяется
—пытается к бесконечности
При повышении надежности предельная неточность выборки
—значительно уменьшается
q возрастает
—не изменяется
—пытается к 0
С возможностью возможно утвердить, что при большом количестве выборки отличие между и не превзойдет
—коэффициента надежности t
—средней неточности выборки
—дисперсии
q предельной неточности выборки
Величина количества выборки n зависит от
q требуемых надёжности и точности результатов
—изучаемого показателя
—главной средней
—главной доли
При выборочном обследовании 100 единиц совокупности, взятой фактически – случайным методом, были взяты следующие эти:
| x | 10-20 | 20-30 | 30-40 | 40-50 |
| m |
Выборочная средняя равна
—28
—29
—30
q31
При выборочном обследовании 100 единиц отыскано среднее квадратическое отклонение . С возможностью, равной 0,9973, предельная неточность выборки по средней при повторном отборе равна
—0,2
—0,02
q 0,06
—0,6
При выборочном обследовании стажа работы 100 сотрудников учреждения фактически – случайным методом отбора взяты эти:
| x | 0-10 | 10-20 | 20-30 | 30-40 |
| m |
Часть сотрудников, имеющих стаж работы 20 лет и более, равна
—0,2
q 0,4
—0,3
—0,1
Часть стандартных подробностей в выборочной совокупности количеством в 100 штук, взятой методом повторного, фактически – случайного отбора, равна 0,8. С возможностью 0,9973 предельная неточность выборки по доле равна
—0,08
q 0,12
—0,8
—1,2
При выборочном обследовании 80 единиц совокупности, взятой методом фактически – случайного отбора, были взяты следующие эти:
| x | 5-15 | 15-25 | 25-35 | 35-45 |
| m |
Выборочная средняя равна
—28,6
—26,6
q 25,6
—23,6