Применяемые контрольно-измерительные материалы разрешили установить уровень сформированности метапредметных результатов у обучающихся 5-х классов в начальной школе в соответствии с требованиями федерального национального образовательного стандарта. Главной целью диагностической работы есть оценка свойства пятиклассников использовать купленные в начальной школе метапредметные умения для ответа разнообразных задач учебного и практического характера, сконструированных на содержании учебного предмета Математика.
На протяжении проведения тестирования пятиклассников была возможность:
— проверить метапредметные умения обучающихся на содержании учебного предмета математика, и умения и предметные знания за начальный курс математики, нужные для успешного исполнения задания;
— выяснить уровень овладения главными видами учебной деятельности, среди которых: моделирование обстановки, обнаружение математических зависимостей в окружающем мире, планирование хода ответа задачи, оценка полноты и правильности исполнения действий, выделение и поиск нужной информацим, установление причинно-следственных связей, постановка вопросов.
Контрольно-измерительные материалы складывались из 7 заданий (с №8 по № 14) составленных для четырех вариантов, каковые встраивались в неспециализированную работу. В мониторинговых обследованиях употреблялись задания трех вариантов.
Они контролировали метапредметные результаты (уровень сформированности УУД): регулятивные УУД — планирование, оценка; познавательные УУД — общеучебные (выделение и поиск информации, знаково-символическое моделирование), логические (классификация, установление причинно-следственных связей), коммуникативные (постановка вопросов). Обучающимся предлагались учебные либо практические задачи (обстановки) математического характера в которых нет явного указания на метод исполнения, а обучающийся сам обязан выбрать данный метод из комплекта известных ему. В некоторых случаях требовалось интегрировать два-три изученных метода либо обучающийся сам обязан сконструировать метод ответа. их выполнение и Содержание заданий предполагало проявление у пятиклассников перечисленных УУД, наличие предметных умений и знаний (что снабжает успех исполнения данных заданий).
В КИМ были включены два типа заданий: 6 заданий с выбором ответа (ВО) и 1 задание (№12) с кратким ответом (КО). При исполнении задания с выбором ответа от обучающегося требовалось отметить один верный ответ из четырех предложенных вариантов либо пара верных ответов из шести предложенных вариантов ответов. В задании с кратким ответом требовалось записать итог действия (число).
Контролируемые метапредметные предметная основа и результаты (элементы предметного содержания) представлены в таблице:
ФГОС НОО содержит четкие требования к уровню подготовки обучающихся, оканчивающих начальную школу, по всем разделам главной образовательной программы (включая Программу формирования УУД и программы учебных предметов, а также предмета «Математика»). Кроме этого Стандартом выяснены главные виды учебной деятельности, каковые делают учащиеся в ходе освоения курса математики, и список компонентов, характеризующих математическое развитие выпускников начальной школы. В данной связи задания составлялись с учетом проявления при их исполнении первым делом метапредметных (сформированность УУД), а после этого и предметных (математических) результатов обучения.
Уровень сформированности регулятивных УУД проверялся на следующем математическом содержании: планирование в 1 и 3 вариантах на разделе Геометрические размеры, во 2 и 4 вариантах на разделе Работа с текстовыми задачами; оценка во всех вариантах на разделе величины и Числа. Познавательных УУД: логические (классификация, установление причинно-следственных связей) на разделах величины и Числа, Арифметические действия, фигуры , общеучебные (знаково-символическое моделирование, выделение и поиск информации) на разделах Работа с текстовыми задачами (1, 3 вариант), Арифметические действия (2, 4 варианты), Работа с информацией. Коммуникативных УУД (постановка вопросов) на разделе Работа с текстовыми задачами. Выбор разделов обусловлен спецификой содержания начального курса математики, значением и ролью данной дисциплины в достижении метапредметных результатов. Имеется задания, в которых одинаковый метапредметный итог (конкретное УУД) проверялся в различных вариантах на различном математическом содержании (к примеру, задание №8). Таковой подход к составлению заданий был осуществлен намеренно, что разрешает при анализе исполнения работы диагностировать затруднения обучающихся не только (и не столько) в метапредметности, сколько в предметной составляющей.
направляться подчернуть, что процент исполнения всех заданий по всем трем вариантам низок (не превышает 35%). самые трудными для исполнения были задания 8 в третьем варианте, 9 во всех трех вариантах и 10 в первом и третьем вариантах.
Дадим чёрта исполнения каждого некоторых заданий.
Задание 8 было направлено на обнаружение умения делать классификацию объектов (логические УУД), основание классификации обучающимся следовало установить самостоятельно. оптимальнее это задание было выполнено во втором варианте (38,6%), где требовалось выбрать лишнее числовое выражение, существенно ниже процент исполнения этого задания в 1 варианте (24,0%) на фигурах и в 3 варианте (18,2%) на числах. Громадный разброс по вариантам в исполнении данного задания говорит о том, что обучающиеся достаточно отлично могут обнаружить основание для классификации числовых выражений, фигур и не могут выбирать основание для классификации многозначных чисел, что, быть может, связано с освоением темы Нумерация многозначных чисел (умения выделять неспециализированное число единиц первого и второго классов).
В задании 9 диагностировалось умение к заданной знаково-символической модели подбирать текстовые задачи (вариант 1 и 3) и числовые выражения (вариант 2). Анализ исполнения данного задания на различном предметном содержании разрешает сделать вывод, что обучающиеся испытывают затруднение как при работе с текстовыми задачами, так и с числовыми выражениями. Это скорее связано не с освоением предметного содержания, а с недостаточным уровнем сформированности умения трудиться с графическими и знаково-символическими моделями (не умение соотносить знаково-символическую и вербальную модели задачи, фиксацию изученного метода в знаково-символической форме с числовым выражением).
Задание 10 было направлено на диагностику уровня сформированности регулятивного УУД — оценка, где требовалось оценить предлагаемый выбор чисел с заданным свойством из указанной части натурального последовательности. Данное задание было выполнено неоднородно. Больший процент его исполнения (31,6%) отмечается во 2 варианте, где по заданному свойству выбирались трехзначные числа; затруднения испытали обучающиеся 1 и 3 вариантов (процент исполнения 19,8 и 16,0 соответственно), в которых по заданному свойству следовало выбрать двузначные числа. Допустимо в этих вариантах на итог исполнения повлияли плохо организованные предметные умения.
Задание 11 диагностировало умение планировать (регулятивное УУД) при ответе текстовой задачи во втором варианте и вычислении площади прямоугольника в первом варианте и периметра прямоугольника в третьем варианте. Задание выполнено во всех вариантах достаточно ровно (средний процент исполнения по трем вариантам 30,8), что разрешает сделать вывод о сформированности данного метапредметного умения на среднем уровне.
Задания 12, диагностирующее познавательное УУД (выделение и поиск информации); задание 13 — коммуникативное УУД (постановка вопросов), задание 14 — познавательное УУД (установление причинно-следственных связей) фактически выполнены на одном уровне (процент исполнения по вариантам колеблется от 22% до 28%), что говорит о сформированности перечисленных УУД на уровне ниже среднего.
Количественный анализ метапредметных результатов (универсальных учебных действий) представлен в таблице.
| Метапредметный итог (универсальные учебные действия) | Процент исполнения заданий по вариантам | Уровень сформированности | |||
| 1 вариант | 2 вариант | 3 вариант | среднее значение | ||
| Классификация | 24,0 | 38,6 | 18,2 | 26,9% | ниже среднего |
| Знаково-символическое моделирование | 13,7 | 14,5 | 18,6 | 15,6% | низкий |
| Оценка | 19,8 | 31,6 | 16,0 | 22,5% | ниже среднего |
| Планирование | 32,4 | 30,4 | 29,7 | 30,8% | выделение |
| информации и средний Поиск | 27,4 | 22,2 | 24,7 | 24,8% | ниже среднего |
| Постановка вопросов | 28,3 | 26,3 | 24,1 | 26,2% | ниже среднего |
| Установление причинно-следственных связей | 24,3 | 26,3 | 26,3 | 25,6% | ниже среднего |
Низкий уровень сформированности УУД характеризуется не сильный пониманием учебной цели, умением механически прочесть данные, воспринять ее фрагментарно, частично решить самая простую элементарную учебную задачу. Уровень ниже среднего так же характеризуется не сильный удержанием учебной задачи, умением принимать данные лишь фрагментарно, выделить лишь несущественные факты, выстроить простейшее умозаключение, решить одну несложную учебную задачу. Эти уровни мешает успешному обучению в главной школе.
Средний уровень сформированности УУД характеризуется умением удерживать учебную задачу, принимать данные целостно, определять значительные связи, частично осуществлять воздействие самоконтроля, обнаружить кое-какие неточности, разбирать и составлять несложные модели объектов и явлений Этот уровень есть удовлетворительным и достаточным для освоения обучающимся программы главной школы.
Отмечается отсутствие опрощеных, каковые бы показали уровень сформированности исследуемых УУД (классификация, знаково-символическое моделирование, оценка, планирование, выделение и поиск информации, постановка вопросов, установление причинно-следственных связей) на:
— уровне выше среднего, что характеризуется умением удерживать учебную задачу, планировать ее исполнение, осуществлять преобразование и поиск информации, делать действия моделирования, осуществлять спектр логических действий, включая анализ, синтез, сравнение, обобщение, выделение значительных связей. Обучающийся может определять несложные причинно-следственные связи, обнаружить неточности и устанавливать кое-какие обстоятельства их появления. Этот уровень есть оптимальным для освоения обучающимся программы главной школы.
— большом уровне, характеризующимся свойством принимать и сохранять учебную цель и задачу, планировать ее реализацию, осуществлять контроль и оценивать собственные действия, выделять и фиксировать необходимую информацию, систематизировать, сопоставлять, разбирать и обобщать данные, трактовать и преобразовывать ее, обладать широким спектром логических операций и действий, включая действия моделирования решения и общие приёмы задач, мочь строить логическое рассуждение, устанавливать причинно-следственные связи, осуществлять анализ объектов с выделением значительных и несущественных показателей, проводить сравнение и классификацию, выделять и фиксировать необходимую информацию, растолковывать и обосновывать факты Этот уровень есть самый благоприятным для освоения обучающимся программы главной развития и школы интеллектуального и творческого потенциала личности.
Средние значения сформированности исследуемых УУД представлены в диаграмме:
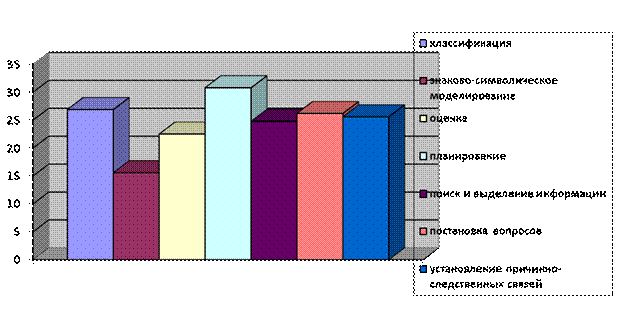
Вероятные обстоятельства затруднений при исполнении заданий по рекомендации и математике по их предупреждению
| № задания | Контролируемые метапредметные умения (УУД) | Средний % исполнения по трем вариантам | Обстоятельства затруднения | Советы для преподавателя |
| Классификация | 26,9% | Успешность исполнения данного задания была обусловлена уровнем владения предметными результатами. В 1 варианте умениями распознавать фигуры на базе их значительных показателей; обнаружить фигуры, владеющие заданным свойством (наличие прямых, острых, тупых углов, равных сторон). Во 2 варианте умением определять порядок действий в выражениях со скобками и вычислять в пределах 100. В 3 варианте пониманием позиционной записи многозначного числа. Обстоятельства затруднения, появившиеся при исполнении данного задания, связаны с освоением темы Нумерация многозначных чисел (умения выделять неспециализированное число единиц первого и второго классов) в третьем варианте. Затруднения при исполнении задания первого варианта (необходимо было выбрать треугольник, в котором нет прямого угла) обусловлена недостаточной сформированностью в начальной школе представления о прямом угле, умении его обнаружить в фигурах . Полагаем, что недостаточная математическая подготовка обучающихся согласно данным темам оказала влияние на успех исполнения задания в целом, что говорит о зависимости проявления метапредметных умений от уровня владения умениями и предметными знаниями. | Классификация это такое УУД, которое начинает формироваться у детей еще в дошкольный период и длится в начальной школе. Первоклассники делают классификацию объектов (по большей части фигуры ) по очевидно известный показателям (форме, цвету, размеру). К окончанию начальной школы обучающиеся должны мочь самостоятельно устанавливать основание для классификации (наличие у фигур прямых углов либо равных сторон; у выражений однообразных арифметических действий либо числовых значений и пр.). Но средний процент исполнения задания говорит о недостаточном уровне сформированности данного УУД. В данной связи преподавателям целесообразно составлять либо подбирать задания на классификацию разных объектов (среди них и математических) с указанием и без указания основания (показателя) классификации для систематического применения в учебной деятельности пятиклассников. Включать такие задания не только на уроках математики, но и других предметах. А для успешного исполнения заданий для того чтобы характера на математическом содержании нужно обратить внимание на более качественное формирование математических понятий, обозначенных учебной программой и умений в применении взятых знаний при ответе разных (среди них и практико-ориентированных) заданий. Нужна коррекция умений и знаний обучающихся по темам Нумерация многозначных чисел и фигуры . | |
| Знаково-символическое моделирование | 15,6% | Относительно низкая решаемость задания предположительно возможно растолкована нестандартностью его формулировки. Где от обучающихся к заданному в знаково-символической форме равенству (фиксирующему или метод ответа задачи (вариант 1 и 3), или метод вычисления (вариант 2)) требовалось подобрать все подходящие варианты ответов из шести предложенных. Для этого нужно было выполнить анализ каждой из задач (в 1 и 3 вариантах) и каждого числового выражения (во втором варианте) и соотнести знаково-символическую и вербальную модели задачи либо выражения. Напомним, что такие задания в книжках математики начальной школы фактически отсутствуют, что растолковывает недостаточность опыта их исполнения обучающимися. | Обучение по действующим программам математики в начальной школе предполагает использование различных знаково- символических средств (буквы, цифры, схемы и пр.). Для успешного обучения у выпускников начальной школы должны быть организованы действия кодирования (замещения) и декодирования (считывание информации), умения применять готовые модели, строить модели и схемы для ответа задач. Процент исполнения задания свидетельствует, что у обучающихся на низком уровне организовано данное УУД. В данной связи в уроки математики нужно включать задания на декодирование информации, на построение моделей для ответа не только текстовых задач , но и решения уравнений, исполнения вычислений в числовых выражениях и пр. Приведем пример задания: Подобрать выражение, значение которого возможно вычислить следующим методом: (? — ?) • ? = ? • ? — ? • ?. | |
| Оценка | 22,5% | Данное задание потребовало от пятиклассников выполнить оценку ответов учеников некой школы, каковые выбирали числа с заданным свойством из указанной части натурального последовательности. Затруднения вызвали задания 1 и 3 вариантов при выборе двузначных чисел. Возможно высказать предположение, что главная трудность у обучающихся связана с умением соотнести правило, по которому составлена заданная числовая последовательность с числовым рядом, найти неточности и оценить предложенные варианты ответов. Практико-ориентированная формулировка задания потребовала от школьников внимания, понимания смысла математических понятий четное число, нечетное число и взаимоотношений больше/ меньше на…, умений сравнивать двухзначные и трехзначные числа, что определяет особенность задания и повышает трудность его исполнения. | Работа по формированию оценки и действий контроля у обучающихся обязана вестись на всех уроках. Но отмечаем, что у большей части выпускников начальной школы они организованы слишком мало. В данной связи преподавателям нужно вести целенаправленную работу по формированию контрольно-оценочной самостоятельности школьников. Структура действия оценки, уровни сформированности оценки отлично прописаны в книге Как проектировать универсальные учебные действия в начальной школе. От действия к мысли (пособи для преподавателя, под ред. А.Г. Асмолова, М., Просвещение, 2011, С.80 — 85). Так же нужно включать в уроки математики задания на оценку готовых ответов как собственных, так и одноклассников; задания типа: Ученики лесной школы составляли задачи, для ответа которых нужно выполнить действия в таком порядке: сложение, умножение, вычитание. Кто из учеников правильно составил задачу?. | |
| Планирование | 30,8% | Задание было сконструировано на содержании разделов Геометрические размеры (1 и 3 варианты) и Работа с текстовыми задачами (2 вариант). Процент исполнения данного задания выше. Но у пятиклассников появились кое-какие затруднения в определении шагов метода вычисления периметра прямоугольника. | Преподавателям нужно продолжить работу по формированию регулятивного УУД планирование при работе как с текстовыми задачами, так и математическим содержанием вторых разделов программы. | |
| выделение и Поиск информации | 24,8% | Задание выстроено на содержании разделов Работа с информацией и Арифметические действия. Особенность задачной формулировки заключалась в том, что обучающиеся должны были выделить нужную информацию из предложенного содержания энциклопедии ( часть информации была представлена в заглавии энциклопедии), а после этого для ответа на вопросы выполнить арифметические действия. Трудность в исполнении данного задания обусловлена, неумением обучающихся связывать взятую данные в единое целое и на базе ее анализа делать арифметические действия. | Для успешного формирования данного универсального учебного действия обучающимся направляться предлагать разные виды текстов (целые и несплошные). Формулировать задания так, дабы их исполнение было связано с выбором информации , выделением значительных сведений. Пример: Выполни задания, пользуясь содержанием энциклопедии «111 страниц о деревьях-долгожителях». Обрати внимание, что любая статья начинается с новой страницы! На страницах, номера которых заканчиваются цифрой 4 (4, 14 и т. д.), помещены фотографии – по четыре на странице. Потом идет содержание (страницы и название статей). На какой странице заканчивается статья о баобабе? какое количество всего страниц в энциклопедии? какое количество всего фотографий в энциклопедии? какое количество страниц текста без фотографий посвящено сосне? и т.д. | |
| Постановка вопросов | 26,2% | Для проверки умения задавать вопросы обучающимся был предложен текст, содержащий числовые эти, к которому нужно было подобрать все вопросы, обращающие его в текстовую задачу. Относительно низкая решаемость возможно обусловлена следующими факторами: а) неумением к тексту задавать вопросы б) неумением разбирать текст, выделять искомое и данные; устанавливать связь между ними; б) недостаточным опытом исполнения аналогичных заданий к концу 4-го класса. | Постановка вопросов всегда приводит к затруднению у обучающихся начальной школы. В данной связи нужна целенаправленная работа по обучению обучающихся осознавать суть прочтённого, задавать вопросы, применяя приемы разработки развития критического мышления на базе письма и чтения (к примеру, прием узкие и толстые вопросы), приемы разработки продуктивного чтения и пр. Приведем пример задания: Прочти рассказ Риты о собственной семье: «Мне 8 лет. Самая старшая в отечественной семье – бабушка, ей 68 лет. Дед младше бабушки на 2 года. Моя сестра Лена в 2 раза старше меня, а мой брат Денис в 2 раза младше меня. В то время, когда появился отец, дедушке было 25 лет. Мама младше папы на 3 года». На эти вопросы возможно ответить, не делая арифметических действий. а) какое количество лет маме? б) какое количество детей в семье? в) Кто старше: Лена либо Данил? г) Во какое количество раз Рита старше Данила? д) На какое количество лет Рита старше Данила? | |
| Установление причинно-следственных связей | 25,6% | Задание было сконструировано на содержании величины и раздела Числа. Успешность его исполнения обусловлена предметными умениями записывать и сравнивать величины (масса, время, протяженность), различать единицы измерения размеров, переводить из одних единиц измерения в другие (в соответствии с обстановкой). Трудность задания заключалась в том, что обучающимся нужно было на базе обрисованной обстоятельства установить следствие. Напомним, что такие задания в книжках математики отсутствуют и низкий процент исполнения задания возможно еще обусловлен отсутствием опыта исполнениях заданий для того чтобы вида на математическом содержании. | Для создания данного УУД нужно включение намерено сконструированных заданий в учебно-познавательную деятельность обучающихся на всех предметах учебного замысла. Пример упражнения на математическом содержании : Отметь задания, с которыми не справится ученик, если он знает, что час продолжается продолжительнее 60 секунд, но не знает на какое количество продолжительнее: А) сравни 2 ч и 200 мин Б) сравни 2 ч и 2 мин В) 3 ч – 18 мин Г) 3 ч 20 мин – 2 ч 15 мин Д) 25 мин + 4 мин 18 с Е) 5 ч 35 мин + 55 мин |
Так, на базе результатов исполнения заданий возможно сделать вывод, что обучающиеся испытывают громадные трудности фактически во всех заданиях (на установление причинно-следственных связей, выделение и поиск информации, классификацию, постановку вопросов, оценку, знаково-символическое моделирование). Низкий процент исполнения этих заданий может свидетельствовать о недостаточной работе педагогов начальной школы в этом направлении. Частично это обусловлено тем, что школьные книжки (среди них и книжки математики) различных авторов не предполагают системной работы по формированию у обучающихся УУД.
Задания для диагностики метапредметных результатов составленные на математическом содержании попадают в категорию сложных для обучающихся еще и по причине того, что требуют от обучающихся применения не только организованных универсальных учебных действий, но и вариативности мышления и проявления гибкости (выбор нескольких вариантов ответа), обобщения и сравнения (обнаружение последовательности чисел в последовательности), умения планировать деятельность согласно решению задачи, и умений и предметных знаний (выявлять эти, взаимосвязь и искомые между ними, знания единиц времени, длины, соотношений и массы между ними, определять порядок действий в выражениях со скобками и вычислять в пределах 100, обнаружить фигуры, владеющие заданным свойством, обнаружить площадь и периметр прямоугольника и пр.).
Для устранения «пробелов» в формировании УУД у обучающихся в главной школе направляться советовать преподавателям включать в обучение практико-ориентированные задания; наряду с этим направляться выяснять сущность применяемых в них понятий. Предлагать обучающимся для исполнения на уроках задания из вторых источников (не книжек), в то время, когда требуется выяснить часть информации из схемы, таблицы, графика, текста. Такие задания являются базой для создания метапредметных результатов освоения программы по новым образовательным стандартам (ФГОС ООО); до тех пор пока в действующих книжках их слишком мало. Кроме этого возможно советовать преподавателям не пропускать такие ответственные этапы работы над математическими заданиями, как анализ условия задания, методы представления данных, работа по готовым ответам и их оценка, составление обратных задач, изменение данных в задаче, включение в процесс обучения заданий с недостающими и лишними данными.
Так же положение может исправить применение проектных, комплексных, интегрированных заданий для обучающихся главной школы, исполнение которых требует не только предметных (умений и математических знаний), но и универсальных учебных действий, смекалки, творчества, изобретательности, знаний из вторых предметных областей (литература, природоведение, информатика, разработка). Учителя, родители и руководство школы должны отлично осознавать назначение таких заданий. Это не усложнение программы и не дополнительная нагрузка на обучающегося, а неповторимая возможность формирования у обучающихся целостного представления о мире и одно из условий успехи метапредметных результатов, составляющих базу главной компетенции школьника «умения обучаться».
Нужна четкая организация групповой работы школьников. В частности, крайне важны такие формы работы, как организация обоюдной проверки заданий, обоюдные задания групп. Работа в группе оказывает помощь ребенку осмыслить учебные действия. Помимо этого, работа в группе разрешает дать ученикам эмоциональную и содержательную помощь, без которой многие по большому счету не смогут включиться в неспециализированную работу класса, к примеру робкие либо не сильный ученики. Групповая работа обучающихся 5 класса предполагает собственные правила: нельзя принуждать детей к групповой работе, совместная работа не должна быть больше 10—15 мин, чтобы не было утомления и снижения эффективности. Для групповой работы возможно применять время на уроках. Но возможно завлекать другие формы, к примеру проектные задания.
В ходе обучения математике больше обращать внимание на следующие моменты:
– в любой момент ли нужно правильное вычисление либо достаточно оценить выражение, прогнозировать итог;
– пристально ли прочтено учеником задание;
– допустимо ли существование нескольких ответов в одном задании (в большинстве случаев, готовые КИМ содержат задания с выбором ответа, из которых лишь один верный, что формирует выполнения заданий и шаблонность мышления по математике);
– вероятны ли лишние данные в условии задачи, что разрешило бы её решить не какое количество методами либо обосновать выбор действия.
Нужно обратить особенное внимание на комплексную реализацию программы Чтение. Работа с текстом на всех подряд учебных предметах, направленной на развитие читательских действий, таких как поиск информации, выделение нужной для ответа практической либо учебной задачи информации, систематизация, сопоставление, обобщение и анализ имеющихся в тексте сведений, преобразование и интерпретация информации.
Нужно кроме этого применение современных образовательных разработок деятельностной направленности, каковые разрешают целенаправленно и системно вырабатывать регулятивные, коммуникативные, познавательные и личностные УУД.
Для определения уровня достижений обучающимися метапредметных результатов, мониторинга и проведения диагностики сформированности УУД нужно применение КИМ, спроектированных на предметном содержании различных учебных дисциплин (к примеру, русский язык, математика), комплексных работ, конечно КИМ отвлеченных от предметной составляющей. Таковой подход разрешит распознать зависимости между метапредметными и предметными результатами и более определить уровень достижений каждого обучающегося.