Приступая к ответу задачи необходимо помнить, что условие задачи обрисовывает конкретную обстановку, которая включает объекты (участники происходящего), действия с их участием и итог этих действий. Все это должно выделяться на самом первой стадии ответа задач по физике, что именуется анализом условия задачи.
Опыт говорит необходимость выделять по условию задачи объекты действий, сами действия и их итог. В данной связи станет допустимо сказать о физических размерах, относящихся к объектам (к примеру, масса тела, размеры, плотность и т.д.) либо процессам и действиям (к примеру, скорость для перемещения, изменение энергии для перехода из одного состояния в второе и др.) и законах (и правилах либо определениях, но не о готовых формулах), отражающих связь этих размеров. Наряду с этим происходит научное объяснение и теоретическое раскрытие конкретных фактов, затронутых в задаче, а, следовательно, и логически верное выведение одних суждений (промежуточных выводов) из вторых (начальных положений).
Наряду с этим запись формул происходит как математическая форма выражения распознанных законов в тех обозначениях, каковые были или заданы в условии, или введены нами по ходу анализа разглядываемой в задаче обстановки. Принципиально важно выделить, что запись формул обязана сопровождаться словесным повторением содержания записываемых обозначений и уточнением доводов, поясняющих возможность применения в данной задаче того закона (принципа, зависимости и пр.), что выражается данной формулой. В данной связи подчеркиваем, что запоминание формулы должно сводиться не к запоминанию последовательности входящих в нее обозначений как определенных букв, а к выучиванию вида зависимости между определенными физическими размерами, могущими быть обозначенными по-различному. Несложнее говоря: пишем букву, а в уме держим содержание этого обозначения.
Так, ответ задачи сводится к следующей начальной последовательности:
— распознание объектов, участвующих в создании обстановки, обрисованной в условии;
— выделение из теоретического материала элементов физических знаний (законов, определений и пр. связей), обрисовывающих либо относящихся к выделенным объектам;
— выбор (соотнесение и разграничение) обозначений соответствующих определенным выше законам (определениям и др. элементам теории) физических размеров, констант и пр.;
— математическая запись выражений (формул), применительно к конкретной обстановке.
Увидим, что формулы в общем виде упоминаются на втором этапе, например, при формулировке какого-либо закона (к примеру, закона прямолинейного перемещения тела с постоянным ускорением). Формулы, полученные при ответе конкретной задачи смогут быть двух типов: А) формулами неспециализированных закономерностей (определений и пр.), записанными с учетом применяемых в данной задаче обозначений либо «неспециализированные формулы», В) формулами, взятыми на базе подстановки в формулу типа А, обрисовывающую процесс, данных, относящихся к конкретному выбранному состоянию либо «конкретные равенства» (к примеру, 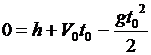 , где — значение координаты камня в момент времени , — все время перемещения камня, т.е. выбрано конкретное положение, точка на графике – одна из множества вероятных точек на траектории).
, где — значение координаты камня в момент времени , — все время перемещения камня, т.е. выбрано конкретное положение, точка на графике – одна из множества вероятных точек на траектории).
 Методические указания. Итак, приступая к ответу задач, нужно, в первую очередь, четко и светло разобраться в конкретной обстановке, обрисованной в задаче. Уместно сделать схематический чертеж, на котором указать искомые и данные величины применительно к состояниям, затронутым в задаче. Рекомендуется сказать о задаче по схеме:
Методические указания. Итак, приступая к ответу задач, нужно, в первую очередь, четко и светло разобраться в конкретной обстановке, обрисованной в задаче. Уместно сделать схематический чертеж, на котором указать искомые и данные величины применительно к состояниям, затронутым в задаче. Рекомендуется сказать о задаче по схеме:
что имеется ® что происходит ® что делается результатом.
Традиционно, эти будем располагать в столбик слева от ответа, сходу переводя их в совокупность СИ. Крайне важно выполнять единство обозначений в течении всего оформления задачи.
Задача по физике считается решенной, в случае, если взята неспециализированная формула, высказывающая искомую величину через эти и узнаваемые постоянные размеры! расчёты и Математические выкладки составляют второстепенную часть ответа задачи и имеют место на более большом уровне доведения ответа до окончательного результата. В противном случае говоря, при ответе задач по физике более ответственным есть распознание и выделение физической сущности явлений, их связей, использование фундаментальных законов физики к конкретной обстановке и т.д., чем демонстрация умения подставлять числовые значения в формулу и обнаружить значение выражений, не вникая в их смысловую нагрузку в задаче!
Ответ задач по кинематике сводится к установлению формы и вида перемещения (ответа на вопрос «Как движется тело?»), записи закона перемещения, нужных формул-определений, получению конкретных равенств с учетом данных задачи и выражению из них искомых размеров.
Методические указания. Ответ задач по физике должно непременно содержать рисунок (чертеж), делающий функцию краткого и схематического изложения содержания условия задачи (наглядное изображение конкретной обстановке). Причем, рисунок сделан верно, в случае, если по нему возможно сформулировать условие задачи принципиально правильно. При задач по кинематике на рисунке должны быть указаны начальная и конечная точки нахождения тела (и намерено оговоренные промежуточные положения), указаны собственными обозначениями все расстояния, скорости, ускорения (направление перемещения, начальные и конечные условия) и пр. Построение рисунка начинается при чтении условия задачи, дополняется при анализе условия задачи, и может корректироваться на протяжении всего последующего ответа (к примеру, вводятся недостающие размеры и изображаются).
Метод ответа задач по кинематике:
1. Выделить тело, перемещение которого рассматривается в задаче.
2. Узнать как движется это тело (вид перемещения)? Пояснить ответ (сообщено ли об этом прямо в условии задачи либо же имеется косвенные указания, тогда какие конкретно?)
3. Записать закон перемещения тела – неспециализированное равенство (формула зависимости), но с учетом условия задачи (начальная скорость: имеется либо же она равна нулю?, с какого именно момента ведется отсчет времени?, принципиально важно ли положение тела либо же – речь заходит лишь о пройденном расстоянии? и т.п.).
4. Взять на его базе конкретные равенства, высказывающие связь между данными и искомыми размерами.
5. Выразить из них искомую величину (либо величины), т.е. взять ответ задачи в общем виде.
6. Сделать диагностику размерности (устно либо письменно, в зависимости от сложности взятой формулы).
7. Произвести вычисления и проанализировать полученные числовые значения.
Замечания. Метод ответа конкретных физических задач в общем случае не может быть линейным, т.е. содержать однозначную последовательность действий, приводящих к их ответу. Любой раз нужно учитывать конкретные изюминки, отражающиеся не только на виде конкретных равенств, но и последовательности их записи, методе выражения из них искомых размеров и т.д. Не обращая внимания на это, напомним, что число разных вариаций само собой разумеется и ими возможно овладеть полностью в ходе ответа большого, но ограниченного числа физических задач! Предложенный автором метод отражает самые важные, нужные (но время от времени не достаточные) компоненты ответа кинематических задач.
Примеры ответа задач
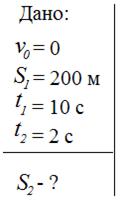 Задача-пример 1. Тело, выведенное из состояния спокойствия, двигаясь равноускоренно, прошло 200 м за 10 с. Какое расстояние прошло тело за 2 с от начала перемещения?
Задача-пример 1. Тело, выведенное из состояния спокойствия, двигаясь равноускоренно, прошло 200 м за 10 с. Какое расстояние прошло тело за 2 с от начала перемещения?
 Ответ: Нужно разглядеть пара состояний, каковые условимся именовать: начальное, 1-е и 2-е. В каждом из них перемещение характеризуется значением скорости, пройденным от начала перемещения расстоянием за соответствующий временной отрезок.
Ответ: Нужно разглядеть пара состояний, каковые условимся именовать: начальное, 1-е и 2-е. В каждом из них перемещение характеризуется значением скорости, пройденным от начала перемещения расстоянием за соответствующий временной отрезок.
По условию перемещение есть равноускоренным. Так как о положении тела по отношению к вторым телам ничего не говорится, то записываем закон равноускоренного перемещения для пройденного пути (форма 1, см. ф-лу (2)):
тогда 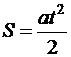 . Для участков 0-1 и 0-2 приобретаем соответственно конкретные равенства:
. Для участков 0-1 и 0-2 приобретаем соответственно конкретные равенства: 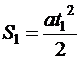 и
и 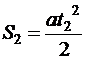 . Делим одно на второе и высказываем искомое расстояние:
. Делим одно на второе и высказываем искомое расстояние:
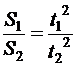 ?
? 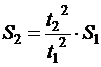 . Вычисляем:
. Вычисляем: 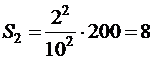 (м).
(м).
Ответ: за 2 с от начала перемещения тело пройдет 8 м. ¨
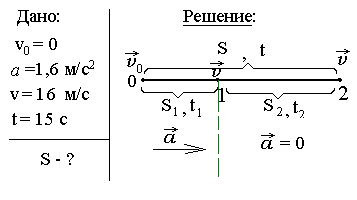 Задача-пример 2. Автомобиль остановился у светофора. По окончании того, как загорелся зеленый сигнал, он начинает двигаться с ускорением 1,6 м/с2 и движется так , пока скорость не станет равна 57, 6 км/ч, по окончании чего он продолжает перемещение с постоянной скоростью. На каком расстоянии от светофора автомобиль окажется спустя 5 с (10 с и 15 с) по окончании появления зеленого сигнала?
Задача-пример 2. Автомобиль остановился у светофора. По окончании того, как загорелся зеленый сигнал, он начинает двигаться с ускорением 1,6 м/с2 и движется так , пока скорость не станет равна 57, 6 км/ч, по окончании чего он продолжает перемещение с постоянной скоростью. На каком расстоянии от светофора автомобиль окажется спустя 5 с (10 с и 15 с) по окончании появления зеленого сигнала?
В первую очередь нужно ответить на вопрос: Как движется тело? Ответ «равноускоренно» – неверен! В условии четко сообщено, что тело движется равноускоренно только до определенного момента, что нужно непременно учесть, соответственно и продемонстрировать на рисунке – до положения 1 тело движется равноускоренно, после этого равномерно с заданной скоростью. Так, темперамент перемещения зависит от величины заданного промежутка времени!
Итак, пройденное расстояние складывается из пути при пути и равноускоренном движении при равномерном перемещении: S = S1+S2, где 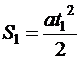 и . Тут — время равноускоренного перемещения от начальной нулевой скорости до известной конечной скорости, равной . Отыщем его из зависимости скорости от времени при равноускоренном перемещении (см. ф-лу (4)): ?
и . Тут — время равноускоренного перемещения от начальной нулевой скорости до известной конечной скорости, равной . Отыщем его из зависимости скорости от времени при равноускоренном перемещении (см. ф-лу (4)): ? 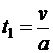 . Тогда
. Тогда 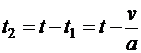 и . Находим искомое расстояние, подставляя отысканные выражения:
и . Находим искомое расстояние, подставляя отысканные выражения: 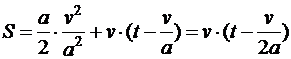 .
.
Мы взяли, помой-му, неспециализированное ответ. Решим задачу с учетом конкретных данных. Вычислим время, нужное с целью достижения заданной скорости при перемещении с данным ускорением : 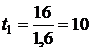 (с). Тогда делаем вывод, что при, в то время, когда t = 5 с, все 5 с тело будет двигаться равноускоренно и приобретаем:
(с). Тогда делаем вывод, что при, в то время, когда t = 5 с, все 5 с тело будет двигаться равноускоренно и приобретаем: 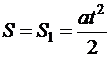 . Вычисляем:
. Вычисляем: 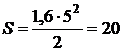 (м). В случае, если же t = 15 с, то используем взятую неспециализированную формулу полностью и приобретаем значение:
(м). В случае, если же t = 15 с, то используем взятую неспециализированную формулу полностью и приобретаем значение: 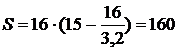 (м). Наряду с этим
(м). Наряду с этим 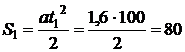 (м) и (м). Помимо этого, в случае, если задано t = 10 с, то возможно воспользоваться как формулой для S1, так и неспециализированной формулой для S:
(м) и (м). Помимо этого, в случае, если задано t = 10 с, то возможно воспользоваться как формулой для S1, так и неспециализированной формулой для S: 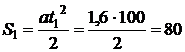 (м) либо
(м) либо 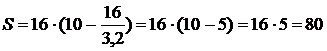 (м).
(м).
Итак, неспециализированное ответ задачи должно верно давать ответы для всевозможных числовых значений заданных в условии размеров! Тогда с учетом этого отечественное неспециализированное ответ будет иметь таковой вид:
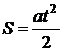 при
при 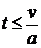 и
и 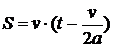 при
при 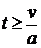 .
.
Ответ: спустя 5 с по окончании появления зеленого сигнала автомобиль окажется на расстоянии 20 м от светофора; через 10 с он будет на расстоянии 80 м, а через 15 с – на расстоянии 160 м от него. ¨
Замечание. Принципиально важно подчернуть, что полученная неспециализированная формула есть формулой зависимости пути от времени, т.е. законом перемещения автомобиля по окончании включения зеленого сигнала светофора, записанным в форме, высказываемой формулой (2). Т.е. приведенная как пример задача относится к группе задач, решаемых на базе записи закона перемещения тела в форме «зависимости пути от времени» (форма 1). Вторая несколько задач по кинематике предполагает запись закона перемещения выбранного тела в форме 2 – «зависимости координаты от времени» (см. формулу (3)).
Задача-пример 3. Тело кинуто с высоты H0 = 20 м вертикально вверх со скоростью V0 = 5 м/с. Где будет пребывать тело через время t = 0,5; 1; 2; 10 с? Отыскать время полета тела.
Разбирая условие задачи, убеждаемся в том, что в этом случае имеет значение положение тела (требуется ответить на вопрос «Где?»), т.е. его координата (перемещение одномерное – вд 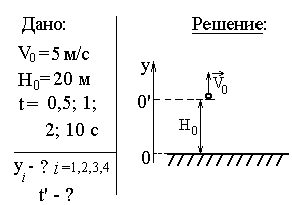 оль одной прямой, значит достаточно одной координаты, дабы совершенно верно задать положение тела), задающая положение тела по вертикали. Из этого делаем вывод о необходимости задания оси координат (направленной прямой с масштабом и началом отсчёта). Ось выбирается на протяжении направления перемещения, ее направление возможно выбрать двояко (вверх либо вниз), а начало отсчета возможно брать в любой точке. Данный момент в ответе задачи содержит некий «произвол» решающего. Выбор направления оси скажется на символе перед векторными размерами в записи закона перемещения (лишь и всего!), а положение начала отсчета должно будет учитываться при определении начальной координаты тела и при задании его положения соответствующими координатами. Второй момент требует рационального выбора начала отсчета с учетом условия задачи.
оль одной прямой, значит достаточно одной координаты, дабы совершенно верно задать положение тела), задающая положение тела по вертикали. Из этого делаем вывод о необходимости задания оси координат (направленной прямой с масштабом и началом отсчёта). Ось выбирается на протяжении направления перемещения, ее направление возможно выбрать двояко (вверх либо вниз), а начало отсчета возможно брать в любой точке. Данный момент в ответе задачи содержит некий «произвол» решающего. Выбор направления оси скажется на символе перед векторными размерами в записи закона перемещения (лишь и всего!), а положение начала отсчета должно будет учитываться при определении начальной координаты тела и при задании его положения соответствующими координатами. Второй момент требует рационального выбора начала отсчета с учетом условия задачи.
В нашем случае в задаче известна высота, с которой кинуто тело, соответственно хотелось бы ответить на поставленный вопрос указанием соответствующего расстояния от поверхности Почвы до искомого положения тела. Исходя из этого выбираем начало отсчета так, дабы высота тела над почвой была равна его координате, т.е. у поверхности Почвы.
Ясно, что закон перемещения сейчас нужно записывать в форме 2. Определим сперва вид перемещения. Неверно заявить, что тело движется «равнозамедленно» (так только на участке перемещения вверх) либо «равноускоренно» (так только на участке перемещения вниз). Верно будет заявить, что тело движется с постоянным ускорением под действием силы тяжести, т.е. = = const. Приобретаем:
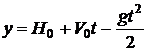 — это неспециализированная формула зависимости от . Подставляя вместо одной из этих переменных некое ее значение (к примеру, t1), машинально вместо второй переменной делается соответствующее значение (y1) и напротив. Это крайне важное для понимания событие ложится в базу получения конкретных равенств.
— это неспециализированная формула зависимости от . Подставляя вместо одной из этих переменных некое ее значение (к примеру, t1), машинально вместо второй переменной делается соответствующее значение (y1) и напротив. Это крайне важное для понимания событие ложится в базу получения конкретных равенств.
Итак, при t = t1 y = y1, т.е. подставляем и приобретаем:
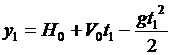 , подобно для всех данных в условии значений времени. Но!!! Учитывая физическую сущность задачи (в отличие от математических абстракций, выраженных формулами), нужно подметить, что координата тела разна только в то время, когда тело движется (изменяет положение в пространстве). В противном случае говоря, в случае, если тело перестает двигаться, то для всех последующих значений времени ее координата остается неизменной! В нашем случае, в то время, когда тело упадет на Землю, его координата станет равной нулю и будет такой для всех значений времени , где t’ – время полета тела (время его перемещения над поверхностью Почвы). Его значение ищем подстановкой:
, подобно для всех данных в условии значений времени. Но!!! Учитывая физическую сущность задачи (в отличие от математических абстракций, выраженных формулами), нужно подметить, что координата тела разна только в то время, когда тело движется (изменяет положение в пространстве). В противном случае говоря, в случае, если тело перестает двигаться, то для всех последующих значений времени ее координата остается неизменной! В нашем случае, в то время, когда тело упадет на Землю, его координата станет равной нулю и будет такой для всех значений времени , где t’ – время полета тела (время его перемещения над поверхностью Почвы). Его значение ищем подстановкой:
при t = t’ y =0, т.е.
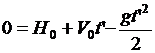 . Решаем это квадратное уравнение, приведя предварительно его к виду приведенного квадратного уравнения:
. Решаем это квадратное уравнение, приведя предварительно его к виду приведенного квадратного уравнения:
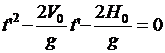 ,
,
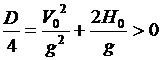 , значит математически имеется два корня:
, значит математически имеется два корня:
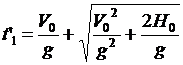 и
и 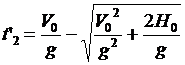 .
.
Разумеется, что второй корень при любых значениях начальной скорости будет отрицательным, соответственно задача имеет только единственное физическое ответ:
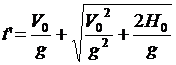 .
.
Вычисляем 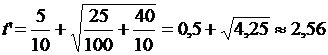 (с) – искомое время полета тела. Сейчас возможно сообщить, чему равна координата тела, к примеру, при t4 = 10 с: y4 = 0.
(с) – искомое время полета тела. Сейчас возможно сообщить, чему равна координата тела, к примеру, при t4 = 10 с: y4 = 0.
Неспециализированное ответ данной задачи получается поэтому в виде:
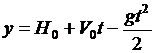 при
при 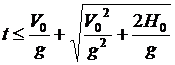 и
и
при 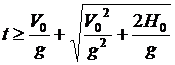 .
.
Вычисляем искомые значения координат:
y(0,5) = 20 + 5?0,5 — 5?0,25 = 21,5 (м) – выше начального положения,
y(1) = 20 + 5?1 — 5?1 = 20 (м) – на той же высоте, что и в начале,
y(2) = 20 + 5?2 — 5?4 = 10 (м) – ниже начального положения,
y(10) = 0 (м) – на поверхности почвы. ¨
Задача-пример 4. На горизонтальном валу, совершающем 200 об/с, на расстоянии 20 см друг от друга закреплены два узких диска. Для определения скорости полета пули произведен выстрел так, что пуля пробила оба диска на однообразном расстоянии от оси вращения. Выяснить скорость пули, в случае, если угловое смещение пробоин выяснилось равным 180.
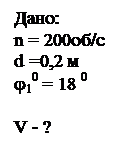 Ответ: В данной задаче рассматриваются различные тела с разными видами перемещения.
Ответ: В данной задаче рассматриваются различные тела с разными видами перемещения.
Так, разглядывая вращательное перемещение пробоин, возьмём закон вращения: , где . Подставим: — неспециализированная формула зависимости угла поворота пробоин за время t.
Иначе, разглядывая равномерное перемещение пули, возьмём для нее закон перемещения: — неспециализированная формула зависимости пройденного расстояния от времени перемещения пули (форма 1).
На базе взятых неспециализированных формул запишем сейчас конкретные равенства с учетом данных задачи. Для этого обозначим через t1 – время полета пули между двумя дисками. Тогда за время t1 пуля пройдет расстояние d, а вторая пробоина повернется на угол , т.е.:
и .
Делим второе на первое и высказываем искомую величину скорости пули:
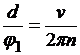 ?
? 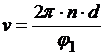 . Итак, получено ответ в общем виде. Но…! Обращаем внимание на требование соблюдение единой размерности однородных размеров. В дано записано значение угла поворота в градусах, тогда как все готовые формулы, каковые мы применяли при ответе предполагают, что угловые размеры измеряются в радианах! Исходя из этого нужно в неспециализированную формулу ответа включить параметры перевода градусов в радианы. Несложнее всего осуществлять переход по пропорции:
. Итак, получено ответ в общем виде. Но…! Обращаем внимание на требование соблюдение единой размерности однородных размеров. В дано записано значение угла поворота в градусах, тогда как все готовые формулы, каковые мы применяли при ответе предполагают, что угловые размеры измеряются в радианах! Исходя из этого нужно в неспециализированную формулу ответа включить параметры перевода градусов в радианы. Несложнее всего осуществлять переход по пропорции:
радиан — 3600
радиан — 0. Из этого 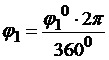 , тогда приобретаем:
, тогда приобретаем:
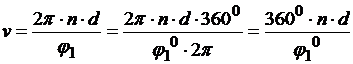 , т.е. совсем имеем:
, т.е. совсем имеем:
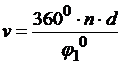 .
.
Вычислим:
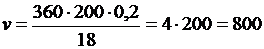 (м/с).
(м/с).
Ответ: скорость пули равна 800 м/с ¨
Задача-пример 5. Вслед движущемуся со скоростью 7 м/с грузовику кинули мяч со скоростью 15 м/с. С какой скоростью мяч отлетит от кузова грузовика, в случае, если удар вычислять полностью упругим.
 Ответ: Делаем рисунок (рис. а), на котором показываем направления скоростей тел, разглядываемых в данной задаче.
Ответ: Делаем рисунок (рис. а), на котором показываем направления скоростей тел, разглядываемых в данной задаче.
Разбирая условие задачи, подмечаем, что мяч (Т) движется довольно двух совокупностей отсчета: почва (К) и грузовик (К’), причем V1 – переносная скорость ( ), а V2 – безотносительная скорость мяча ( — довольно К, т.е. Почвы). Причем спрашивается в задаче снова же про скорость относительно земли, тогда как сам удар происходит в совокупности отсчета К’.
Исходя из этого все ответ представим в три этапа:
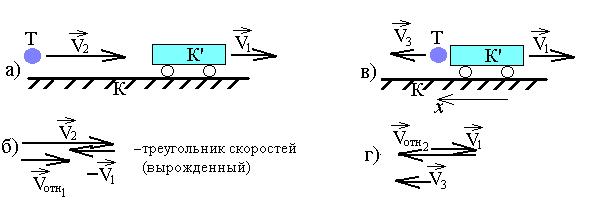 |
1 этап. Переходим к новой совокупности отсчета К’, т.е. отыщем из формулы сложения скоростей (15) относительную скорость мяча:
либо, в отечественных обозначениях: .Потом строим на базе векторного равенства треугольник скоростей (рис. б), из которого находим необходимое числовое значение: Vотн2 = V2 – V1 = 15 – 7 = 8 (м/с). С таковой скоростью мяч подлетает к грузовику. Это промежуточное вычисление возможно не делать.
2 этап. Разглядывая полностью упругий удар мяча о грузовик заключаем, что мяч отлетит от кузова со скоростью, равной по величине и противоположной по направлению по отношению к : .
Причем все это в совокупности К’.
3 этап. Переходим обратно в совокупность отсчета К. Полагая, что величина скорости грузовика не изменяется в следствии удара, делаем новый рисунок с указанием скоростей тел уже по окончании удара (рис. в). Используем снова формулу (15): .Строим по ней треугольник скоростей (рис. г) и приобретаем совсем значение искомой величины:
.
Как видим, формула неспециализированного ответа имеет векторный вид. Для нахождения числового значения искомой размеры выбираем на рисунке направление оси х и проектируем последнее равенство на нее: V3x = 2(-V1) – (-V2) = V2 – 2V1. Вычисляем: V3x = 15 — 2?7 = 1 (м/с).
Замечание. При, в то время, когда V2 2V1, мяч по окончании удара о кузов будет двигаться в прошлом направлении (т.е. вслед грузовику), но с меньшей скоростью.
Ответ: 1 м/с. ¨
ЗАДАЧИ к разделу «Кинематика»
Прямолинейное перемещение
1. За 4 с перемещения тело прошло путь 40 м. Какой путь тело пройдет за 8 с от начала отсчета времени, в случае, если начальная скорость равна 5 м/с. [120 м]
2. Тело, выведенное из состояния спокойствия, двигаясь равноускоренно, прошло 200 м за 10 с. Какое расстояние прошло тело за 2 с от начала перемещения?
3. Материальная точка движется с ускорением а. Выяснить разность дорог, проходимых точкой в два последовательных однообразных промежутка времени Dt.
4. При равноускоренном перемещении точка проходит в первые два равных промежутка времени по t = 4 с любой пути S1 = 24 м и S2 =64 м. Выяснить ускорение и начальную скорость.
5. Тело переместилось из точки А(-1;2) в точку В(5;3). Сделайте чертеж, отыщите его проекции и перемещение тела на оси координат.
6. Как мы знаем, что траектории двух материальных точек пересекаются. Столкнутся ли эти точки? Каково условие столкновения (встречи) двух точек?
7. Перемещение грузовика описывается уравнением х=-270+12t. Обрисуйте темперамент перемещения автомобиля. Отыщите начальную координату, направление и модуль вектора скорости, перемещение и координату автомобиля за 20 с. В то время, когда автомобиль пройдет через начало координат? Выстройте график зависимости х(t) и vx(t).
8. Перемещение двух велосипедистов описывается уравнениями х1=12t и х2=120-10t. Обрисуйте темперамент перемещения каждого велосипедиста, отыщите направление и модуль их скоростей, выстройте графики перемещения, графики скорости, и выясните графически и аналитически место и время встречи этих велосипедистов.
9. За одно и также время 2 автомобиля прошли однообразный путь. Первый автомобиль двигался с ускорением а с нулевой начальной скоростью. Второй – первую половину пути двигался со скоростью v1, а вторую половину – со скоростью v2. Отыскать путь, пройденный каждым автомобилем.
10. Двигаясь равноускоренно, велосипедист за время t1 увеличил собственную скорость от значения v1 до v2. После этого в течение времени t2 он двигался равномерно. Отыскать путь, пройденный велосипедистом за все время перемещения.
11. *Автобус движется в течение 20 с по прямой до остановки, проходя наряду с этим расстояние 310 м. Его начальная скорость 15 м/с. Докажите, что ускорение автобуса изменяется по направлению.
12. Два автомобиля выходят из одного пункта в одном направлении. Второй автомобиль выходит на 0,5 мин позднее первого. Оба движутся с однообразным ускорением 0,4 м/с2. Через какое количество времени, считая от начала перемещения первого автомобиля, расстояние между ними окажется 540 м?
13. Тело, имея начальную скорость V0 = 1 м/с, двигалось равноускоренно и купило, пройдя некое расстояние, скорость V = 7 м/с. Отыскать скорость на половине этого расстояния. [5 м/с]
14. Автомобиль начинает двигаться и первую часть пути проходит равноускоренно за время t1, а вторую равнозамедленно до полной остановки. Целый путь длиной l автомобиль проходит за время t. Выяснить его ускорение а1 на первой части пути.
15. На пути 60 м скорость тела уменьшилась втрое за 20 с. Выяснить скорость тела в конце пути, считая ускорение постоянным. [1,5 м/с]
16. Скорость тела на пути 106,25 м возросла на 5 м/с. Выяснить ускорение тела, в случае, если скорость в начале пути равна 6 м/с. [0,4 м/с2]
17. *В момент, в то время, когда опоздавший пассажир вбежал на платформу, мимо него прошел за время t1 предпоследний вагон. Последний вагон прошел мимо пассажира за время t2. На какое количество опоздал пассажир к поезду (t0)? Поезд движется равноускоренно. Протяженность вагонов однообразна.
18. *По наклонной доске разрешили войти катиться снизу вверх шарик. На расстоянии l = 30 см от начала пути шарик побывал два раза: через t1 = 1 с и через t2 = 2 с по окончании начала перемещения. Выяснить ускорение движения и начальную скорость шарика, считая его постоянным.