По итогам наблюдений выстроить графики нагрузка – перемещения с равномерной оцифровкой осей и в одном масштабе по оси перемещений. Указать все экспериментальные точки и совершить усредняющие прямые линии. В случае, если усреднённая линия (прерывистая на иллюстрации представления графиков) не проходит через начало координат, совершить соответствующую линию параллельную усредненной. В работе применять линии, проходящие через начало координат.
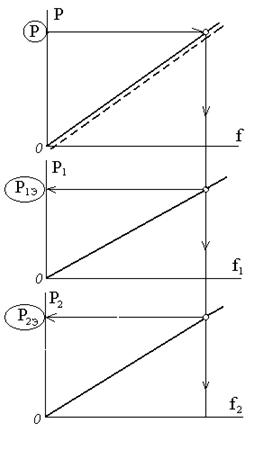Сравнение теоретического и экспериментального ответов
Указать нагрузку на совокупность Р (назначить произвольно) и по графикам найти значения и .
Выяснить и для принятого значения нагрузки Р по итогам теоретического ответа (см. теория).
Установить погрешности:
,
,
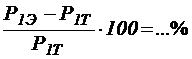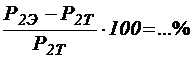Сравнить соотношения:
, 
.
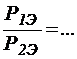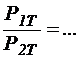Примечание: Модули упругости материала балок и возможно выяснить по соответствующим графикам (см. Опробование на изгиб).
Выводы. Заключение о итогах проверки с анализом вероятных источников погрешностей в опыте.
Лабораторная работа № 8
ИЗУЧЕНИЕ КОСОГО ИЗГИБА
Цель: экспериментальная проверка главных положений теории косого изгиба: определение положения нейтральной линии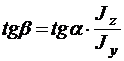 
и перемещений 
.
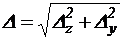III. Теория.
Под косым изгибом понимается таковой вид изгиба, в то время, когда плоскость действия изгибающего момента не сходится с главными центральными осями поперечного сечения стержня y, z(рис.1,а).
Косой изгиб появляется, к примеру, в случае, если перпендикулярная к оси стержня нагрузка действует в различных плоскостях (рис.1b), либо ориентирована произвольно по отношению к главным центральным осям (рис.1,с).
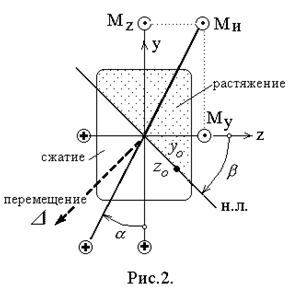На плоскости возможно применять следующее изображение моментов перпендикулярных к ней (рис.2). Косой изгиб представляется, как совокупность двух плоских изгибов в основных плоскостях моментами и . Результирующий момент определяется геометрической суммой:
,
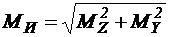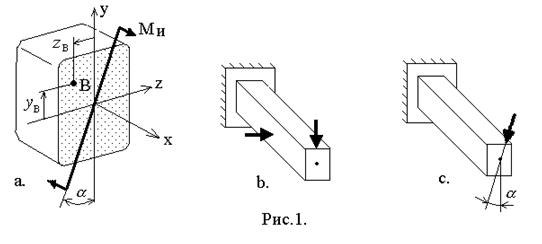
а угол наклона, в случае, если его отсчитывать от оси у, отношением:
.
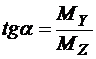Оси направляться направлять так, дабы результирующий момент проходил через I и III квадранты.
Обычные напряжения в любой точке сечения определяются алгебраической суммой напряжений от двух моментов:
.
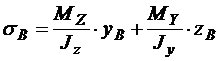Координаты точки имеют символы. Так, на рис.1,а координата отрицательна, хороша. Следовательно, во всех точках I квадранта напряжения хороши, а в точках III квадранта отрицательны. Нейтральная линия проходит через II и IV квадранты, и координаты её точек находятся из условия отсутствия напряжений в них:
.
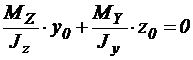Нейтральная линия проходит через центр тяжести сечения, и её положение возможно выяснить углом наклона к оси z:
.
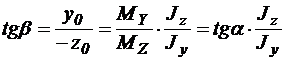В случае, если , то нейтральная линия в сечении стержня не перпендикулярна плоскости действия результирующего изгибающего момента ( ), стержень предпочитает изгибаться не в его плоскости, как это не редкость при плоском изгибе. Конкретно этим и обусловлено наименование косой изгиб. Для сечений с равными моментами инерции нейтральная линия перпендикулярна плоскости действия косого изгиба и результирующего момента нет.
Линейные перемещения сечений определяются геометрической суммой перемещений по направлениям основных осей.
II. Опыт
4. Установка для опробований стержня на изгиб.
5. Индикаторы часового типа (0,01мм).
6. Штангенциркуль, линейка.
 |
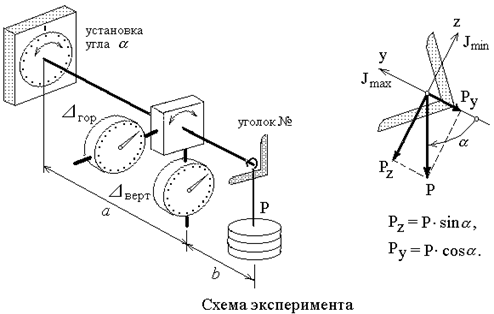На установке консольный стержень (равнобокий уголок) возможно установить под любым углом к вертикальной нагрузке, создаваемой гирями весом 1кг. Индикаторы показывают горизонтальное и вертикальное перемещения сечения в месте их размещения. Перед началом опыта установить размеры, номер уголка стержня и по сортаменту проката моменты инерции относительно главных центральных осей.
Изобразить заданную ориентацию уголка (н/п, как на схеме).
Опыт содержится в определении перемещений при трёх ориентациях стержня к нагрузке.
Таблица наблюдений
Обработка результатов экспериментов
 |
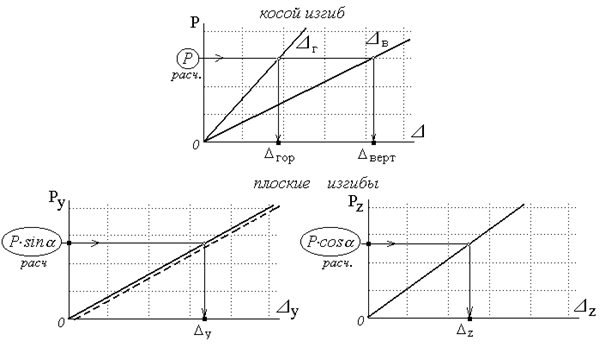По итогам наблюдений выстроить графики нагрузка – перемещения с равномерной оцифровкой осей. Указать все экспериментальные точки и совершить усредняющие прямые линии. В случае, если усреднённая линия (прерывистая на иллюстрации представления графиков) не проходит через начало координат, совершить соответствующую линию параллельную усредненной. В работе применять линии, проходящие через начало координат.
Сравнение опыта с теорией.
1. Положение нейтральной линии.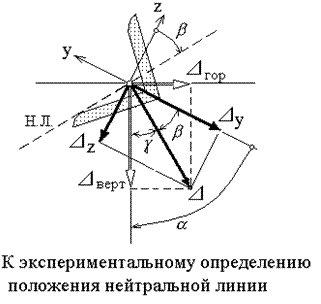 
(изобразить рис. для заданного угла ).
Для любого принятого (расчётного) значения нагрузки по графикам для косого изгиба находим перемещения в горизонтальном и вертикальном направлениях
, .
Из рисунка
, 
.
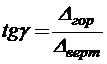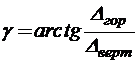Вычисляем угол: .
Его теоретическое значение:
.
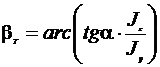Погрешность: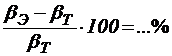 
.
2. Определение перемещений:
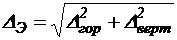= мм.
В теоретическом представлении косого изгиба двумя плоскими, разлагаем нагрузку на составляющие и из соответствующих графиков плоского изгиба определяем перемещения в направлениях основных осей
,
Полное перемещение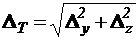 
= … мм.
Погрешность: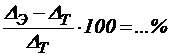 
 |
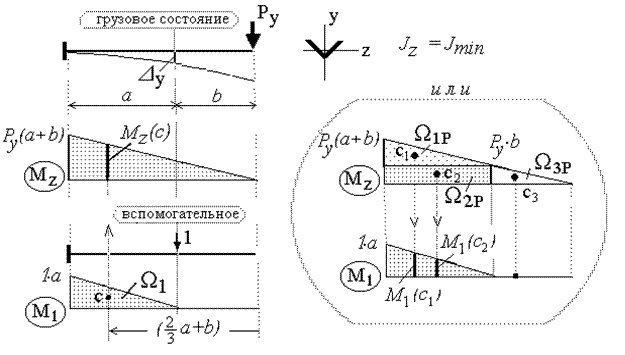Примечание 1: В представлении косого изгиба двумя плоскими изгибами теоретическое значение полного перемещения определяется кроме этого посредством универсального уравнения упругой кривой либо интегралов Мора, вычисляемых по методу Верещагина. Так, по методу Верещагина:
,
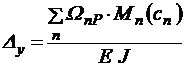где n число элементарных площадей диаграммы.
В случае, если диаграмма грузового состояния ограничена прямыми линиями (линейные функции) возможно перемножать площади диаграммы запасного состояния на ординаты диаграммы грузового состояния:
.
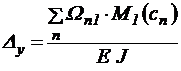Соответственно,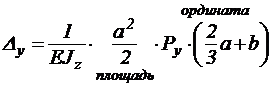 
.
Подобно для другого направления:
.
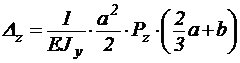Как возможно подметить (см. либо), перемножение площадей грузовой диаграммы моментов на ординаты запасном требует повышения вычислительной работы.
Примечание 2.Результаты измерений перемещений при изгибе стержня в направлениях основных осей разрешают по аналитическим связям перемещений с нагрузкой выяснить осевые моменты инерции сечения стержня, и сравнить их со значениями из сортамента металлического проката:
.
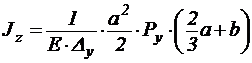Подобно определяется и .
Выводы. Заключение о итогах проверки с анализом вероятных источников погрешностей в опыте.
Лабораторная работа № 9
ОПРОБОВАНИЕ МАТЕРИАЛОВ НА УДАР
Цель: выяснить ударную вязкость материалов.
IV. Теория.
Опробования материалов медлительно изменяющейся нагрузкой (статической) не характеризуют абсолютно их механические особенности. В настоящих условиях эксплуатации многие элементы конструкции подвергаются скоро изменяющимся нагрузкам (динамическим) и, выбирая материал для них, нужно это учитывать.
При громадной скорости трансформации нагрузки развитие и образование пластических деформаций запаздывает, в следствии чего возрастает предел текучести и разрушающее напряжение (рис.1). Самый заметно влияние скорости деформирования при больших температурах.
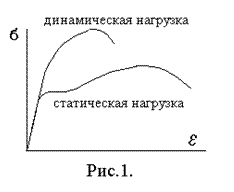В сопротивлении материалов конструкций упругому деформированию динамическая нагрузка представляется как статическая умноженная на коэффициент динамичности:
.
Соответственно этому представлению определяются напряжения, перемещения и формулируются жёсткости и условия прочности:
,
.
Ясно, что такое представление есть условным и приблизительным, и особенно, в определении величины допускаемых напряжений, каковые назначаются в большинстве случаев по итогам статических опробований.
Все жёсткие материалы, в какой то мере способны поглощать энергию удара. За эту меру принята условная величина, названная ударной вязкостью. Ударная вязкость определяется величиной работы, затраченной на разрушения примера особой формы, отнесённая к площади поперечного сечения в месте излома:
.
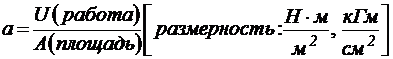В размерности ударной вязкости не допускаются сокращения.
Ударная вязкость не находит применения в расчётах на прочность. Эта особая черта употребляется для оценки свойства материалов сопротивляться ударным действиям. Для удовлетворительной работы в таких условиях её значение должно быть не меньше .
Ударная вязкость сталей зависит от их структуры и эту зависимость нельзя обнаружить при статических опробованиях.
 |
В таблице приведены результаты определения ударной вязкости мелкозернистой и крупнозернистой стали. Они проявляют практически однообразные прочностные и деформационные особенности в статических опробованиях, но существенно отличаются по ударной вязкости.
С понижением температуры ударная вязкость материалов понижается и существует температура критическая, при которой происходит резкое уменьшение её, и материал делается негодным для работы при динамических действиях. Изменение ударной вязкости отмечается и при повышенных температурах. Так, для углеродистых сталей она существенно понижается в промежутке температур .
II. Опыт
7. Машина для опробований на удар (маятниковый копёр).
8. Штангенциркуль.
 |
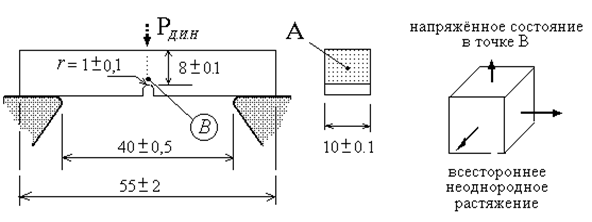схема и Образец опробования
Пример помещают вольно на плоские опоры так, дабы надрез был обращён в сторону противоположную удару по его направлению, и разрушают его одним ударом. Надрез находится в области растяжения. Форма надреза, размеры примера, скорость удара влияют на значение ударной вязкости. Расстояние между опорами (пролёт) не воздействует на результаты, в случае, если его отношение к высоте примера находится в пределах от 4 до 8.
Для получения сопоставимых результатов размеры и форма образцов стандартизируются. Надрез есть концентратором напряжений и помогает для сосредоточения (локализации) энергии удара в месте разрушения. Чем острее и глубже надрез, тем меньше делается область распространения пластической деформации. Материал в области надреза находится в условиях всестороннего растяжения. В направлениях перпендикулярных растягивающим напряжениям от изгиба появляются растягивающие напряжения от стеснения поперечных деформаций. Всестороннее растяжение (кроме того неоднородное) есть очень твёрдым условием работы материала и разрешает кроме того в самом пластичном материале найти хрупкость.
Перед опробованием осуществляется проверка размеров примера.
 |
Примечание.
Получение излома надрезанного примера ударом есть средством изучения структуры материала в материаловедении. Как мы знаем, что вид поверхности разрушения растянутого примера уже есть полезным добавлением к цифровым данным о особенностях материала. В случае, если в статических опробованиях влияние разных факторов на структуру материала есть как бы замаскированным (до разрыва примера в нём происходит большая деформация), то по виду структуры излома надрезанного примера уничтоженного ударом обнаруживается кроме того не сильный изменение в термической обработке материала.
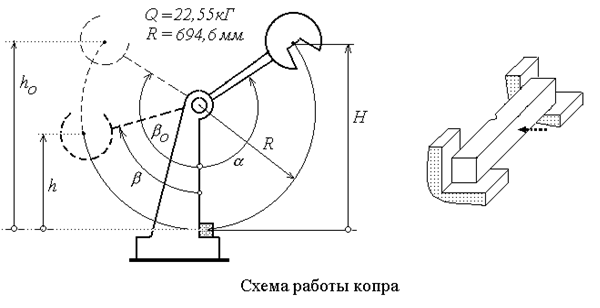
Вычисление работы затраченной на разрушение примера
Маятник поднимается в начальное положение на высоту Н, которая отмечается углом подъема . Из этого положения он освобождается и при отсутствии примера (холостой движение) в собственном перемещении, преодолевая сопротивление сил трения в опорном узле и воздуха, поднимается на высоту (угол ). Работа, затраченная на преодоление сил сопротивления на пути , определяется разностью потенциальных энергий маятника в крайних положениях:
.
С установленным примером энергия маятника расходуется на его преодоление и разрушение сил сопротивления на пути .
Полагая, что работа на преодоление сил сопротивления пропорциональна пройденному пути маятника, работа, затраченная на разрушение примера, находится из выражения:
.
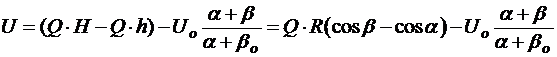Примечание: Перед тем как приступить к работе нужно ознакомится с устройством копра. При работе выполнять правила техники безопасности:
1. не находится в зоне перемещения маятника,
2. 
не останавливать маятник руками.
Таблица результатов и наблюдений
В таблице указать применяемую размерность размеров. Привести вычисление ударной вязкости и работ для каждого материала.
Выводы. сравнительное заключение и Характер разрушений о сопротивлении испытанных материалов удару.
Лабораторная работа № 10
ОПРОБОВАНИЕ НА УСТАЛОСТЬ (ВЫНОСЛИВОСТЬ)
Цель: изучение методики определения предела выносливости (усталости) материала.
V. Теория.
Усталостью материалов именуется явление их разрушения в следствии долгого действия переменных напряжений. Свойство материалов сопротивляться этому разрушению именуют выносливостью. Разрушение материалов от усталости происходит в механизмах и машинах с элементами во вращательном перемещении, возвратно-поступательном и сложных.
 |
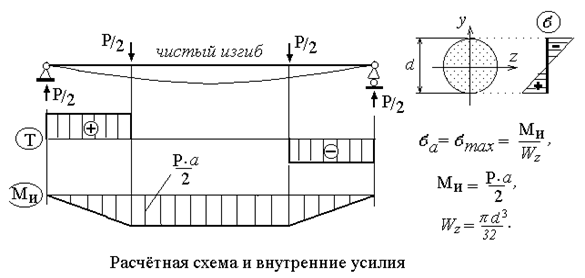
В несложных случаях перемещения элементов возможно установить закономерности в трансформации напряжений и обрисовать их аналитически (стационарный режим). В сложных перемещениях (к примеру, при перемещении автомобиля по грунтовой дороге) их возможно установить экспериментально в условиях эксплуатации автомобилей по записям характера перемещения, скоростей, ускорений (нестационарный режим либо хаотический).
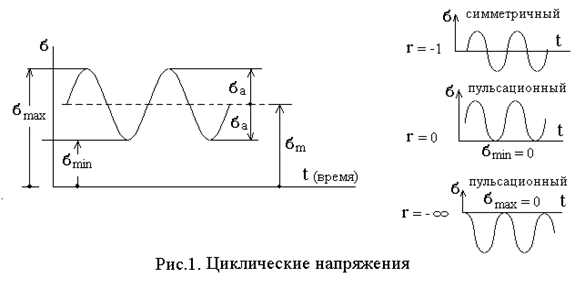
В стационарном режиме напряжения изменяются иногда (циклически). Под циклом принято осознавать совокупность последовательных значений напряжений за период (рис.1). Отношение минимального напряжения к его большому значению именуется коэффициентом асимметрии цикла:
.
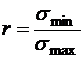Циклы с однообразным коэффициентом асимметрии именуют подобными.
Любой цикл возможно представлен как следствие наложения постоянного напряжения на напряжение, изменяющееся по симметричному циклу с амплитудой :
, 
.
 |
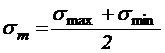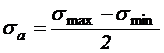Обстоятельством усталостного разрушения есть несовершенная упругость материалов. Прецизионные изучения явления упругого деформирования говорят о том, что линия разгрузки не сходится с линией нагрузки, образуя петлю гистерезиса (запаздывание следствия от создающей его обстоятельства).
Деформация материала связана с искажениями кристаллической решётки и трансформациями межатомного расстояния. Поликристаллическое строение материалов ведет к тому, что в зернах разным образом ориентированных к нагрузке появляются различные напряжения и в некоторых достаточные для образования микропластических деформаций. Это ведет к тому, что зерна, сохраняя по большей части связи и форму с соседними зернами, понемногу разрушаются микротрещинами, каковые в собственном развитии образуют магистральную. Поперечное сечение подробности ослабляется и происходит неожиданное разрушение. На поверхности излома обнаруживаются в большинстве случаев две территории: трещина на финальном этапе развития и свежая область хрупкого разрушения с выраженным кристаллическим строением. Образование микротрещин значительно чаще отмечается в зёрнах образующих поверхность. Тут при кручении и изгибе элементов появляются самые громадные напряжения.
Сопротивление материалов переменным напряжениям зависит лишь от и , каковые определяют петлю гистерезиса, и не зависит от характера трансформации напряжений в цикле (синусоидальное, пилообразное и др.).
В опробованиях на усталость пример либо конкретно подробность подвергают переменным напряжениям при растяжении, сжатии, изгибе, кручении либо их комбинации при воздействиях среды и различных температурах. Устанавливается число циклов, которое выдержал пример либо подробность до разрушения.
направляться различать сопротивление элементов конструкций и усталости материала из него. Элементы конструкций имеют различные размеры (масштабный фактор), концентраторы (отверстия, выточки, резкие трансформации поперечных сечений), разное уровень качества обработки (шлифование, точение), и любой из этих факторов воздействует на их усталостную прочность.
Полноценный теоретический анализ явления усталости в допущении представления материала как целой и однородной среды неосуществим. Содержание теории усталостной прочности на данный момент — это систематизация результатов экспериментов и разработка на их базе рекомендаций для практических расчётов.
Главная цель экспериментальных изучений — установление пределов выносливости для материала на особых примерах и на базе его учётом главных факторов, отличающих подробность от примера, определение предела выносливости для подробности.
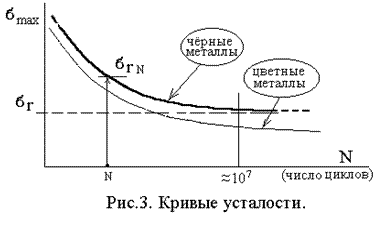
В случае, если представить графиком зависимость числа циклов до разрушения материала от величины заданных напряжений в нём, то она будет иметь очевидный темперамент: с уменьшением напряжений потребуется осуществить больше циклов до разрушения (рис.3.). С понижением уровня напряжений кривые становятся более пологими и асимптотически приближаются к некоему значению. В первый раз такие кривые взял Веллер и они именуются по его имени.
Для тёмных металлов (стали, чугуны) это асимптотическое рвение кривой более выражено, чем для цветных (медь, алюминий). Разумеется, под пределом выносливости (усталости) материала направляться осознавать громаднейшее напряжение в цикле (по модулю), которое определяет асимптоту (материал может трудиться без разрушения нескончаемое числе циклов). Число циклов, при котором фактически достигается асимптотическое значение, названо базисным. Для сталей за базу принимают 10 млн. циклов, для цветных металлов и для сталей высокой твёрдости в 5-10 раза больше, полагая, что в случае, если материал не разрушился, проработав это число циклов, то выдержит и большее. Опробования металлических образцов при обычной температуре подтверждают это представление. Соответственно, пределом выносливости именуется большое напряжение, при котором не происходит разрушения при осуществлении базисного числа циклов.
Предел выносливости имеет индекс, показывающий коэффициент асимметрии. Так, для симметричного цикла обозначение предела выносливости , для пульсационного .
Для расчёта подробностей, не предназначенных на долгий срок работы вводится понятие ограниченного предела выносливости , где N заданное число циклов (меньше базисного). Ограниченный предел выносливости устанавливается по кривой усталости.
 |
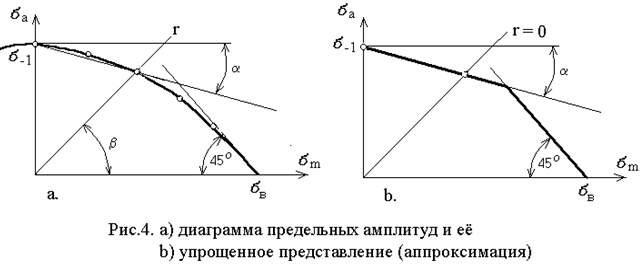Дабы абсолютно характеризовать сопротивление материала переменным напряжениям, нужно знать пределы выносливости при циклах с разной асимметрией. Совокупность их определяет диаграмму предельных напряжений (рис.4, диаграмма Хейя). На данной диаграмме в координатах прямая линия, совершённая под углом , определяет соответствующий цикл:
.
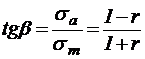Главная цель опробований на усталость – получение диаграммы предельных амплитуд, что есть долгим, сложным и трудоёмким мероприятием. Так, для её построения нужно иметь, как минимум, точек. Любая точка имеется итог построения кривой усталости Веллера, для получения которой нужно не меньше 10 точек. Выработка базисного числа циклов – это приблизительно 54 часа при 3000 оборотов в 60 секунд. Характерен громадный разброс экспериментальных точек и для точного определения предела выносливости требуется много образцов с последующей статистической обработкой результатов.
Упрощенную диаграмму предельных амплитуд определяют по пределам выносливости при симметричном и пульсационном циклах. Находят угловой коэффициент верхней прямой
: .
Правая часть диаграммы определяется прямой линией под углом из мысли, что большое напряжение цикла не имеет возможности быть больше предела прочности .
Систематизация многих опытов продемонстрировала, что величина коэффициента находится в диапазоне для углеродистых сталей и для легированных. При переменных касательных напряжениях величина коэффициента для этих же сталей и соответственно.
В учебном ходе достижимой целью лабораторной работы возможно лишь наблюдение процесса и изучение методики опробований на усталость.
II. Опыт
9. Машина для опробований (указать тип автомобили, число оборотов).
10. Штангенциркуль.
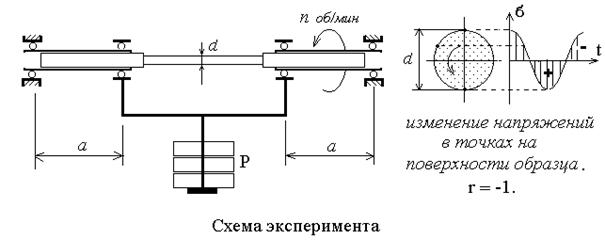
Пример: обычный обычный.
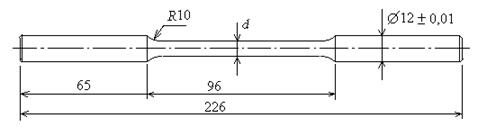
Для определения предела усталости (выносливости) материала поверхность рабочей части примера должна иметь высокий уровень качества обработки. Для качества влияния поверхности и исследования концентраторов рабочая часть примера должна иметь соответствующие недостатки. Влияние размеров (масштабный фактор) исследуется
 |
на примерах различного диаметра.
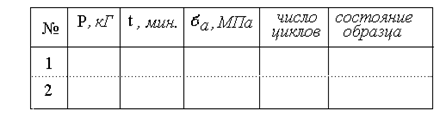
Таблица наблюдений: ,
В работе задаётся два уровня напряжений, состояние примера определяется по температуре нагрева.
 |
Наровне с классическим способом определения предела выносливости имеются предложения его ускоренного определения по измерению температуры примера, поглощению энергии, трансформациям электрических и магнитных особенностей. Незначительные трансформации этих параметров показывают на то, что напряжения не превышают предела выносливости.
Опробования на усталость в их современном состоянии требуют затраты громадного количества времени и потребность в разработке ускоренных новых способов делается всё более актуальной.
Выводы. Краткое изложение современных представлений об определении впечатления и предела выносливости от совершённого опыта.
Литература
1. Феодосьев В.И. Сопротивление материалов. — М.: Наука, 1979, 560 с.
2. Беляев Н.М. Сопротивление материалов. –М.: Наука, 1965.
3. Писаренко Г.С. и др. Сопротивление материалов. –Киев: Вища школа,1974, 672 с.