Неизвестные уравнения
Любая из рассмотренных задач сводится, как мы убедились, к ответу в целых числах некоего уравнения, содержащего более одного малоизвестного. Такие уравнения именуют неизвестными. При ответе неизвестных уравнений в большинстве случаев ищут значения малоизвестных, удовлетворяющие тем либо иным арифметическим условиям. К примеру, их решают в целых либо в рациональных числах.
Еще александрийский математик Диофант (III в. н. э.) занимался ответом алгебраических неизвестных уравнений в рациональных числах. Ответом неизвестных уравнений в целых числах в первый раз начали заниматься ученые Индии. Они внесли предложение неспециализированный способ для ответа в целых числах неизвестных уравнений первой степени с целыми коэффициентами, и нашли ответ в целых числах некоторых неизвестных уравнений второй степени с двумя малоизвестными.
Рациональные и целые ответа неизвестных уравнений первой степени. Способ рассеивания
Решить неизвестное уравнение первой степени с целыми коэффициентами в рациональных числах нетрудно. Заберём, к примеру, уравнение
Дабы отыскать все решения этого уравнения, определим, при каких рациональных значениях одного малоизвестного соответствующее значение второго малоизвестного рационально. Каждому значению малоизвестного x соответствует единственное значение малоизвестного у, определяемое из формулы:
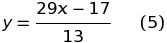
В случае, если значение малоизвестного x рационально, то и значение малоизвестного у, приобретаемое из формулы (5), рационально.
Для отыскания целых ответов уравнения (4) мы не можем конкретно воспользоваться формулой (5), так как при целых значениях одного малоизвестного второе малоизвестное не обязательно принимает целые значения. Дабы отыскать все целые ответа уравнения (4), будем искать такие значения малоизвестного ж, для которых соответствующее значение малоизвестного у есть целым числом. Это незначительное на первый взгляд изменение постановки задачи открывает путь для ее решения.
Подмечая, что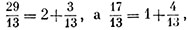 
мы пользуясь формулой (5), возьмём:
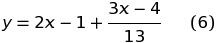
Будем решать задачу способом рассеивания.
Мы должны определить, при каких целых значениях малоизвестного ж малоизвестное у принимает целые значения. Так как при целом ж число 2x—1 есть целым, то из формулы (6) направляться, что малоизвестное у при целом x лишь в том случае принимает целое значение, в случае, если выражение (3x — 4)/13 имеется целое число. Отечественная задача еще не решена, но мы приблизились к цели.
В действительности, полагая
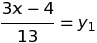
мы подмечаем, что вопрос, при каких целых значениях малоизвестного ж малоизвестное ух принимает целые значения, равносилен вопросу о целых ответах уравнения
Так, ответ в целых числах уравнения (4) нам удалось свести к ответу в целых числах уравнения (7). Чем же второе уравнение предпочтительнее первого?
Самым несложным из неизвестных уравнений конечно вычислять такое, у которого хотя бы один из коэффициентов при малоизвестных равен 1 либо —1. В этом случае малоизвестное с таким коэффициентом при любых целых значениях остальных малоизвестных принимает целые значения. Исходя из этого чем меньше мельчайшая из полных размеров коэффициентов при малоизвестных, тем уравнение предпочтительнее. В уравнении (4) мельчайшая из безотносительных размеров коэффициентов при малоизвестных равна 13, а в уравнении (7) эта величина равна 3. Как удалось достигнуть этого? Коэффициент при малоизвестном ж и вольный член уравнения были заменены остатком от деления этих чисел на 13. Но остаток от деления целого числа на натуральное число в любой момент меньше этого натурального числа. Ясно сейчас, по какой причине сначала малоизвестное у было выражено через малоизвестное х: мы выбрали малоизвестное с мельчайшим по полной величине коэффициентом. Мы купили некий опыт и можем сейчас смело приняться за уравнение (7).
При каких целых значениях малоизвестного y, малоизвестное х принимает целые значения?
Из равенства
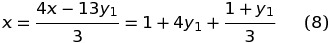
находим, что малоизвестное х при целых значениях малоизвестного y, лишь в том случае принимает целые значения, в случае, если (1+y1)/3 имеется целое число. Обозначая через x1, это выражение, возьмём: 1 + y1 = 3×1 либо
Так, задача сведена к ответу в целых числах уравнения (9). Но решить в целых числах уравнение (9) — значит определить, при каких целых значениях малоизвестного x1, малоизвестное y1, кроме этого принимает целые значения. Но y1 = 3×1 — 1, исходя из этого y1, принимает целые значения при любых целых значениях малоизвестного x1,. Сейчас из равенств (8) и (6) последовательно отыщем выражения для малоизвестных x и y:
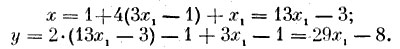
Из приведенных рассуждений направляться, что
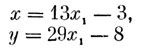
при x1 = 0, ±1, ±2, ±3,… дают все целые ответа уравнения (4).
Совершенно верно так же возможно поступить и в том случае, в то время, когда число малоизвестных в неизвестном уравнении первой степени больше двух. Для этого необходимо выбрать малоизвестное с мельчайшим (по полной величине) коэффициентом и поставить вопрос, при каких целых значениях вторых малоизвестных выбранное малоизвестное принимает целые значения. Легко додуматься, как поступать дальше. Обрисованный способ ответа неизвестных уравнений в целых числах несущественно отличается от способа, предложенного индийцами. В связи с тем, что при ответе неизвестного уравнения по этому способу оно сводится к цепочке уравнений с уменьшающимися коэффициентами, индийские математики назвали данный способ способом рассеивания.