Наибольшее и наименьшее значения функции.

Кафедра гуманитарных и естественнонаучных дисциплин

А.Б. ДЮБУА, С.Н. МАШНИНА

Матанализ: изучение

Функций одной переменной

Допущено учебно-методическим советом Рязанского филиала

национального образовательного учреждения высшего профобразования «Столичный национальный университет экономики, информатики и статистики (мэси)» в качестве учебного пособия для студентов Рязанского филиала МЭСИ, обучающихся по профессиям:

080801 – «Прикладная информатика (по областям)»; 080111 – «Маркетинг»; 080507 – «Менеджмент организаций»; 080503 – «Антикризисное управление»; 080109 – «Бухучёт, аудит и анализ»;080105 – «кредит и Финансы».

Протокол №3 от19 января.2011 г.

Рязань 2011

УДК 517.2

ББК 22.15

Д11

Критик:

каф. высшей математики Рязанского национального радиотехнического университета (зав. каф. К.В. Бухенский, к.ф.-м.н., доцент).

Дюбуа А.Б., Машнина С.Н. Матанализ: изучение функций посредством производных, – Рязань: Рязанский филиал МЭСИ, 2011 г. – 48 с.

Составлено в соответствии с Национальным образовательным стандартом по высшей математике для профессий: 080801 – «Прикладная информатика (по областям)»; 080111 – «Маркетинг»; 080507 – «Менеджмент организаций»; 080503 – «Антикризисное управление»; 080109 – «Бухучёт, аудит и анализ»; 080105 – «кредит и Финансы».

убывание и Возрастание функции.

Чтобы дифференцируемая на промежутке функция была возрастающей на этом промежутке, нужно и достаточно, дабы выполнялось условие

при всех .

Подобно, условие

при всех

есть нужным и достаточным для убывания дифференцируемой на промежутке функции .

Примеры

1.1.Доказать, что функция строго возрастает на промежутке .

n Так как

,

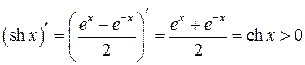то для всех функция есть строго возрастающей на всей области определения.?

1.2.Доказать, что в случае, если 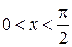, то .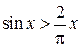

n Пускай 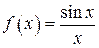, тогда . Эта функция дифференцируема на промежутке 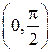, причем

,

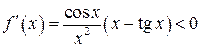то для всех 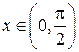функция строго убывает на промежутке 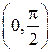. Исходя из этого

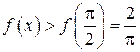
для всех .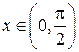

Другими словами выполнено

.?

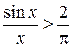
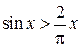Экстремумы функции.

Нужное условие экстремума.

Точки экстремума функции направляться искать среди тех точек области определения, в которых производная данной функции или равна нулю, или не существует. Точки, в которых производная данной функции равна нулю, именует стационарными точками данной функции, а точки, в которых функция постоянна, а её производная или равна нулю или не существует,— ее критическими точками.

Достаточные условие экстремума.

1) В случае, если меняет символ с минуса на плюс при переходе через точку , то — точка строгого минимума функции . В случае, если меняет символ с плюса на минус при переходе через точку , то — точка строгого максимума функции .

2) Пускай и существует вторая производная . Тогда, в случае, если , то — точка строгого минимума функции . В случае, если , то — точка строгого максимума функции .

Примеры

2.1. Отыскать точки экстремума функции

.

n Функция дифференцируема на множестве всех настоящих чисел, исходя из этого все её точки экстремума находятся среди стационарных точек функции, являющихся корнями уравнения , т.е. уравнения

,

которое имеет корни , 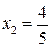, . Для удобства составим таблицу:

		возрастает
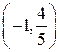
		возрастает
		max
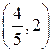
		убывает
		min
		возрастает

Из таблицы видно, что 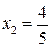, — точки минимума и строгого максимума, а не есть точкой экстремума. ?

2.2.Отыскать точки экстремума функции

.

n В первую очередь, напомним, что функция — четная, постоянная на , дифференцируемая на , не считая точек . Эквивалентное представление функции:

.

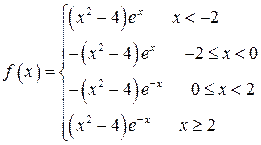Производная функции равна

,

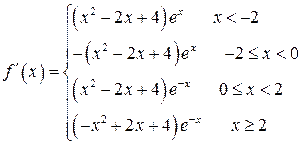критическими точками которой будут , , .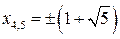

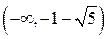
Составим таблицу

		возрастает
		max
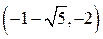
		убывает
	не существует	min
		убывает
	не существует	max
		убывает
	не существует	min
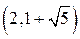
		возрастает
		max
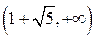
		убывает

Применяя полученные результаты, приобретаем: и — точки строгого минимума функции , 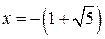, и — точки строгого максимума данной функции.?

Громаднейшее и мельчайшее значения функции.

Пускай функция постоянна на отрезке и имеет максимумы в точках , ,…., и минимумы в точках , ,…, и не имеет вторых точек экстремума. Тогда громаднейшее значение функции на отрезке равняется солиднейшему из чисел , , ,…., , , а мельчайшее данной функции на отрезке равняется мельчайшему из чисел , , ,…., , .

Примеры

3.1.Отыскать громаднейшее и мельчайшее значение функции

на отрезке .

n Как направляться из примера 2.1.функция на отрезке имеет строгий максимум в точке 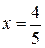и строгий минимум в точке . Следовательно, громаднейшее значение функции на отрезке равняется

,

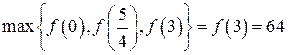а мельчайшее

.?

3.2.Отыскать громаднейшее и мельчайшее значение функции

на отрезке .

n Как направляться из примера 2.2.функция на отрезке имеет строгий максимум в точках и и строгий минимум в точке . Следовательно, громаднейшее значение функции на отрезке равняется

,

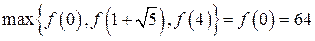а мельчайшее

.?

3.3.Корабль стоит на якоре в 10 км от ближайшей точки берега, матросу нужно добраться до лагеря расположенного в 15 км на протяжении берега. В каком точке берега обязан пристать матрос, дабы попасть в лагерь в скором будущем? Скорость матроса на веслах 4 км/час, пешком 5 км/час.

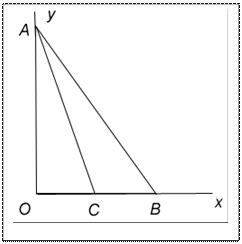n Свяжем условие задачи с декартовой совокупностью координат. Пускай корабль находится в точке , лагерь в точке , точка — место высадки матроса. Тогда суммарное время, нужное матросу, чтобы добраться из в будет равняется .

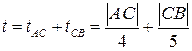Так задача сводится к нахождению минимума функции

.

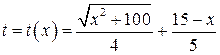Находя производную, приобретаем

.

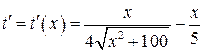Решая уравнение , находим стационарную точку 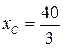. Следовательно, мельчайшее значение функции на отрезке равняется

.?

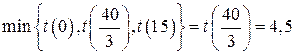3.4.Из сектора радиуса свертывается конус. При каком центральном угле он имеет громаднейший количество?

n Количество конуса вычисляется по формуле 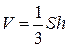, где — площадь круга — основания конуса, — его высота. Пускай — протяженность окружности основания конуса, разумеется, она равна длине дуги исходного сектора, т.е. и 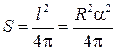. Высота взятого конуса равна

,

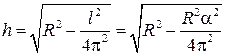а его количество, как функция угла

.

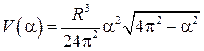Отыщем стационарные точки функции . Находя производную

,

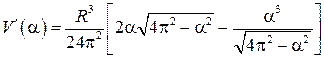и решая уравнение , приобретаем 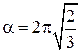. Нетрудно убедиться, что при данном значении угла, количество конуса будет большим.?

3.5.Отыскать положительное число, сумма которого и обратного к нему есть мельчайшей.

n Обозначим искомое число через . Исследуем функцию

.

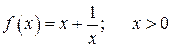Вычислим производную: .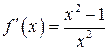

Производная имеет суть для всех , не считая . Критические точки функции: Так как число хорошее, имеем только одну точку для ответа: . Определим значение функции для . Слева от точки производная отрицательная, справа – хорошая. Значит, точка — точка минимума.

Используем второе достаточное условие экстремума. Для этого отыщем вторую производную:

.

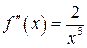Определим значение второй производной в критической точке : . Следовательно, это значение мельчайшее. Исходя из этого: . ?

3.6.Во дворе детского садика нужно огородить прямоугольной формы цветник, прилегающий к забору, протяженность которого больше 40 метров. Имеется 200 плит, любая из которых имеет длину 40 см. Каким должны быть размеры цветника, дабы его площадь была громаднейшей?

n Пускай — протяженность одной стороны цветника, параллельной забору, — протяженность смежной стороны цветника. Тогда: . По условию задачи протяженность изгороди: м. Следовательно,

;

;

;

.

Отыщем критические точки функции .

;

.

Отыщем громаднейшее значение функции на отрезке .

;

;

.

Взяли, что громаднейшее значение функции при .

Так, цветник будет иметь громаднейшую площадь, в случае, если сторона, прилегающая к забору, в два раза больше второй.

Отыщем вторую производную:

.

Так как вторая производная отрицательная, значит, — точка максимума.?

3.7.Из пункта А в направлении к пункту В отправляется грузовик со скоростью км/ч. В один момент из пункта В со скоростью 60км/ч отправляется автобус в направлении, перпендикулярном АВ. В какой момент времени от начала перемещения расстояние между автомобилями будет громаднейшим,

n В момент времени t расстояние между автомобилями равняется ЕС.

– расстояние, которое прошла грузовая машина. Тогда:

.

— прямоугольный. Используя теорему Пифагора, имеем:

.

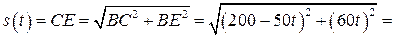
Так как автомобили двигались не меньше 4 часов , то искать мельчайшее значение функции будем на отрезке .

Отыщем производную

.

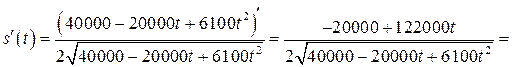
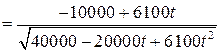Отыщем критические точки функции:

; ; ч.

60 секунд.

Определим значения функции в критических точках:

.

;

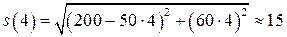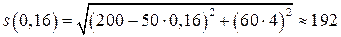в момент времени часа. ?

3.8.На малом предприятии создают продукцию одного вида. Затраты на производство единицы (в у. е. ) выражаются формулой:

.

Доход, полученный от её реализации:

.

Выясните, какое количество продукции нужно произвести, дабы прибыль от её реализации была большой?

n Прибыль от реализации товара определяется разностью между затратами и доходом:

.

Для отечественной задачи:

.

Для нахождения точки максимума функции применим нужное условие существования экстремума функции:

либо .

Последнее условие имеет экономический суть: чтобы прибыль была большой, нужно, дабы предельный доход .

;

;

;

;

.

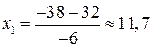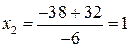Находим:

— громаднейшая прибыль.

Значит, нужно произвести 11,7 единиц продукции.

Наибольшее значение функции на отрезке (а,b) — bezbotvy

Интересные записи:

• На тему: «история открытки»
• Настоящий момент есть все 3 глава
• Наибольшего по возрастанию
• На тему «правильное питание»