Начала статистической физики: макро- и микросостояния, статистический ансамбль
Состояние газа, характеризуемое его давлением, объёмом и температурой, именуется макроскопическим.
Состояние газа, характеризуемое скоростями и положениями всех его частиц, именуется микроскопическим. В случае, если число частиц n ( в 1см3 при н.у.) то микроскопическое состояние газа характеризуется 6п числами (микропараметрами): 3п координатами всех частиц и 3п проекциями их скоростей . Все эти числа направляться разглядывать как случайные размеры.
Сосуд с заключенными в нем частицами именуется статистической совокупностью.
Совокупность однообразных статистических совокупностей именуется статистическим ансамблем.
Микроканонический ансамбль складывается из однообразных изолированных совокупностей с однообразной энергией. Не считая микроканонических ансамблей в статистической физике рассматриваются кроме этого канонические и другие ансамбли.
Одно и также макроскопическое состояние осуществляется в солидном числе совокупностей ансамбля, находящихся в разных микроскопических состояниях. Следовательно, данное макросостояние характеризуется солидным числом микросостояний.
В состоянии ТД равновесия все микросостояния равновероятны. Это постулат равновероятности.
Начала статистической физики: эргодическая догадка, статистический вес, статистическое толкование энтропии
Эргодическая догадка говорит, что такая средняя скорость равняется средней скорости, вычисленной по ансамблю совокупностей, т.е. среднее значение величины, вычисленное по времени равняется среднему значению величины, вычисленному по ансамблю совокупностей.
Пускай число совокупностей в ансамбле , в некий момент времени :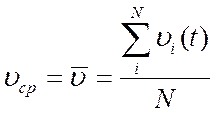 
Статистический вес Г: определяется числом микросостояний, реализующих данное макросостояние. Причем честен постулат равновероятности всех микросостояний.
Статистический вес Г еще именуют термодинамической возможностью состояния совокупности. Т.к. это число способов, которыми возможно реализовано данное макросостояние совокупности, по определению, . Так, термодинамическая возможность не есть возможность в математическом смысле (т.к. ).
Формула Больцмана разрешает дать энтропии следующее определение (статистическое толкование).
Энтропия есть мерой неупорядоченности совокупности. Энтропия имеется количественная мера беспорядка совокупности многих частиц.
В действительности, чем больше число микросостояний реализующих данное макросостояние, тем больше энтропия.
Начала статистической физики: флуктуации
величина флуктуирует, в случае, если ее значение колеблется около среднего. В термодинамике и статистической физике в большинстве случаев имеются в виду флуктуации внутренних параметров в состоянии термодинамического равновесия.
Мерой флуктуаций есть стандартное отклонение от среднего значения, которое выяснено равенством для дискретных размеров: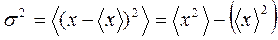 
Расчет относительной величины флуктуации посредством распределения Пуассона дает величину: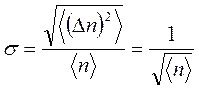 
.
Напомним, что относительная роль флуктуаций возрастает с уменьшением области, в которой эти флуктуации рассматриваются. В случае, если область пытается к величине количества совокупности, то число частиц в данной области пытается к числу частиц совокупности.
Так как флуктуации уменьшаются как , следовательно, с ростом числа частиц в макросистемах флуктуации становятся ничтожно малыми.
Исходя из этого поведение совокупности солидного числа частиц возможно обрисовывать посредством средних размеров, характеризующих совокупность.
Характерные скорости распределения Максвелла: средняя арифметическая скорость
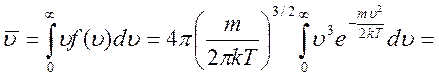выделим для замены переменной
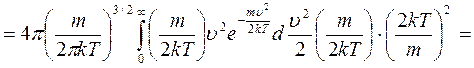
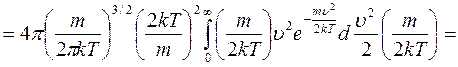сделаем замену переменной и учтем, значение табличного интеграла: 
, 
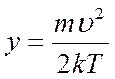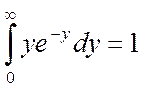, возьмём по окончании сокращения констант:
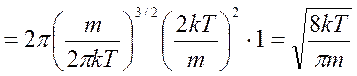, где — постоянная Больцмана, — масса молекулы, преобразуем, умножив знаменатель и числитель дроби на число Авогадро:
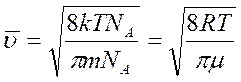, где — молярная масса компоненты совокупности.
Итог: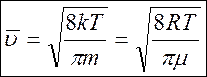 
— средняя арифметическая скорость перемещения молекул совершенного газа.
Распределение Больцмана
Плотность возможности того, что молекула имеет положение в промежутке
– функция распределения Больцмана
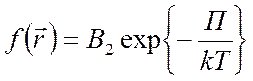
Возможность того, что частица находится в количестве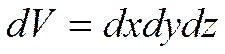 
, вблизи точки 
—
.
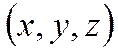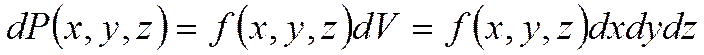Барометрическая формула
, 
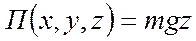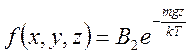, тогда число частиц в количестве ,
.
Масса частиц в количестве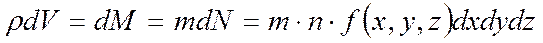 
, из этого
.
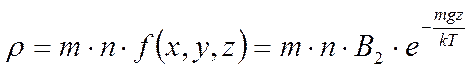Пускай , тогда обозначив, — плотность на уровне моря, а , возьмём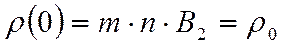 
связь между высоты и плотности 
.
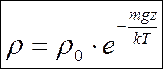В случае, если учтем уравнение состояния совершенного газа, то возьмём зависимость давления от
высоты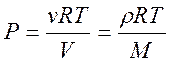 
возьмём ? 
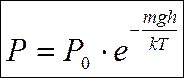— барометрическая формула.
Статистика Бозе-Эйнштейна
Подсчет числа состояний в распределении Бозе-Эйнштейна. В модели Бозе-Эйнштейна в каждом квантовом состоянии может пребывать произвольное число неразличимых между собой частиц. Как и при выводе распределения Ферми-Дирака, используем понятия энергетических возможных состояний и уровней в пределах отдельного уровня.
Наряду с этим условии неспециализированное число разных распределений частиц по местам выражается формулой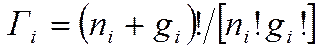 
. Тогда неспециализированное число микросостояний на всех энергетических уровнях:
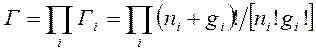— число микросостояний для модели Бозе-Эйнштейна.
Рассуждая равно как и при выводе распределения Ферми-Дирака возьмём формулу:
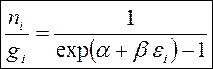— распределения Бозе-Эйнштейна.
Эта формула переходит в распределение Максвелла-Больцмана при, в то время, когда среднее число частиц, приходящихся на одно квантовое состояние, достаточно мало.
Протяженность свободного пробега
Молекулы газов сталкиваются между собой. Между двумя последовательными соударениями молекула проходит путь , что именуют длиной свободного пробега. Конечно, что суть имеет лишь средняя протяженность свободного пробега
, 
, ;
, ? 
, ? 
.
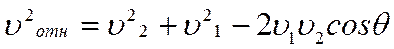
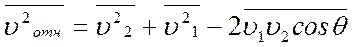
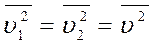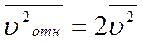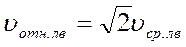Переход к относительной скорости, внесет в взятую формулу множитель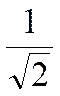 
:
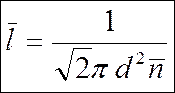— средняя протяженность свободного пробега.
Явление переноса: диффузия
Процесс переноса массы именуется диффузией
Разглядим сейчас две области с различной концентрацией одного и того же вещества либо различных веществ. Самопроизвольно появляются потоки молекул, сглаживающие концентрацию. Экспериментально установлен закон Фика:
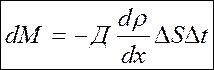, где — плотность (возможно закон написать через концентрацию),
— коэффициент диффузии, , символ “-“ показывает, что диффузия идет из области с большей концентрацией в сторону области с меньшей концентрацией.
Изотермы Вандер-Вальса
Для изучения поведения настоящего газа разглядим изотермы Ван-дер-Ваальса— кривые зависимости при заданных значениях , определяемые уравнением Ван-дер-Ваальса (2.2) для моля газа. Эти кривые (рассматриваются для четырех разных температур; рис. 89) имеют необычный темперамент. При больших температурах ( ) изотерма настоящего газа отличается от изотермы совершенного газа лишь некоторым искажением ее формы, оставаясь монотонно спадающей кривой. При некоей температуре на изотерме имеется точка перегиба . Эта изотерма именуется критической,соответствующая ей температура — критической температурой.Критическая изотерма имеет только одну точку перегиба — именуемую критической точкой;в данной точке касательная к изотерме параллельна оси абсцисс. Соответствующие данной точке давление и объём именуются кроме этого критическими.Состояние с критическими параметрами ( ,,) именуется критическим состоянием.При низких температурах( ) изотермы имеют волнообразный участок, сперва монотонно опускаясь вниз, после этого монотонно поднимаясь вверх и опять монотонно опускаясь.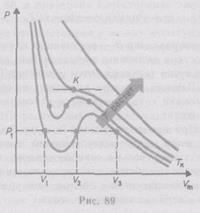 
Для пояснения характера изотерм преобразуем уравнение Ван-дер-Ваальса (3) к виду:
. (3.1)
В таком виде уравнение, при заданных и , есть уравнением третьей степени довольно .
Кубическое уравнение может иметь или три вещественных корня, или один вещественный и два мнимых.Причем физический суть имеют только вещественные хорошие корни. Исходя из этого первому случаю соответствуют изотермы при низких температурах (три значения количества газа , и отвечают одному значению давления ), второму случаю— изотермы при больших температурах.
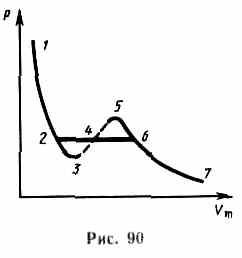Разглядывая разные участки изотермы при (рис.90), видим:
на участках 1—3 и 5—7 при уменьшении количества давление возрастает, что соответствует естественному поведению газа;
на участке 3—5 сжатие вещества ведет к уменьшению давления; опыт говорит, что такие состояния в природе не осуществляются. Наличие участка 3—5 свидетельствует, что при постепенном трансформации количества вещество не имеет возможности оставаться все время в виде однородной среды; в некий момент должно наступить распад вещества и скачкообразное изменение состояния на две фазы.
Так, подлинная изотерма будет иметь вид ломаной линии 7—6—2—1.
Часть 7—6— отвечает газообразному состоянию;
часть 2—1 — жидкому;
часть6—2,— горизонтальный участок, соответствующий равновесию жидкой и газообразной фаз вещества.
Вещество в газообразном состоянии при температуре ниже критической именуется паром,а пар, находящийся в равновесии со своей жидкостью, именуется насыщенным.
Эти выводы, следующие из анализа уравнения Ван-дер-Ваальса, были обоснованы опытами ирландского ученого Т. Эндрюса (1813—1885), изучавшего изотермическое сжатие углекислого газа. Отличие экспериментальных (Эндрюс) и теоретических (Ван-дер-Ваальс) изотерм содержится в том, что превращению газа в жидкость в первом случае соответствуют горизонтальные участки, а во втором — волнообразные.
Для нахождения критических параметров подставим их значения в уравнение (3.1) и запишем для одного моля:
(3.2)
Потому, что в критической точке все три корня совпадают и равны , уравнение приводится к виду
,либо . (3.3)
Так как уравнения (3.2) и (3.3) тождественны, то в них должны быть равны и коэффициенты при малоизвестных соответствующих степеней. Исходя из этого возможно записать:
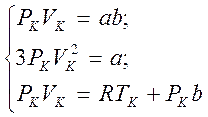Решая систему уравнений, отыщем:
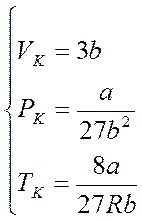. (4)
В случае, если решить совокупность довольно постоянных размеров , приобретаем:
.
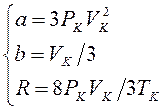Полученные соотношения говорят о том, что для каждого настоящего газа нужно вычислять его личную газовую постоянную , которая отличается от молярной газовой постоянной причем оказывается личная газовая постоянная меньше, чем молярная. Потому, что газовая постоянная пропорциональна числу молекул в моле, заключаем, что в критическом состоянии происходит уменьшение структурных единиц, образующих газовую постоянную, т.е. молекулы объединяются в комплексы. При удалении от критического состояния эти комплексы распадаются, и личная газовая постоянная делается равной молярной.
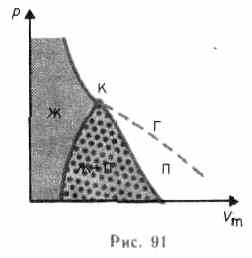В случае, если через крайние точки горизонтальных участков семейства изотерм совершить линию, то окажется колоколообразная кривая (рис. 91), ограничивающая область двухфазных состояний вещества. критическая изотерма и Эта кривая делятдиаграмму , под изотермой на три области: под колоколообразной кривой находится область двухфазных состояний (насыщенный пар и жидкость), слева от нее находится область жидкого состояния, а справа — область пара. Пар отличается от остальных газообразных состояний тем, что при изотермическом сжатии претерпевает процесс сжижения. Газ же при температуре выше критической не может быть перевоплощён в жидкость ни при каком давлении.
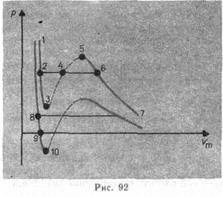Сравнивая изотерму Ван-дер-Ваальса с изотермой Эндрюса (верхняя кривая на рис. 92), видим, что последняя имеет прямолинейный участок 2—6, соответствующий двухфазным состояниям вещества. Действительно, при некоторых условиях смогут быть реализованы состояния, изображаемые участками ван-дер-ваальсовой изотермы 5—6 и 2—3. Эти неустойчивые состояния именуются метастабильными.
Участок 2—3 изображает перегретую жидкость,
5—6—пересыщенный пар.Обе фазы ограниченно устойчивы.
При низких температурах изотерма пересекает ось , переходя в область отрицательных давлений (нижняя кривая на рис. 92). Вещество под отрицательным давлением будет в состоянии растяжения. При некоторых условиях такие состояния кроме этого реализуются. Участок 8—9 на нижней изотерме соответствует перегретой жидкости,участок 9— 10 — растянутой жидкости.
Смачивание
Из практики как мы знаем, что капля воды растекается на стекле и принимает форму, изображенную на рис. 98, тогда как ртуть на той же поверхности преобразовывается в пара сплюснутую каплю (рис. 99). В первом случае говорят, что жидкость смачивает жёсткую поверхность, во втором — не смачивает ее. Смачивание зависит от характера сил, действующих между молекулами поверхностных слоев соприкасающихся сред. Для смачивающей жидкости силы притяжения между молекулами твёрдого тела и жидкости больше, чем между молекулами самой жидкости, и жидкость пытается расширить поверхность соприкосновения с жёстким телом. Для несмачивающей жидкости силы притяжения между молекулами твёрдого тела и жидкости меньше, чем между молекулами жидкости, и жидкость пытается уменьшить поверхность собственного соприкосновения с жёстким телом.
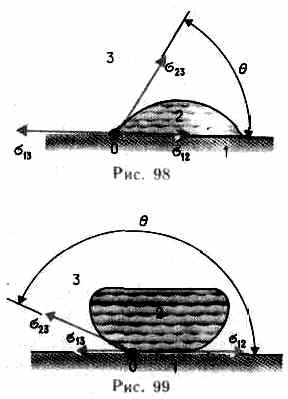К линии соприкосновения трех сред (точка О имеется ее пересечение с плоскостью чертежа) приложены три силы поверхностного натяжения, каковые направлены по касательной вовнутрь поверхности соприкосновения соответствующих двух сред (рис. 98 и 99). Эти силы, отнесенные к единице длины линии соприкосновения, равны соответствующим поверхностнымнатяжениям , , . Угол между касательными к поверхности твёрдого тела и жидкости именуется краевым углом. Условием равновесия капли (рис. 98) есть равенство нулю суммы проекций сил поверхностного натяжения на направление касательной к поверхности жёсткого тела, т. е.
,откуда
. (6.1)
Из условия (6.1) вытекает, что краевой угол возможно острым либо тупым в зависимости от значений и . В случае, если , то и угол — острый (рис. 98), т.е. жидкость смачивает жёсткую поверхность. В случае, если , то и угол — тупой (рис. 99), т. е. жидкость не смачивает жёсткую поверхность.
Краевой угол удовлетворяет условию (6.1), в случае, если . (6.2)
В случае, если условие (6.2) не выполняется, то капля жидкости 2 ни при каких значениях не имеет возможности пребывать в равновесии. В случае, если , то жидкость растекается по поверхности жёсткого тела, покрывая его узкой пленкой (к примеру, керосин на поверхности стекла),— имеет место полное смачивание (в этом случае ). В случае, если , то жидкость стягивается в шаровую каплю, в пределе имея с ней только одну точку соприкосновения (к примеру, капля воды на поверхности парафина),— имеет место полное несмачивание (в этом случае ).
Смачивание и несмачивание являются понятиями относительными, т. е. жидкость, смачивающая одну жёсткую поверхность, не смачивает другую. К примеру, вода смачивает стекло, но не смачивает парафин; ртуть не смачивает стекло, но смачивает чистые поверхности металлов.
Явления смачивания и несмачивания имеют громадное значение в технике. К примеру, в способе флотационного обогащения руды (отделение руды от безлюдной породы) ее, мелко раздробленную, взбалтывают в жидкости, смачивающей пустую породу и не смачивающей руду. Через эту смесь продувается воздушное пространство, а после этого она отстаивается. Наряду с этим намоченные жидкостью частицы породы опускаются на дно, а крупинки минералов «прилипают» к пузырькам воздуха и всплывают на поверхность жидкости. При механической обработке металлов их смачивают особыми жидкостями, что облегчает и активизирует обработку.
ЭФФЕКТ ДЖОУЛЯ-ТОМСОНА
Изменение температуры настоящего газа в следствии его адиабатического расширения, либо, как говорят, адиабатического дросселирования — медленного прохождения газа под действием перепада давления через дроссель (к примеру, пористую перегородку), именуется эффектом Джоуля — Томсона. Эффект Джоуля — Томсона принято именовать хорошим, в случае, если газ в ходе дросселирования охлаждается ( ), и отрицательным, в случае, если газ нагревается ).
В зависимости от условий дросселирования для одного и того же газа эффект Джоуля — Томсона возможно как хорошим, так и отрицательным. Температура, при которой (для данного давления) происходит изменение символа результата Джоуля — Томсона, именуется температурой инверсии.
Ее зависимость от количества возьмём, приравняв выражение к нулю:
Эффект Джоуля — Томсона обусловлен отклонением газа от идеальности, наличием сил сотрудничества. При дросселировании мы как бы разъединяем молекулы, и эта работа осуществляется за счет уменьшения либо повышения средней кинетической энергии молекул.
Температура
Температура – физическая величина, характеризующая состояние термодинамического равновесия макроскопической совокупности и определяющая направление теплообмена между телами.
На данный момент применяют 2 температурные шкалы:
Интернациональная практическая шкала (шкала Цельсия) калиброванная в градусах Цельсия по двум реперным точкам – температурам кипения и замерзания воды при давлении 1,013*10^5 Па, каковые принимаются соответсявенно 0 и 100.
Термодинамическая температурная шкала (шкала Кельвина) – калиброванная в градусах кельвина, определяется по одной реперной точке – тройной точке воды – температуре, при которой лёд, насыщенный пар и вода при давлении 609 Па находится в термодинамическом равновесии. Температура данной точки по данной шкале равна 273,16 К. Температура Т=0 именуется нулём Кельвина.
T=273.15+t
Начала статистической физики: макро- и микросостояния, статистический ансамбль
Состояние газа, характеризуемое его давлением, объёмом и температурой, именуется макроскопическим.
Состояние газа, характеризуемое скоростями и положениями всех его частиц, именуется микроскопическим. В случае, если число частиц n ( в 1см3 при н.у.) то микроскопическое состояние газа характеризуется 6п числами (микропараметрами): 3п координатами всех частиц и 3п проекциями их скоростей . Все эти числа направляться разглядывать как случайные размеры.
Сосуд с заключенными в нем частицами именуется статистической совокупностью.
Совокупность однообразных статистических совокупностей именуется статистическим ансамблем.
Микроканонический ансамбль складывается из однообразных изолированных совокупностей с однообразной энергией. Не считая микроканонических ансамблей в статистической физике рассматриваются кроме этого канонические и другие ансамбли.
Одно и также макроскопическое состояние осуществляется в солидном числе совокупностей ансамбля, находящихся в разных микроскопических состояниях. Следовательно, данное макросостояние характеризуется солидным числом микросостояний.
В состоянии ТД равновесия все микросостояния равновероятны. Это постулат равновероятности.