Билинейное преобразование – это способ преобразования частотной области передаточной функции аналогового фильтра в в цифровой фильтр Преобразование является следствием замены переменных
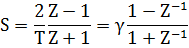
Оно именуется билинейным, в силу того, что и знаменатель и числитель данного преобразования являются линейными функциями от . Чтобы понять эффект преобразования, допустим, что – нормированная частота аналогового фильтра, а – нормированная частота цифрового фильтра. Частотная черта цифрового фильтра возможно взята из методом замены , а для аналогового фильтра путём замены в
Аналоговые и цифровые частоты соотносятся выражением
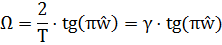
направляться иметь в виду, что частотная черта аналогового фильтра определяется на всей хорошей полуоси частот от до , тогда как у цифрового фильтра она имеет тот же суть лишь до частоты , т.е. до . Ясно, что шкала частот цифрового фильтра оказывается деформированной относительно шкалы частот аналогового фильтра. На рисунке 2.3 проиллюстрировано явление деформации АЧХ цифрового фильтра при билинейном преобразовании. Из рисунка видно, что на частоте АЧХ цифрового фильтра достигает того же значения, которое частотная черта аналогового фильтра имела бы на нескончаемой частоте.
Рисунок 3.3 – Деформация АЧХ фильтра при билинейном преобразовании:
а) АЧХ аналогового ФНЧ; б) АЧХ цифрового ФНЧ
На рисунке 2.4 изображена зависимость (2.3) и проиллюстрировано явление деформации частотной шкалы. Слева продемонстрирована идеализированная АЧХ аналогового полосового фильтра с двумя полосами пропускания, равными по величине, но противоположными в различных частотных диапазонах. Полученный ЦФ будет иметь кроме этого две полосы пропускания, но ширина последней в области верхних частот будет намного меньше ширины ПП в области нижних частот.
Из рисунка видно, что в области нижних частот, где функция мелка, частотные характеристики аналогового и цифрового фильтров практически совпадают. Потом по мере ускорения роста функция тангенса, частотная черта дискретного фильтра все посильнее сжимается по горизонтали (если сравнивать с аналоговым прототипом).
Рисунок 3.4 – Связь между аналоговыми и цифровыми частотами.
Выход, но, очень несложен. Деформация шкалы частот не ведет к нарушению избирательных особенностей при билинейном преобразовании (и это основное). А деформацию шкалы частот возможно скомпенсировать посредством предыскажений в аналоговом фильтре.
Компенсация результата деформации может осуществляться методом предварительного искажения шкалы частот аналогового фильтра противоположным образом, так, дабы по окончании применения билинейного Z-преобразования критические частоты были перемещены назад, к требуемым значениям.
Предыскажения, либо масштабирование шкалы аналоговой частоты осуществляется методом замены на новое значение. Продемонстрируем, как это сделать. Во многих справочниках по расчету аналоговых фильтров граничная частота полосы пропускания принимается равной
Дабы частоты (либо ) цифрового фильтра пересчитывалась в , коэффициент ? необходимо забрать равным
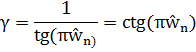
Подводя результат, необходимо отметить следующие характеристики билинейного преобразования:
- В случае, если аналоговый фильтр-прототип есть устойчивым, то результирующий цифровой фильтр кроме этого будет устойчивым;
- Порядок цифрового фильтра равен порядку аналогового прототипа;
- Частотная черта аналогового фильтра-прототипа сходится с частотной чёртом преобразованного цифрового фильтра, что свидетельствует: в случае, если аналоговый фильтр-прототип есть фильтром нижних частот, то и цифровой фильтр кроме этого будет фильтром нижних частот. Из этого второе наименование способа- способ инвариантности частотных черт;
- При билинейном преобразовании не сохраняются ни импульсная, ни фазо-частотная характеристики аналогового фильтра-прототипа.
Так, билинейное преобразование дает возможность приобрести передаточную функцию устойчивого цифрового фильтра, АЧХ которого удовлетворяет определенным требованиям избирательности.
Как находить общее сопротивление цепей. Преобразование треугольника в звезду
Интересные записи:
- Методологические аспекты рациональной организации труда руководителя (специалиста). другая заданная тема
- Мичилимакинак, остров большой черепахи, территория мичигана май 1814 года 14 глава
- Мичилимакинак, остров большой черепахи, территория мичигана май 1814 года 2 глава
- Мичилимакинак, остров большой черепахи, территория мичигана май 1814 года 3 глава