I. Подготовительный этап формирования способа (понятийный аппарат, основные действия и основные понятия) имеется в каждом из разглядываемых учебных пособий, не смотря на то, что он и не сосредоточен на каком-либо маленьком промежутке времени.
II. На мотивационном этапе возможно разглядеть с обучающимися ответ следующей задачи:
Задача. В трапеции ABCD углы А и В равны по 90°, а стороны АВ=2, ВС=1, AD=4.·Докажите, что диагонали данной трапеции взаимно перпендикулярны.
Задача решается несколькими методами и показывается, что векторный способ ответа задачи более несложен.
1 метод (рис. 24)
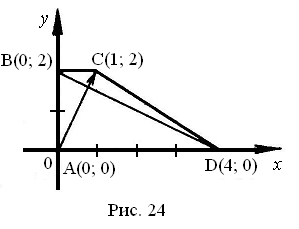
что и требовалось доказать.
Задание 4. Создайте другие методы ответа данной задачи, не связанные с применением векторного способа. Сравните эти методы ответа и оцените эффективность каждого.
Задание 5. Решите задачу: «Точки и являются соответственно точками пересечения медиан граней ABD и BCD тетраэдра ABCD. Доказать различными способами, что : а) векторным; б) координатным; в) классическим; г) геометрических преобразований. Какой из способов ответа данной задачи действеннее?
Задание 6.
III. На примере ответа первой задачи совершите ориентировочный этап, т.е. разъясните сущность способа и продемонстрируйте его главные компоненты:
1) Узнается, что необходимо доказать на геометрическом языке.
— Что для этого достаточно доказать на векторном языке?
— Какую операцию осуществили?
2) Имеется ли в условии задачи векторы и ?
— Как именно возможно взять векторы и ?
3) Записывается скалярное произведение векторов.
4) Выполняются преобразования и получается, что .
5) Переводится векторное равенство на геометрический язык.
Показывается, как возможно вырабатывать выделенные компоненты векторного способа.
Первое воздействие, которому нужно научить обучающихся, — это перевод геометрических соотношений на векторный язык. Для создания умения делать это воздействие целесообразно с обучающимися решать задачи типа
1. Точка А в собственности отрезку ВС. Запишите это соотношение в векторной форме.
2. Прочтите запись на геометрическом языке . (Точка М в собственности прямой АВ.)
3. Отрезки АВ и МК параллельны. Запишите это соотношение в векторной форме.
4. Точка С — середина отрезка АВ. Как это соотношение записать в векторной форме?
5. Прямые АС и МР параллельны. Как записать это соотношение в векторной форме? Имеется ли отличие в записи ответов задач 3 и 5? По какой причине?
6. Запишите в векторной форме условие перпендикулярности прямых АВ и РK.
Ответ этих и других аналогичных задач нужно оформить в виде таблицы в кабинете и первое время ею пользоваться при ответе задач векторным способом.
Обучающимся показывается самый целесообразный выбор совокупности координат (в том случае, в то время, когда это нужно) и выбор базовых векторов.
Это воздействие формируется у обучающихся посредством задач:
- Отыщите угол между векторами и .
- Четыре точки заданы собственными координатами: А (3; 1), В (1; 4), С (1; 0), D (4; 5). Выясните угол между прямым и АВ и CD.
Замечание. В задачах 1 и 2 совокупность координат выбирается произвольно, по окончании чего строятся точки по координатам и условие задачи записывается в векторной форме.
- В прямоугольной трапеции МРКС длины сторон МР=4, РК=2, МС=8.Докажите, что диагонали трапеции взаимно перпендикулярны. Не решая задачи, продемонстрируйте, какая совокупность координат самый целесообразна для поиска ответа данной задачи.
- Дана верная четырехугольная пирамида SABCD, в которой боковые ребра наклонены к плоскости основания под углом ?,точка К — середина ребра BS. Отыщите угол ? между прямыми АК и SC. Не решая задачу, укажите, какое размещение совокупности координат самый целесообразно для ее решения.
- К вершине куба приложены три силы в 1Н, 2Н, 3Н, направленные по диагоналям граней куба, проходящим через эту вершину. Отыщите величину равнодействующей этих трех сил.
Независимая работа
1. Проанализируйте пробные книжки по геометрии Л.С. Атанасяна и др. [45], [46], [47] и А.Д. Александрова и др. [17], [18], [19], [20], [16] и ответьте на вопросы:
1) Какова трактовка понятия «вектор», принятая каждым авторским коллективом?
2) Какие конкретно элементы векторного аппарата и в каких классах вводятся?
3) Разрешает ли совокупность задач организовать понятийный аппарат, отдельные компоненты векторного способа и векторный способ ответа задач в целом?
2. Пользуясь нижеуказанной литературой, подберите совокупности задач на формирование каждого компонента векторного способа.
Литература: [45], [65], [92], [113], [118], [129], [127].
Лабораторная работа № 18
Тема. Способ геометрических преобразований при изучении математики в школе.
Цели. Выделить характеристические показатели способа геометрических преобразований и разглядеть особенности его изучения по разным школьным книжкам математики.
Замысел
- Способ геометрических преобразований и его применение в школьном курсе математики.
- Геометрические преобразования как объект изучения в школе.
- Применение способа геометрических преобразований при изучении теоретического материала и ответе задач.
Главное содержание
Сущность любого математического способа, среди них и способа геометрических преобразований, пребывает в построении модели одной теории (в нашем случае классической евклидовой геометрии) в объектах второй (группы геометрических преобразований). Значительным показателем математической модели есть наличие изоморфизма между моделью и моделируемой теорией. Установим наличие указанного изоморфизма между множеством прямых и точек плоскости Евклида и множеством инволюционных элементов группы перемещений, т.е. множеством осевых и центральных симметрий. Каждой точке А ставится в соответствие центральная симметрия с центром в данной точке А,каждой прямой а — осевая симметрия с осью а.
Разные отношения между прямыми и точками плоскости Евклида смогут быть трактованы посредством композиций осевых и центральных симметрий. К примеру, отношение «точка А в собственности прямой а»соответствует тому, что композиции центральной симметрии относительно центра А и осевой с осью а,осевой относительно прямой а и центральной с центром А являются одно да и то же преобразование плоскости, т.е.
Наличие вышеуказанного изоморфизма и разрешает использовать способ геометрических преобразований при ответе задач, сформулированных в терминах евклидовой геометрии.
Способ геометрических преобразований в школе употребляется как средство обоснования некоторых взаимоотношений между элементами евклидовой геометрии (к примеру, конгруэнтности, параллельности и т.д.). Наряду с этим его использование в большинстве случаев предполагает исполнение следующей последовательности шагов:
— выбирается геометрическое преобразование, владеющее свойством, которое разрешает обосновать наличие указанного отношения между объектами евклидовой геометрии;
— выполняется преобразование, при котором один объект переходит в второй;
— обосновывается наличие указанного отношения между объектами посредством особенностей выбранного геометрического преобразования.
Выделенные шаги применения способа геометрических преобразований обусловливают необходимость актуализации главных понятий теории геометрических свойств и преобразований (неспециализированных и своеобразных) отдельных видов преобразований и овладение умением строить образы фигур при том либо другом преобразовании.
Продемонстрируем реализацию выделенной последовательности шагов при ответе следующей задачи способом геометрических преобразований:
3адача. На высоте BD треугольника АBC имеется точка К,такая, что АK=KC. Докажите, что треугольник АBC равнобедренный (рис. 25).
В задаче нужно установить конгруэнтность отрезков АB и BC(либо равенство их длин).
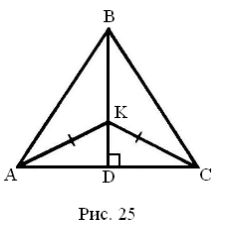Первый ход пребывает в выборе геометрического преобразования, которое владеет свойством сохранять расстояние. Именно это свойство разрешит обосновать отношение конгруэнтности между отрезками АВ и BC. В качестве для того чтобы преобразования целесообразно выбрать осевую симметрию относительно прямой BD.
Второй ход пребывает в том, дабы доказать, что при симметрии относительно прямой BD отрезок АВ перейдет в отрезок СВ. Это возможно доказать достаточно легко. Точка В перейдет сама в себя при выбранной симметрии, поскольку она есть точкой оси симметрии. Точка А перейдет в C при данной симметрии, поскольку эти точки на перпендикуляре к оси симметрии и АK=CK (К — точка оси симметрии).
Третий ход — последний этап ответа задачи. Так как отрезки АВ и СВ симметричны относительно оси BD, а симметрия есть перемещением (перемещением), то длины отрезков АВ и СВ (либо BC)равны.
К главным понятиям теории геометрических преобразований возможно отнести понятия отображения, преобразования, перемещения (перемещения), обратного преобразования, метода задания геометрического преобразования, конкретные виды геометрических преобразований.
К неспециализированным особенностям геометрических преобразований относятся следующие:
— композиция перемещений (перемещений) имеется перемещение (перемещение);
— преобразование, обратное перемещению (перемещению), имеется перемещение (перемещение);
— при перемещении (перемещении), и при преобразовании подобия прямые переходят в прямые, полупрямые — в полупрямые, отрезки — в отрезки; при указанных преобразованиях сохраняются углы между полупрямыми.
— при перемещении (перемещении) точки, лежащие на прямой, переходят в точки, лежащие на прямой, и сохраняется порядок их обоюдного размещения.
Выделяются своеобразные особенности каждого из конкретных видов геометрических преобразований (осевой и центральной симметрий, поворота, параллельного переноса, гомотетии, преобразования подобия), разглядываемых в школьном курсе математики.
Для каждого вида преобразования актуализируется метод построения образа фигуры при соответствующем преобразовании.
Геометрические преобразования в школе рассматриваются, во-первых, как объект изучения и, во-вторых, как главный инструмент способа.
В систематическом курсе геометрии изучаются преобразования фигур на плоскости и в пространстве. Наряду с этим преобразование фигуры понимается как ее смещение. Среди преобразований выделяются перемещения и преобразование подобия. Рассматриваются частные виды перемещении: осевая симметрия, центральная симметрия, поворот, параллельный перенос. Частным видом преобразования подобия есть гомотетия.
Выделим свойства и основные понятия, которые связаны с частными видами геометрических преобразований (на базе анализа книжки [113]).
Результатом данной работы возможно заполнение таблицы (табл. 15).
Таблица 15
| Наименование вида геометрического преобразования | Главные понятия, которые связаны с его изучением | Свойства геометрического преобразования |
| Центральная симметрия . . . | Центр симметрии. Центрально-симметричные фигуры (точки) относительно центра. Центрально-симметричная фигура | Преобразование симметрии относительно точки есть перемещением. (Все свойства перемещения применимы к центральной симметрии) |
Нужно обращать внимание на задание того либо иного вида преобразования, раздельно оговаривать комплект умений, каковые формируются у обучающихся при рассмотрении видов преобразований.
После этого нужно узнать, какие конкретно виды преобразований рассматриваются в пропедевтическом курсе геометрии (V — VI классы), умения и какие знания формируются при их рассмотрении.
Задание 1. Выполните анализ совокупности задач, помещенных по окончании пунктов «Ось симметрии» и «Центр симметрии» (см. [40]).
Итогом работы возможно заполнение таблицы (табл. 16).
Таблица 16
| Вид преобразования | Метод задания (на координатной плоскости, в пространстве) | Теоретический материал, при рассмотрении которого употребляются свойства прео6разования |
Задание 2. Выполните анализ ответа задачи, текст которой приведен в задании 3 для независимой работы.
Выделите этапы ответа данной задачи способом геометрических преобразований. Выделите умения, которыми должны овладеть обучающиеся, дабы применять способ при ответе данной задачи.
Создайте методику поиска ответа данной задачи.
Затем переходите к анализу совокупности задач, помещенных по окончании § 9 книжки [113]. Выделите задачи, направленные на усвоение знаний о геометрических преобразованиях; задачи, решаемые способом геометрических преобразований.
Выясните количественное соотношение этих задач и обоснуйте его.
Для получения нужных обобщений об изучении способа геометрических преобразований в школе выполните логико-дидактический анализ материала, связанного с геометрическими преобразованиями в неполной школе .
Независимая работа
1. Составьте перечень главных понятий, применяемых в теории геометрических преобразований, и фундаментальных особенностей отдельных геометрических преобразований, разглядываемых в школьном курсе математики.
2. Выделите понятия в пропедевтическом и систематическом направлениях геометрии, каковые вводятся посредством геометрических преобразований (см. [113]).
Выделите теоретический материал, при изучении которого употребляется способ геометрических преобразований.
3. Решите задачу, применяв способ геометрических преобразований, и выделите главные этапы ее решения.
Задача. Точка В лежит между точками А и С. По одну сторону от прямой АС выстроены равносторонние треугольники АЕВ и BFC. Доказать, что треугольник с вершинами в серединах отрезков AF и ЕС и точке В равносторонний.
4. Выполните логико-математический анализ теоретического материала § 9 из книжки [113].
5. Выполните анализ совокупности задач к § 9 книжки [113]. Выделите и решите задачи, в которых целесообразно применять способ геометрических преобразований.
Личные задания
1. Выделите типы задач, применяемые для создания понятия о геометрических преобразованиях фигуры: а) в книжке [23]; б) в книжке [24].
2. Установите изюминке изучения способа геометрических преобразований по книжке [45].
3. Приведите примеры применения способа геометрических преобразований при изучении курса алгебры.
Литература: [40], [45], [113], [125], [18].
Лабораторная работа № 19
Тема. Способы дифференциального исчисления в школьном курсе математики.
Цели. 1. Актуализировать знания о способе дифференциального исчисления.
2. Выяснить место, цели и значение изучения способа дифференциального исчисления в школе.
3. Продемонстрировать, что разглядываемый способ — наиболее значимый аппарат изучения естественных наук и математики.
4. Рассмотреть возможность применения способа при изучении математики.
5. Установить межпредметные связи.
Оборудование. Диафильмы «Постоянные функции», 07-3-446; «Предел функции. Производная», 07-3-139.
Главное содержание
I. С целью достижения поставленных целей нужно решить следующие методические задачи:
1. Установить содержание способа дифференциального исчисления.
2. Установить цели изучения этого способа в школьном курсе «начала и Алгебра анализа».
3. Выяснить умения и знания, которыми должны овладеть обучающиеся при изучении способа.
4. Уточнить уровень и содержание изложения соответствующего учебного материала, выделив «ядерный» и сопутствующий (неосновной) материал.
Одна из задач курса «начала и Алгебра анализа» содержится в завершении изучения функциональной линии курса алгебры неполной школы , где обучающиеся знакомятся с главными понятиями, результатами, способами матанализа в количестве, что разрешает изучить элементарные функции и решать несложные геометрические, физические и другие задачи.
Неспециализированная учебная задача, которая возможно поставлена при изучении элементов матанализа, — изучить способ, разрешающий использовать понятие производной к ответу разных учебно-практических задач.
Без понимания способа матанализа нереально разобраться в естественных науках, в технической и научно-популярной литературе. Это обусловлено тем, что математика попадает во все области деятельности человека.
Фундаментальным способом матанализа есть дифференциальное исчисление.
Главная мысль способа дифференциального исчисления пребывает в том, что, зная функцию и указав точку (либо не показывая ее), возможно дать локальную чёрта трансформации функции при трансформации довода.
Способ дифференциального исчисления выступает способом матанализа, поскольку с его помощью изучаются свойства разных классов функций. Помимо этого, производная выступает языком и инструментом, на котором описываются многие техники и процессы естествознания, исследуются и изучаются многие явления настоящего мира.
Математика используется в технике и естествознании для количественных характеристик и расчётов. Но взять расчетную формулу, к примеру, траектории ракеты либо прочности балки тяжело Тут и употребляется аппарат матанализа, что позволяет по изучению бесконечно малых элементов линий (поверхностей) — дифференциальное исчисление — в следствии взять требуемые формулы для объекта в целом — интегральные исчисления.
Обращение к вечно малым позволяет «кусок» кривой заменить отрезком (секущей либо касательной), установить какие-либо закономерности, применяя отрезки, несложнее, чем дуги кривых.
II. Узнав сущность способа дифференциального исчисления, нужно обратить внимание на образовательные, развивающие и воспитательные цели изучения разглядываемого способа:
— систематизировать знания о функциях, каковые имеются у обучающихся к началу изучения темы;
— ознакомить с новым способом изучения особенностей функции;
— продемонстрировать использование нового способа изучения особенностей функций к ответу разных прикладных задач;
— разъяснить обучающимся, что способ дифференциального исчисления — замечательнейший аппарат познания законов природы, и раскрыть роль этого аппарата для практики;
— распознать много возможностей более глубокого и всестороннего воспитания диалектико-материалистического мировоззрения.
Указанных целей возможно достигнуть по окончании независимого анализа соответствующих разделов программы по математике для средней общеобразовательной школы [119].
III. Анализ учебного пособия и программы по математике дает основание дать верные ответы на следующие вопросы:
Задание 1.
1) Каков понятийный аппарат способа дифференциального исчисления?
2) В чем специфика этого способа матанализа?
3) умения и Какие знания нужно актуализировать для сознательного и прочного овладения способом дифференциального исчисления?
4) умения и Какие знания формируются при изучении способа?
Детальное обсуждение поставленных вопросов ведет к следующим выводам:
Сознательное усвоение способа дифференциального исчисления нереально без введения фундаментальных понятий, таких, как приращение функции и приращение аргумента, отношение этих приращении, производная, тангенс угла наклона касательной, совершённой к графику функции в указанной точке, предельный переход.
Способ дифференциального исчисления есть главным способом изучения разных процессов, решения разного класса задач, исходя из этого обучающимся нужно знание всех названных понятии. Ответ задач разрешает сделать интуитивно ясными такие понятия, как непрерывность функции, производная, геометрический и применение и механический смысл производной ее к приближенным вычислениям; сформулировать критерии убывания и возрастания функции, показатели максимума и минимума. Очень ответственным есть ответ учебно-практических задач средствами матанализа, поскольку на этом материале обучающихся знакомят с построениями математических моделей и их ответами.
Для успешного и сознательного овладения способом нужно актуализировать умения и знания обучающихся.
Знания:
— функции числового довода;
— функции и приращения аргумента;
— скорости неравномерного перемещения, средней скорости, мгновенной скорости;
— таблицы производных элементарных функций.
Умения:
— обнаружить значение функции в точке;
— обнаружить приращение функции по заданному приращению довода;
— обнаружить отношение приращения функции к приращению довода при заданных условиях;
— обнаружить среднюю скорость неравномерного перемещения.
В следствии изучения способа обучающиеся должны приобрести знания:
— определений понятия производной, точки максимума, точки минимума;
— метода нахождения производной, составления уравнения касательной к кривой в указанной точке;
— построения исследования графика и плана функций;
— главных формул дифференцирования, включая сложную функцию;
— интеграла и геометрического смысла производной;
— физического смысла производной;
— достаточного условия возрастания (убывания) функции.
Считается, что обучающиеся овладели способом, в случае, если в следствии изучения материала у них удалось организовать умения:
— обнаружить производную функцию в точке и на отрезке;
— применять понятие производной для изучения особенностей функции;
— устанавливать темперамент трансформации функции по символу производной;
— выявлять точки, странные на экстремум;
— вычислять громаднейшее (мельчайшее) значение функции на отрезке;
— использовать способ дифференциального исчисления для ответа сюжетных задач (математических и физических);
— использовать понятие производной для приближенных вычислений.
IV. Вышеуказанные цели и задачи позволяют выделить «ядерный» и сопутствующий материал, что разрешит обучающимся усвоить разглядываемый способ.
«Ядерным» материалом являются определения понятия производной и метод нахождения производной.
Сопутствующим материалом в первом случае — примеры вычисления производных элементарных функций, дифференцируемость функций.
Обучение способу дифференциального исчисления не должно сводиться к сообщению определения производной и на базе определений вычислениям производной. Дабы обучающиеся убедились, что дифференцирование вправду есть способом матанализа, нужно разглядеть разные по требованиям и фабуле задачи из различных областей знаний.
Приведем примеры таких задач:
Задача 1. Выяснить скорость тела, движущегося прямолинейно по закону (м), в момент времени t=5 с.
Задача 2. В узком неоднородном стержне длиной 35 см масса (в граммах) распределена по закону ,где l — протяженность части стержня, отсчитываемая от начала. Отыскать плотность в точке, отстоящей от начала на 3 см.
Задача 3. Закон свободного падения тела в пустоте определяется формулой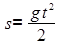 
, где g — постоянная величина. Отыскать скорость этого перемещения в некий фиксированный момент времени .
Анализ ответа приведенных задач разрешает понять, что при поиске ответов на поставленные требования любой раз выполнялась одинаковая последовательность операций. Возможно привести еще довольно много задач из техники, физики, для ответа которых нужно вычислять предел отношения приращения функции к приращению довода, в то время, когда последнее пытается к нулю. Выяснилось целесообразным выделить таковой предел, дать ему термин «производная» и изучить его фундаментальные особенности. По окончании введения термина формулируется определение производной, которое есть конструктивным, что разрешает «выстроить» метод вычисления производной в точке.
На базе определения производной формулируются теоремы о дифференцировании суммы, произведения, частного двух функций, рассмотрен частный случай дифференцирования сложной функции («внутренняя» функция — линейная) и постулируется, что это правильно и в общем случае.
3адание 2.
1) Установите, какие конкретно знания нужно актуализировать для понимания геометрического смысла производной.
2) Составьте серию задач, благодаря которой раскрывается геометрический суть производной.
3) Выясните, какие конкретно свойства функций изучаются посредством производной.
4) Составьте серию задач, благодаря которой вырабатывается аппарат данного способа.
5) Выясните, какие конкретно формы контроля действенно применять для определения сформированности способа.
Перечисленные задания для независимой работы предполагают групповую форму работы.
V. Потом рассматривается возможность применения способа дифференциального исчисления при изучении разных вопросов математики, раскрывается методика установления межпредметных связей.
Реализовать эти цели возможно при ответе следующих методических задач:
3адание 3.
1) Создайте серию тестовых задач на экстремум, которая разрешит узнать алгоритмическое предписание, благодаря которому в будущем будет осуществляться ответ таких задач.
2) Создайте методику формирования умения использовать изученный способ для составления уравнения касательной к графику функции в указанной точке, выясните шаги метода.
3) Установите, на каких задачах целесообразно продемонстрировать использование способа дифференциального исчисления для приближенных вычислений значений функции.
4) Приведите примеры физических, технических задач, на которых возможно продемонстрировать установление межпредметных связей.
В следствии анализа нескольких серий задач формулируется предписание ответа текстовых задач на нахождение громаднейшего (мельчайшего) значения. Предписание имеет следующие шаги:
— установить переменные и постоянные, применяемые в задаче, и установить, какая из переменных исследуется;
— составить математическую модель задачи (в этом случае функцию, громаднейшее либо мельчайшее значение которой требуется выяснить);
— отыскать производную функции;
— вычислить критические точки функции;
— выбрать критические точки, каковые принадлежат промежутку;
— вычислить значение функции в критических точках, лежащих в промежутка и на его финишах;
— установить вид экстремума в критических точках в промежутка посредством достаточного-условия экстремума;
— из всех взятых чисел выбрать мельчайшее (громаднейшее);
— записать ответ.
направляться обратить внимание на то, что полученное предписание не будет усвоено обучающимися формально, если оно есть следствием ответа серии математических задач.
Результатом ответа второй методической задачи есть предписание, складывающееся из шагов:
— отыскать производную функции;
— вычислить значение производной в указанной точке;
— сравнить значение производной с нулем;
а) в случае, если значение производной в разрешённой точке вычислить запрещено, то или касательную в данной точке совершить запрещено, или касательная перпендикулярна оси x, ее уравнение ;
б) в случае, если значение производной равняется нулю, то касательная в данной точке параллельна оси x,ее уравнение ;
в) в случае, если производная существует и ее значение превосходно от нуля, то в данной точке возможно совершить касательную к кривой, наклоненную к оси x;
— вычислить значение функции в указанной точке;
— составить выражения и ;
— из взятых выражений составить равенство.
Остановиться нужно на частичном ответе четвертой методической задачи, привести примеры лишь применения производной к ответу физических и технических задач.
3адание 4. Какими математическими задачами возможно продолжить предложенный перечень математических задач и какова должна быть методика их решения, дабы возможно было вычислять, что обучающиеся знают значение способа матанализа для других областей знаний?
Примеры задач:
1. Вычислить работу электрического тока, напряжение которого изменяется со временем.
2. Протяженность стержня равна 10 см, а его линейная плотность в точке, находящейся на расстоянии x см от левого финиша, равна (г/см). Выяснить массу стержня.
Итоговое задание. Создайте содержание учебного материала с при влечением данных из истории развития матанализа, на базе которого возможно продемонстрировать различие способов изучения особенностей функций элементарными средствами (посредством неравенств и уравнений) и посредством способов матанализа.
Литература: [5], [9], [10], [50], [96], [115], [37], [70].
Глава III