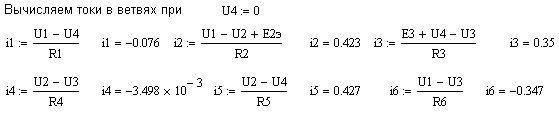Фундаментальными законами теории цепей наровне с законом Ома являются законы баланс токов в разветвлениях (первый закон Кирхгофа) и баланса напряжений на замкнутых участках цепи (второй закон Кирхгофа).
Режим электрической цепи произвольной конфигурации абсолютно определяется первым и вторым законами Кирхгофа. Законы Кирхгофа пригодны для ответа любых электротехнических задач (для постоянного и переменного токов, нелинейных цепей, переходных процессов).
Распределение токов и напряжений в электрических цепях подчиняется этим законам, каковые должны быть основательно усвоены для отчетливого понимания всего курса теории цепей.
Для каждой электрической цепи возможно выбрать совокупность свободных контуров. Контуры выбираются последовательно так, дабы в каждом была хотя бы одна ветвь, не входящая в уже рассмотренные контуры.
При выборе свободных контуров заданную схему цепи комфортно изображать в виде графа. Одним из способов определения числа контуров есть построение дерева схемы, а после этого поочередно добавляются главные ветви (это ветви графа, не входящие в состав дерева). Любой контур, образуемый добавлением новой ветви, есть свободным, поскольку он отличается от прошлых контуров новой ветвью. Вторым методом определения числа свободных контуров, достаточных для расчета схемы, есть построение поочерёдное размыкание и графа основных ветвей, пока не окажется дерево схемы.
Первый закон Кирхгофа: алгебраическая сумма токов любого узла электрической цепи равна нулю
,
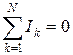где ? ток k-ой ветви, подключенной к узлу, N – число ветвей, входящих в узел.
В случае, если электрическая цепь имеет N ветвей и n узлов, то, в соответствии с первым законом Кирхгофа, для нее возможно взять (n – 1) линейно —
свободных уравнения.
Первый закон Кирхгофа высказывает тот факт, что в узле заряд не накапливается и не расходуется. Сумма зарядов, приходящих к узлу, равна сумме зарядов, уходящих от узла за одинаковый временной отрезок.
Первый закон Кирхгофа применим не только к узлу, но и к любому контуру либо замкнутой поверхности, охватывающей часть электрической цепи, поскольку ни в каком элементе цепи, ни в каком режиме электричество одного символа не имеет возможности накапливаться.
Второй закон Кирхгофа: алгебраическая сумма ЭДС любого замкнутого контура равна алгебраической сумме напряжений на остальных элементах этого контура
,
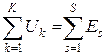где ? напряжение на k-ом элементе контура, ? ЭДС напряжения этого контура, K – число элементов контура (не учитывая S ? числа ЭДС, включенных в контур).
В соответствии со вторым законом Кирхгофа, для электрической цепи возможно взять N – (n ? 1) линейно-свободных уравнений.
Для определения числа свободных независимых контуров и узлов электрической цепи и, следовательно, числа свободных уравнений, составляемых на основании законов Кирхгофа, пользуются тем событием, что для линейной независимости совокупности уравнений достаточно, дабы каждое из входящих в совокупность уравнений отличалось от остальных хотя бы одной переменной. Этому условию удовлетворяет совокупность основных сечений графа, поскольку каждое из основных сечений m, соответствующих выбранному дереву, отличается; от вторых основных сечений, по крайней мере, одной ветвью, то есть ветвью дерева, входящей в данное основное сечение.
Для линейной независимости уравнений, составляемых на основании второго закона Кирхгофа, достаточно, дабы каждое из этих уравнений отличалось от остальных хотя бы одним напряжением. Следовательно, чтобы выделенная совокупность контуров была свободной, достаточно, дабы любой контур отличался от остальных хотя бы одной ветвью. Этому требованию удовлетворяет совокупность основных контуров, соответствующих какому-либо дереву графа, поскольку любой из основных контуров отличается от других, по крайней мере, соответствующей ему основной ветвью. Так как число основных контуров, соответствующих любому-дереву графа, p=N – n +1, то в каждой цепи возможно выделить n свободных контуров и составить для них p линейно свободных уравнений баланса напряжений.
Так, неспециализированное число линейно свободных уравнений, каковые возможно составить для произвольной цепи на основании законов Кирхгофа, выясняется равным числу ветвей разглядываемой цепи:
m+p = (n – 1)+(N – n +1) =N.
В связи с тем, что использованное достаточное условие линейной независимости совокупностей уравнений не есть нужным, для каждой электрической цепи возможно отыскать и другие системы свободных сечений и контуров, не совпадающие ни с одной из главных главных сечений и систем контуров графа разглядываемой цепи.
Второй закон Кирхгофа есть следствием закона сохранения энергии и отражает тот факт, что энергия, затраченная сторонними силами на перенос произвольного заряда в источников, входящих в контур, равна энергии, затрачиваемой источниками на перенос этого заряда через пассивные элементы контура.
направляться выделить, что закон сохранения энергии выполняется при переносе заряда по любому замкнутому пути (не обязательно абсолютно проходящему через ветви цепи). Исходя из этого уравнения по второму закону Кирхгофа возможно составить для любой совокупности элементов, образующих путь для электрического тока от произвольно выбранного узла (а) электрической цепи к узлу (б) с учетом напряжения между конечными точками этого пути иаб.
Так как число и вид уравнений, составленных на основании законов Кирхгофа, не зависят от того, какие конкретно элементы входят в состав цепи, а определяются лишь ее топологическими изюминками, то уравнения баланса токов и напряжений возможно использовать для математического описания процессов в моделирующих цепях, составленных из двухполюсных элементов любого типа (как линейных, так и нелинейных) при любой форме токов и напряжений свободных источников.
На основании законов Кирхгофа для каждой цепи возможно составить пара разных совокупностей линейно свободных топологических уравнений. Совокупностью свободных узлов либо совокупностью свободных контуров именуют каждые контуров цепи и совокупности узлов, для которых возможно составить совокупности линейно свободных уравнений по законам Кирхгофа. Определение числа свободных контуров и узлов, и выделение совокупностей соответствующих контуров и узлов являются главными задачами топологии цепей.
В случае, если известны все ее конфигурация и элементы цепи, а требуется выяснить токи, то при составлении уравнений по законам Кирхгофа рекомендуется придерживаться таковой последовательности:
- нумеруются узлы цепи; выбирается узел, потенциал, которого принимается известным (балансный либо нулевой узел), в большинстве случаев, равным нулю;
- для каждой ветви выбирается условно-хорошее направление тока и согласованное с ним направление напряжения;
- выбираются положительные направления и независимые контуры их обхода;
- для каждого узла, за исключением узла с заданным потенциалом, записываются уравнения по первому закону Кирхгофа. В этих уравнениях однообразные символы должны быть забраны для токов, имеющих однообразные хорошие направления довольно узловой точки. В большинстве случаев, токи, направленные к узлу, учитывают со знаком минус, а от узла – со знаком плюс;
- записываются уравнения по второму закону Кирхгофа. Хорошие символы принимаются для токов и ЭДС, хорошие направления которых совпадают с произвольно выбранным направлением обхода контура [2 ? 4].
Пример расчета электрической схемы на базе законов Кирхгофа
Разглядим пример расчета схемы со значениями элементов, представленной на рис. 3.1. Электрическая схема содержит источник тока Ik2, нагруженный на сопротивление R2. По второму закону Кирхгофа при составлении уравнений источник тока не имеет возможности входить в контур. Исходя из этого преобразуем его в эквивалентный источник ЭДС, применяя закон Ома (рис. 3.2)
. (3.1)
На рис. 3.3 приведена полученная схема с указанными хорошими направлениями контурных токов I11, I22 и I33, и токов в ветвях: i1, i2, i3, i4, i5 и i6.
Параметры схемы:
R1 = 6 Ом, R2 = 17,5 Ом,
R3 = 11 Ом, R4 = 3 Ом,
R5 = 5 Ом, R6 = 7,5 Ом,
| E3 |
Е2 = 6,5 В, Е3 = 6 В,
Ik2 = 0,2 А.
Рис. 3.1. Схема для значения и расчёта параметров элементов
Рис. 3.2. Преобразование источника тока в эквивалентный источник ЭДС
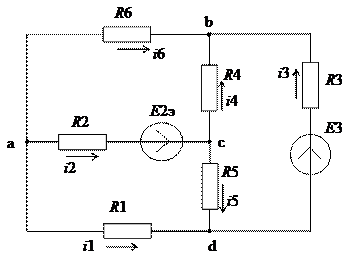
Рис. 3.3. Преобразованная схема с заданными направлениями токов в ветвях
В схеме на рис. 3.3 четыре узла a, b, c, d. Узел d принимаем за узел
с нулевым потенциалом. По первому закону Кирхгофа для каждого узла, не считая нулевого, составляем n – 1 = 3 уравнения, где n – количество узлов
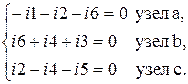(3.2)
Определяем свободные контуры и выбираем направление их обхода. Количество уравнений по второму закону Кирхгофа равняется количеству свободных контуров в схеме либо выражается формулой N – (n ? 1), где N ? число ветвей. Применяя второй закон Кирхгофа, составляем для каждого контура уравнение
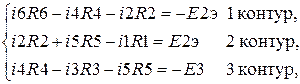(3.3)
где R1…R6 – сопротивления ветвей схемы, E2э и E3 – напряжения источников ЭДС схемы во втором и в третьем контуре, соответственно.
Общее рещение совокупностей уравнений (3.2) и (3.3) позволит найти численные значения искомых токов в ветвях.
Выразим из (3.2) токи i4, i5 и i6 через i1, i2 и i3, возьмём
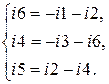(3.4)
Подставим во второе уравнение совокупности (3.4) выражения для тока i6, возьмём
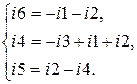(3.5)
В третье уравнение совокупности (3.5) подставим выражение для тока i4. Совсем возьмём
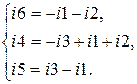(3.6)
Подставим значения токов i4, i5, i6, определяемых совокупностью (3.6) в (3.3). По окончании проведения элементарных арифметических преобразований приобретаем совокупность уравнений
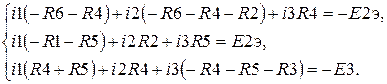(3.7)
Совокупность уравнений (3.7) складывается из трех уравнений и содержит три малоизвестных тока i1, i2 и i3, исходя из этого для ее решения возможно применять узнаваемые способы [6]: способ исключения Гаусса, способ Крамера, либо способ обратной матрицы.
Ответ совокупности уравнений (3.7) позволит найти токи i1, i2 и i3, а токи i4, i5 и i6 рассчитываются из совокупности (3.6).
Проводить расчеты линейных электрических цепей аналогичных схеме, приведенной на рис. 3.1. комфортно с применением средств MathCAD. Разглядим ответ совокупности уравнений (3.7) довольно токов i1, i2 и i3 и нахождение значений токов i4, i5 и i6 в MathCAD. Для решения совокупности уравнений (3.7) будем применять способ обратной матрицы, для этого представим совокупность (3.7) в матричном виде
, (3.8)
где I= (i1 i2 i3)Т – вектор токов, E = (–E2э E2э –E3)T – вектор ЭДС,
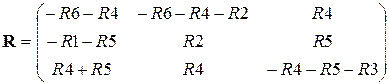— матрица сопротивлений,
Т – символ транспонирования.
Вектора токов I возможно выяснить из соотношения [6]
, (3.9)
где R-1 – обратная матрица R.
Примерный листинг программы в MathCAD имеет форму:
Способ контурных токов
Для расчета сложной электрической цепи возможно ограничиться совместным ответом только N – (n ? 1) свободных уравнений, составленных на базе второго закона Кирхгофа, воспользовавшись способом контурных токов.
Сущность способа содержится в том, что в нем реализуется принцип применения промежуточных переменных, число которых меньше, чем число искомых переменных. Наряду с этим осуществляется переход от настоящих токов рассчитываемой цепи (их число равняется N) к контурным токам (их число определяется числом свободных контуров и равняется N – (n ? 1)).
Контурный ток – это условный расчетный ток, имеющий однообразное значение на всех участках заданного контура. Для контура с источником тока уравнения не составляются, исходя из этого их, как и в прошлом способе, преобразовывают в источник ЭДС.
Для определения токов в ветвях способом контурных токов достаточно ввести в расчет контурные токи и составить уравнения лишь на основании второго закона Кирхгофа. При замене токов в ветвях контурными токами первый закон Кирхгофа выполняется, поскольку любой контурный ток в одной из ветвей контура направлен к узлу, а в второй ? от того же узла.
Сокращенная совокупность уравнений электрического равновесия цепи, составленная довольно малоизвестных контурных токов, именуется совокупностью контурных уравнений цепи.
При применении способа контурных токов сумму комплексных сопротивлений, входящих в контур, принято именовать собственным сопротивлением контура, а комплексное сопротивление, находящиеся в собствености в один момент двум контурам – неспециализированным сопротивлением этих контуров.
Неспециализированное сопротивление берется со знаком плюс, в случае, если контурные токи разглядываемых контуров протекают через неспециализированные для этих контуров ветви в однообразном направлении; в случае, если контурные токи в неспециализированных ветвях имеют противоположные направления, то неспециализированное сопротивление берут со знаком минус. В случае, если контуры не имеют неспециализированных ветвей, то их неспециализированное сопротивление равняется нулю.
Хорошие направления контурных токов задаются произвольно. Направление обхода каждого контура принимается в большинстве случаев совпадающим с выбранным хорошим направлением контурного тока. Исходя из этого при составлении уравнения по второму закону Кирхгофа падение напряжения от данного контурного тока в собственном сопротивлении контура берется со знаком плюс. Падение напряжения от тока смежного контура
в общем сопротивлении берется со знаком минус, в случае, если контурные токи
в этом сопротивлении направлены встречно.
При определении контурных токов составляют уравнения по второму закону Кирхгофа для каждого свободного контура и решают их довольно контурных токов.
В случае, если заданная электрическая схема содержит q свободных контуров, то на основании второго закона Кирхгофа получается совокупность из q уравнений
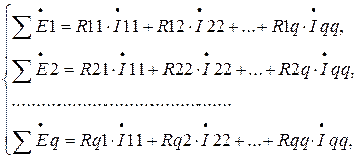(3.10)
где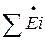 
? контурная ЭДС (в общем случае есть комплексной величиной) – алгебраическая сумма ЭДС, действующих в данном контуре; ЭДС, совпадающие по направлению с направлением обхода, берутся со знаком плюс, а направленные встречно – со знаком минус; Rii – собственное сопротивление контура i; Rik – неспециализированное (обоюдное) сопротивление контуров i и k.
Личные сопротивления Rii войдут со знаком плюс, потому, что обход контура принимается совпадающим с хорошим направлением контурного тока . Неспециализированные сопротивления Rik войдут со знаком минус, в то время, когда токи и направлены в них встречно.
Разбирая выражения (3.10), нетрудно установить, что все контурные уравнения имеют однообразную структуру: левая часть уравнении, составленного для i-го контура, является суммой участников, один из которых равен произведению контурного тока i-гo контура на его собственное сопротивление, а остальные – произведениям контурных токов вторых контуров на неспециализированные сопротивления i-гo этих контуров и контура; правая часть уравнения i-гo контура содержит лишь один член – контурную ЭДС этого контура.
Уравнения (3.10), высказывающие второй закон Кирхгофа, записав в предположении, что источниками электроэнергии помогают источники напряжения. При наличии в электрической схеме источников тока последние смогут быть заменены эквивалентными источниками напряжения. В случае, если проводимости источников тока равны нулю, то целесообразно в этом случае выбрать заданные токи в качестве контурных, тогда число малоизвестных контурных токов и соответственно число уравнение уменьшится на число заданных токов.
В случае, если в заданной электрической схеме имеются параллельные ветви, то замена их эквивалентным комплексным сопротивлением уменьшает число контуров (за счет тех, каковые образованы параллельными ветвями).
Электрические цепи смогут быть планарными либо непланарными.
Планарная, либо плоская, электрическая цепь возможно вычерчена на плоскости в виде схемы с неперекрещивающимися ветвями. В некоторых случаях пересечение в электрической схеме, являющееся результатом принятого метода начертания схемы, устраняется при втором методе изображения данной планарной электрической цепи. Непланарная электрическая цепь не может быть вычерчена на плоскости в виде схемы с неперекрещивающимися ветвями.
В случае, если направление контурных токов во всех контурах планарной электрической цепи одинаково, к примеру сходится с ходом часовой стрелки, то неспециализированные сопротивления смежных контуров входят в совокупность уравнений (3.10) со знаком минус, поскольку контурные токи смежных контуров направлены в неспециализированных ветвях встречно. Направление контурных токов по ходу часовой стрелки принимается во всех контурах, не считая внешнего контура, охватывающего всю схему. В последнем контурный ток направляется против часовой стрелки. Это правило, но, не есть необходимым.
Ответ уравнений (3.10) относительно искомых контурных токов возможно отыскано способом Крамера [6]
, 
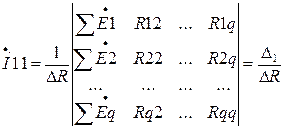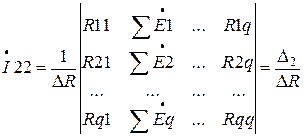и т.д., где определитель совокупности
.
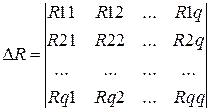На практике во многих случаях для ответа совокупности уравнений (3.10) возможно использован способ последовательных исключений малоизвестных либо способ Гаусса [6].
Для линейных цепей, состоящих лишь из сопротивлений, емкостей, независимых источников и индуктивностей напряжения, ма трица контурных сопротивлений квадратная, причем потому, что для таких цепей постоянно выполняется условие Rik= Rki, матрица Rik – симметрична довольно основной диагонали.
Так, зная структуру контурных уравнений и выделив главные контуры разглядываемой линейной цепи, нетрудно организовать совокупность контурных уравнений, не прибегая к составлению главной совокупности уравнений электрического равновесия цепи.
Пример расчета электрической схемы способом контурных токов
Разглядим пример расчета токов в ветвях электрической схемы, приведенной на рис. 3.1 способом контурных токов. Как и в прошлом способе, источники тока заменяем источниками напряжения и расчет проводим для схемы рис. 3.4, в которой в отличии от рис.3.3 введены контурные токи I11, I22 и I33. Потому, что рассчитываемая схема не содержит реактивных элементов, то символ комплексных размеров будем опускать
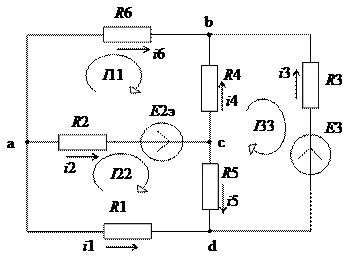
Рис. 3.4. Схема с заданными направлениями контурных токов и токов в ветвях
Расчеты будем проводить в следующей последовательности:
- выбираем свободные контуры, в нашем случае их три: abca, acda и bdcb (рис. 3.4), q = 3;
- за направления контурных токов принимаем хорошие направления токов (направления обхода контура по часовой стрелке);
- определяем личные и обоюдные сопротивления контуров:
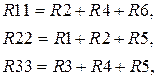
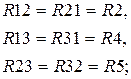
- вычисляем контурные ЭДС:
, , .
Решив совокупность (3.10) при q = 3 и определенных выше значениях сопротивлений и ЭДС, отыщем контурные токи
, 
, 
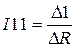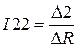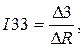
где ? определители совокупности (3.10), приобретаемые методом замены соответствующего столбца столбцом ЭДС и в разглядываемом случае имеющие вид
,
,
,
.
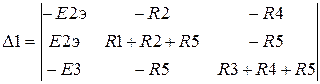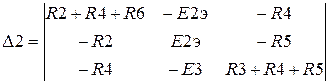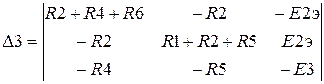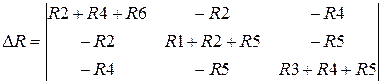Из отысканных значений контурных токов вычислим значения токов в ветвях (рис. 3.4) по соотношениям:
; ; ;
; ; . (3.11)
Листинг программы расчета для данных из прошлого примера имеет форму
Способ узловых потенциалов
В качестве свободных переменных, довольно которых формируют уравнения электрического равновесия цепи, возможно применять кроме этого так именуемые узловые напряжения, т.е. напряжения свободных узлов цепи довольно базового. Напряжения всех ветвей электрической цепи смогут быть выражены через ее узловые напряжения.
Способ формирования уравнений электрического равновесия цепи, в котором в качестве свободных переменных употребляются малоизвестные напряжения свободных узлов довольно базового, именуется способом узловых напряжений.
Способ узловых потенциалов рекомендуется использовать для расчета электрических цепей, у которых число узлов меньше числа свободных контуров. Данный способ основан на применении первого закона Кирхгофа
и обобщенного закона Ома. Расчетное число уравнений определяется числом узлов цепи и образовывает (n ? 1) уравнений.
Как и в способе контурных токов, тут кроме этого используются промежуточные переменные, в качестве которых употребляются узловые напряжения. Узловое напряжение – это напряжение между некоторым и любым
узлом схемы базовым узлом, потенциал которого принимают равным нулю. Хорошее направление узловых напряжений указывается стрелкой от разглядываемого узла к базовому. После этого записывают уравнения относительно напряжения узлов, число которых для любой схемы равняется (n ? 1), и решают их. Искомые токи ветвей определяются из отысканных напряжений узлов по обобщенному закону Ома.
Для любой электрической цепи, имеющей четыре узла, совокупность уравнений довольно узловых напряжений возможно записать в общем виде
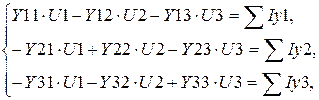(3.12)
где Ykk – личная проводимость k-го узла, Yik = Yki – обоюдная проводимость между i-м и k-м узлами, Uk – узловое напряжение k-го узла, ? узловой ток k-го узла (алгебраическая сумма токов, сходящихся в k-м узле).
Так, левая часть узлового уравнении, составленного для k -го свободного узла, имеется сумма участников, один из которых равен произведению узлового напряжения k -го узла на его собственную проводимость, а остальные – произведениям узловых напряжений вторых свободных узлов на обоюдные проводимости k -го этих узлов и узла. Правая часть каждого уравнения равна узловому току соответствующего узла.
Совокупность уравнений (3.12) возможно задать в матричном виде
, (3.13)
где матрица проводимостей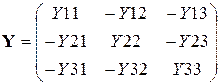 
, вектора узловых потенциалов U = (U1 U2 U3)T и токов .
Личная проводимость (Y11, Y22, Y33) определяется как комплексная проводимость всех ветвей, присоединенных к k-му узлу. Эти элементы находятся в основной диагонали матрицы проводимостей Y и принимают хорошие значения, в случае, если узловые напряжения направлены в базовый узел.
Обоюдная проводимость (Y12=Y21, Y23=Y32, Y13=Y31) определяется комплексной проводимостью между двумя узлами. В совокупности уравнений обоюдная проводимость постоянно записывается со знаком минус.
Узловой ток находят как алгебраическую сумму токов, создаваемых каждым источником ЭДС и источником тока, расположенными в ветвях, примыкающих к k-му узлу. Слагаемое в узловом токе имеет символ плюс, в случае, если соответствующий ему источник направлен к разглядываемому узлу и символ минус – в случае, если от него.
Уравнения (3.12)высказывающие первый закон Кирхгофа, записаны в предположении, что в качестве источников электроэнергии помогают источники тока. При наличии в электрической схеме источников напряжения последние должны быть заменены эквивалентными источниками тока.
В случае, если в схеме имеются ветви, которые содержат лишь ЭДС (проводимости таких ветвей вечно громадны), то эти ветви направляться разглядывать как источники малоизвестных токов, каковые после этого исключаются при сложении соответствующих уравнений. Дополнительными связями между малоизвестными узловыми напряжениями будут являться узнаваемые напряжения между узлами, равные заданным ЭДС.
При наличии лишь одной ветви с ЭДС и нескончаемой проводимостью целесообразно принять за базовый узел один из узлов, к каким примыкает эта ветвь; тогда напряжение другого узла делается известным и число малоизвестных уменьшается на одно.
Решив совокупность (3.12) либо матричное уравнение (3.13) способом Крамера довольно малоизвестных узловых напряжений, приобретаем выражения для напряжения k-го узла относительно базиса
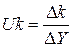, (3.14)
где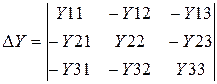 
? определитель матрицы проводимостей; Dk – определитель матрицы, приобретаемой из матрицы проводимостей Y методом замены k – го столбца матрицы Y на вектор узловых токов .
Уравнения совокупности (3.12) записаны в предположении, что источниками электроэнергии помогают источники тока. При наличии в электрической схеме источников напряжения последние должны быть заменены эквивалентными источниками тока.
Способ узловых потенциалов имеет преимущество перед способом контурных токов в том случае, в то время, когда число уравнений, записанных по первому закону Кирхгофа, меньше числа уравнений, записанных по второму закону Кирхгофа. В случае, если заданная электрическая схема имеет N ветвей и n узлов, то в соответствии с сказанным выше способ узловых напряжений воображает преимущество при (n – 1) (N – n + 1) либо, что то же самое, при 2(n ? 1) N.
Пример расчета электрической схемы способом узловых потенциалов
Разглядим на практике применение способа узловых потенциалов для расчета токов в ветвях электрической схемы на рис. 3.1.
Расчеты будем проводить в следующей последовательности:
- Заменим источники напряжения эквивалентными источниками тока, возьмём схему, приведенную на рис. 3.5.
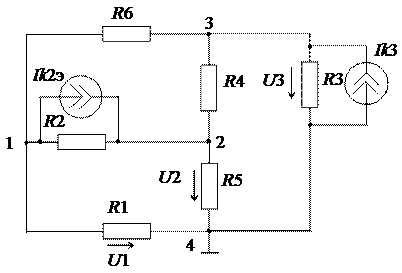Рис. 3.5. Схема с заданными узловыми потенциалами
При замене источников напряжения эквивалентными источниками тока, числовые размеры последних рассчитываем по соотношениям
, 
.
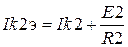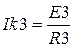- Принимаем за базовый ? узел d и вводим числовую нумерацию узлов, чтобы рассчитываемые параметры соответствовали совокупности уравнений (3.12). Так, базовым будет узел 4 (рис. 3.5).
- Отображаем на схеме стрелками направление узловых напряжений U1, U2, U3 – от каждого узла к базовому.
- Определяем величины собственных и обоюдных проводимостей узлов:
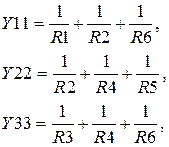
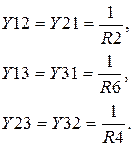
- Вычисляем узловые токи (алгебраическая сумма токов, создаваемых источниками тока, входящих либо исходящих из узла):
, , .
- Приобретаем совокупность уравнений (3.12) с учетов введенных выше параметров
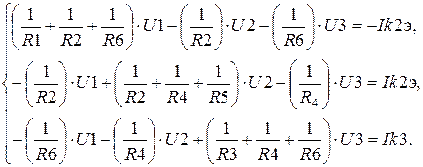(3.15)
- Решив совокупность уравнений (3.15) довольно малоизвестных значений узловых напряжений, вычислим токи в ветвях схемы по обобщенному закону Ома
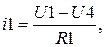
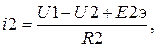
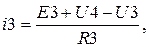
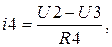
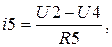
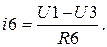
Листинг программы расчета в среде MathCAD значений токов в ветвях схемы способом узловых потенциалов имеет форму
