(25)
где
Sl— величина ближайшего к 50-процентной точке стимула, лежащего ниже ее; Sh— величина стимула, лежащего конкретно выше 50-процентной точки; Plи Ph— соответствующие вышеуказанным стимулам пропорции ответов.
Первый и третий квартили вычисляются по формулам:
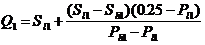 |
(26)
где Sl1— величина стимула, лежащего конкретно ниже 25-процентной точки; Sh1— величина стимула, лежащего конкретно выше 25-процентной точки; Pl1и Ph1 — соответствующие вышеуказанным стимулам пропорции ответов.
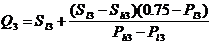 |
(27)
где S13 — величина стимула, лежащего конкретно ниже 25-процентной точки; Sh3 — величина стимула, лежащего конкретно выше 25-процентной точки; Pl3 и Ph3 — соответствующие вышеуказанным стимулам пропорции ответов.
В отечественном примере Md = 10,57 мм, Q1= 9,83 мм, Q3= = 11,33 мм.
Недочётами метода линейной интерполяции являются:
1) расточительность, поскольку из всех взятых в опыте данных употребляется лишь часть — к примеру, для определения Md достаточно иметь две точки;
2) отсутствие возможности взять правильную оценку показателей разброса – дисперсии либо межквартильного размаха – Q. В случае, если в опыте употребляется больше двух стимулов, возможно выяснить Q1и Q3, а вдруг допустить, что распределение частот ответов есть обычным, то возможно отыскать и величину стандартного отклонения через соотношение s = 1,483Q. Но при широком диапазоне применяемых стимулов и относительно малом их числе (около 5, как в отечественном примере) оценка Q будет не весьма правильной, следовательно, и значение s кроме этого.
Метод обычной интерполяции. В случае, если сделать более строгое допущение о форме психометрической функции, то есть, что она есть функцией обычного распределения, и в случае, если выразить масштаб оси ординат в единицах стандартного отклонения этого распределения, то психометрическая функция, имеющая S-образную форму в линейных координатах, преобразовывается в прямую линию. Затем появляется возможность отыскать все интересующие исследователя параметры прямой, подобно тому, как это делалось при линейной интерполяции. Но для этого необходимо в первую очередь преобразовать пропорции ответов P посредством таблиц обычного распределения в значения Z, воображающие собой нормированные по стандартному отклонению расстояния от стимульных точек до медианы. По окончании преобразования P в Z экспериментальные точки на графике, где по абсциссе отложен физический параметр стимула S, а по ординате — Z, смогут быть аппроксимированы прямой линией, которая проводится “на глазок” (данный метод не смотря на то, что и несложен, но значительно чаще дает только неотёсанное приближение), или рассчитывается посредством способа мельчайших квадратов. Данный способ дает возможность приобрести не только наилучшую аппроксимацию, но и статистически строго оценить степень “хорошести” подгонки взятой прямой к экспериментальным точкам.
Определение медианы, представленной в z-координатах психометрической функции, допустимо графическим и расчетным методом. За безотносительный порог (и PSE при измерении двухкатегориальным способом констант разностного порога) принимается величина стимула, которой соответствует Z = 0. Стандартное отклонение определяется как такая величина стимула, для которой Z = +1 либо Z = -1. Через стандартное отклонение возможно отыскать и величину полумежквартильного размаха — Q, т.к. их сообщение при обычного распределения описывается равенством
Q=0,674s (28)
Для иллюстрации этого метода обработки обратимся к нашему примеру (см. табл. 2). Графическое представление зависимости величины Z”два”от физического параметра стимула (т.е. психометрическая функция в обычных координатах) приведено на рис. 11.
Определение посредством графиков параметров психометрической функции методом обычной интерполяции не требует преобразования в z-координаты, в случае, если имеется в наличии вероятностная бумага. Метод изготовления таковой бумаги детально обрисован (Бардин, 1976).
Все нужные пороговые показатели смогут быть выяснены и аналитическим методом посредством соответствующих формул. Для этого возможно воспользоваться двумя способами.
Во-первых, возможно применить уже знакомый нам способ линейной интерполяции (сейчас в обычных координатах), что практически есть аналогом несложного графического ответа, в то время, когда мы не производим строгого построения аппроксимирующей прямой. Расчет параметров психометрической прямой производится по формулам (29), (30) и (31):
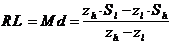 |
(29)
где
zlи zh— самые родные к нулю отрицательная и хорошая величины z, соответственно; Sl и Sh— стимулы, соответствующие zl и zh(т.е. величины ближайшего подпорогового и надпорогового стимулов).
Для оценки величины стандартного отклонения направляться забрать разность между точками на стимульной оси, соответствующими z=1 либо z=-1 и величиной порога — RL. Эти точки возможно вычислить так:
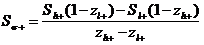 |
(30)
где zl+и zh+— ближайшие значения z, меньшие и громадные +1, соответственно;Sh+ и Sl+— стимулы, соответствующие zl+и zh+(т.е. ближайшие значения стимулов, ниже и выше Ss+).
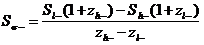 |
(31)
где zl- и zh- — ближайшие значения z, меньшие и громадные -1, соответственно; Sh- и Sl-— стимулы, соответствующие zl-и zh-(т.е. ближайшие значения стимулов, ниже и выше Ss-).
Оба значения Ss+и Ss-вычисляются в связи с тем, что полученная в опыте психометрическая кривая далеко не всегда является весьма хорошим приближением к кривой обычного распределения, и эти значения смогут расходиться. Исходя из этого в большинстве случаев для оценки разброса употребляется их среднее. В отечественном примере вычисления по приведенным формулам дали следующие размеры:
RL = 10.57 мм, Ss+и Ss-= 0.98 мм.
Во-вторых, воспользовавшись способом мельчайших квадратов, возможно выстроить наилучшую прямую, проходящую через экспериментальные точки. Эта задача решается легко в любом статистическом пакете методом исполнения процедуры построения несложной линейной регрессии. Вычислив так коэффициенты a и b линейной функции y=ax+b, мы легко отыщем малоизвестные “x” по известным “y” (z=0 , z=1 либо z=-1). Ясно, что потому, что точки Ss+и Ss- будут симметричны довольно RL, то достаточно вычислить только одну из них.
3. Варианты способа констант
Способ приращения. Изюминкой экспериментальной процедуры есть постоянное предъявление испытуемому стандартного стимула, к которому иногда добавляются приращения. Испытуемый отвечает, увидел ли он приращение, в терминах, к примеру, “Да”-”Нет”. Разностным порогом есть приращение стимула, заметное в 50% случаев. В способе приращений измеряется разностный порог реакции, воображающий собой половину промежутка неопределенности. Сомнения в отношении возможности применения промежутка неопределенности в качестве показателя различения уже высказывались выше.
В опытах, проводимых в поддержку нейроквантовой теории, практикуется вариант способа приращений, при котором в каждой экспериментальной серии употребляется только одна величина приращения. Наличие перерывов между экспериментальными сериями с различными размерами приращений есть недочётом этого способа, потому, что допускает направленное изменение черт испытуемого в отношении приращений различной величины.
Способ АБХ. В этом способе испытуемому предъявляются последовательно три стимула: первый обозначается А, второй — Б, третий — Х. Первые два стимула различаются величиной исследуемого параметра; в качестве третьего стимула (Х) употребляется или А, или Б. Испытуемый обязан ответить, какой из стимулов был Х. Способ АБХ при условии запрещения нейтральных ответов сводится к двухкатегориальному варианту способа констант. Данный способ активно используется в прикладных изучениях, где в большинстве случаев употребляются сложные стимулы, каковые нетренированный испытуемый затрудняется классифицировать в терминах “больше” — “меньше”, но отлично осознаёт и может выполнить задачу идентификации, в то время, когда от него не нужно вынесения суждения лишь по одному из в один момент изменяющихся сенсорных показателей при трансформации физических параметров стимула. В качестве оценки чувствительности в этом способе употребляется полумежквартильный размах — Q(2). Но эта оценка загрублена влиянием несенсорных факторов, приводящих к нестабильности критерия принятия испытуемым решения.
Для значительного уменьшения этого загрубления оценки Индлин (1979) предлагает ограничиваться в пределах одной постоянной части опыта применением одного сравниваемого стимула.
Методические советы по исполнению учебных заданий по теме
“Локализация точки на шкале”
Задание 1. Определение величины иллюзии Мюллера—Лайера способом минимальных трансформаций
Цель задания. Отработать способ минимальных трансформаций применительно к измерению разностного порога. Оценить величину иллюзии Мюллера—Лайера.
Методика
Аппаратура. Задание отрабатывается на IBM-совместимом персональном компьютере. Для предъявления сигнала “Внимание” употребляются головные телефоны, соединенные со звуковым синтезатором ПК. Для исполнения учебного задания употребляется компьютерная программа muler.exe.
Стимуляция. На экране дисплея предъявляются на одной горизонтальной линии две стрелы: обычный стимул (Sst) — стрела с наконечниками наружу, имеет длину 11 см и предъявляется в любой момент слева; и переменный стимул (Svar) — стрела с наконечниками вовнутрь и предъявляется в любой момент справа. Ее протяженность может изменяться в пределах от 17 до 10 см. Время экспозиции стрел — 1 с.
Процедура опыта. При отработке задания любой студент выступает сперва в роли испытуемого, а после этого обрабатывает личные экспериментальные эти. Испытуемый сидит на расстоянии 1 м до экрана дисплея. Любая проба начинается с появления звукового сигнала “Внимание”, после этого через 500 мс экспонируются обычный и переменный стимулы (1 с). Следующая проба начинается через 2 с, в течение которых испытуемый обязан дать собственный ответ, нажимая на одну из 3-х клавиш на клавиатуре компьютера. Задача испытуемого содержится в том, дабы сравнить переменный стимул со стандартным, применяя три категории ответов: “меньше”, “равняется” и “больше”. Для ответа смогут употребляться следующие клавиши: , , (на цифровой клавиатуре) либо клавиши управления перемещением курсора – , , .
Переменные стимулы предъявляются восходящими и нисходящими последовательностями, по 10 проб в каждом последовательности. Всего 20 восходящих и 20 нисходящих последовательностей.
Обработка данных. По окончании опыта студенту выдается компьютерная распечатка, в которой представлен полный протокол опыта, т.е. зафиксированы все ответы испытуемого на все стимулы (всего 400). Файл с взятыми разрешёнными легко найти: его имя соответствует фамилии испытуемого, написанной латинскими буквами, а расширение — mul, к примеру: ivanov.mul.
Согласно данным протокола любой студент обязан вычислить следующие показатели:
1) нижний (Llи Ll¯) и верхний (Lhи Lh¯) пороги в каждом последовательности стимулов;
2) нижний (Ll) и верхний (Lh) пороги по опыту в целом (см. формулы (5) и (6)); оценить разброс взятых пороговых значений, вычислив соответствующие значения стандартного отклонения — sl и sh;
3) IU и DL (формулы (7) и (8));
4) PSE (формула (9));
5) количественно оценить согласно данным опыта выраженность иллюзии, вычислив CE (формула (10)).
Для исполнения нужных статистических расчетов (среднее арифметическое и стандартное отклонение) направляться воспользоваться статистическим пакетом “Stadia” (директория “Stadia”, командный файл — stadia.exe). По окончании ввода взятых данных в электронную таблицу ( 40 значений Ll — в первую переменную и 40 значений Lh— во вторую) в меню статистических способов (F9) необходимо выбрать самый первый пункт — “Описательная статистика” и указать номера разбираемых переменных: в нашем случае их две — 1, 2. По окончании нажатия на клавишу на экране распечатывается множество статистических показателей, а также — среднее арифметическое и стандартное отклонение для каждой переменной.
В качестве дополнительного задания по работе с разрешёнными можно рекомендовать построение графиков трансформации пороговых значений в течение опыта, на которых в наглядной форме легко проанализировать вероятные тенденции трансформации верхнего и нижнего порогов, к примеру: этап врабатывания, другие стабилизации феномены и период ответов динамики исполнения данной сенсорной задачи. Для этого, возвратившись в электронную таблицу (блок редактора данных), необходимо надавить на клавишу F6 и перейти к построению нужного графика. В качестве типа графика выберите функциональный, потом укажите число графиков — 2 (один для Ll, второй для — Lh) и номера соответствующих им переменных (1 для первого графика и 2 — для второго); графики лучше нарисовать линиями, а разметку осей координат возможно не делать.
Задание 2. Измерение порога частоты слияния мельканий способом установки
Цель задания. Отработать способ установки применительно к измерению полного порога. Оценить величину критической частоты слияния мельканий.
Методика
Аппаратура. Задание выполняется на IBM-совместимом персональном компьютере, с параллельным портом которого соединен красный светодиод. Для исполнения учебного задания употребляется компьютерная программа kcm.exe.
Стимуляция. Светодиод расположен на расстоянии 1м от испытуемого. Мелькающий свет задается посредством подачи на него маленьких электрических импульсов длительностью 2 мс. Частота управляющих импульсов может изменяться испытуемым в диапазоне от 1 до 100 Гц с дискретностью 0.1 Гц.
Процедура опыта. При отработке задания любой студент выступает сперва в роли испытуемого, а после этого обрабатывает личные экспериментальные эти. Испытуемый сидит на расстоянии 1 м до экрана дисплея. Задача испытуемого содержится в том, дабы, регулируя частоту мелькания светодиода, установить пороговую (минимальную) величину частоты мелькания, при которой в первый раз появляется чувство постоянного свечения светодиода, т.е. отсутствие мельканий. Регулировка частоты мельканий осуществляется посредством клавиш управления курсором на клавиатуре ПК: клавиша помогает для уменьшения частоты, а клавиша — для ее повышения. В инструкции отмечают, что испытуемый может вольно регулировать частоту, переходя через пороговое значение и опять возвращаясь назад.
Опыт складывается из 2-х серий — тренировочной и главной. В тренировочной серии испытуемому даются две попытки для установки порогового значения: начать из очевидно надпорогового диапазона стимулов (5 Гц), а после этого — из очевидно подпорогового (60 Гц). При нахождении порога необходимо надавить на клавишу “пробел”. В главной серии испытуемый осуществляет 20 установок: по 10 из надпорогового и подпорогового диапазонов. В каждой следующей пробе частота начального стимула изменяется в случайном порядке.
Обработка данных. По окончании опыта студенту выдается компьютерная распечатка, в которой представлен протокол опыта, где зафиксированы результаты всех 20 установок. При жажде возможно отыскать и файл данных: его имя соответствует фамилии испытуемого, а расширение — kcm.
Согласно данным протокола любой студент обязан вычислить следующие показатели:
1) пороговую частоту слияния мельканий — RL, усреднив результаты всех 20 установок;
2) разброс пороговых значений, вычислив стандартное отклонение — ?;
3) статистическую неточность, допущенную при вычислении RL (формула (4)).
Нужные статистические вычисления производятся посредством статистической совокупности “Stadia” в меню “Описательная статистика” (см. задание 1.).
Задание 3. Измерение порога различения длительности тональных сигналов способом постоянных раздражителей. Изучение влияния несенсорных факторов на пороговые меры
Цель задания. 1. Практическая отработка способа на примере определения дифференциального порога при разных руководствах испытуемому. 2. Освоение процедуры вычислений разных пороговых мер, приобретаемых в этом способе (промежуток неопределенности, точка субъективного равенства, константная неточность). 3. Сравнение зависимости разных пороговых мер от несенсорных факторов.
Методика
Аппаратура. Задание отрабатывается на IBM-совместимом персональном компьютере. Для предъявления звуковых сигналов (тона частотой 1000 Гц) употребляются головные телефоны, соединенные со звуковым синтезатором ПК. Продолжительность стандартного стимула — 900 мс, продолжительность пяти переменных (сравниваемых) стимулов — 600, 750, 900, 1050 и 1200 мс.
Для исполнения учебного задания употребляется компьютерная программа mc.exe.
Процедура опыта. При отработке задания любой студент выступает сперва в роли испытуемого, а после этого обрабатывает личные экспериментальные эти. Опыт складывается из одной тренировочной и трех главных серий. Испытуемому последовательно предъявляются два звуковых стимула, его задача — сравнить их по длительности. Место стандартного и сравниваемого стимулов в паре изменяется в квази-случайном порядке. Продолжительность сравниваемого стимула кроме этого изменяется в квази-случайном порядке. Межстимульный промежуток — 500 мс. На протяжении звучания каждого из стимулов на экране монитора последовательно появляются номера стимулов в паре (1 — 2, 1 — 2 и т.д. ), что разрешает испытуемому выяснить, в какой момент времени необходимо давать ответ. В случае, если испытуемый не дал ответ в прошедшей пробе, то предъявление пары стимулов повторяется. Межпробный промежуток, за который испытуемому требуется дать ответ, применяя трехкатегориальную совокупность ответов (“первый больше”, “равны” и “первый меньше”), равен 2 с. Для ответа употребляются цифровые клавиши — , , .
Три главные серии отличаются друг от друга разными руководствами испытуемому, что ведет к трансформации его стратегии при выборе ответа. В значительной мере этот опыт повторяет известное изучение С. Фернбергера (цит. по: Бардин, 1976), в котором было четко продемонстрировано, что при применении в способе констант трехкатегорийной совокупности ответов значение дифференциального порога значительно зависит от сугубо несенсорных факторов.
Инструкция к первой серии — нейтральная: испытуемый обязан давать ответы в соответствии с своим впечатлениям. Инструкция ко второй серии запланирована на минимизацию ответов в промежуточной категории (“равняется”): испытуемый обязан пользоваться данной категорией в тех редких случаях, в то время, когда, не обращая внимания на все усилия, он не может различить сигналы по длительности. Инструкция к третьей серии запланирована на максимизацию ответов “равняется”: к данной категории нужно относить все ощущения равенства либо сомнения в сравнении переменного стимулов и стандарта; причем ответы “больше” и “меньше” необходимо давать только при громадной уверенности в отличии стимулов.
В каждой из этих серий испытуемым предъявляется 150 проб (по 30 предъявлений каждого переменного стимула). По окончании каждой серии делается 2—3-минутный паузу.
Обработка результатов. По окончании окончания опыта испытуемый приобретает компьютерную распечатку, где для каждой серии приводятся частоты ответов “больше ”, “равняется” и “меньше” для каждого из пяти переменных стимулов.
По каждой серии обработка результатов осуществляется следующим образом:
1. Строятся два графика с психометрическими кривыми в линейных координатах. На первом графике строятся психометрические кривые для 3-х категорий ответов (см. рис. 7—9). На втором — для 2-категориального варианта, наряду с этим нейтральные ответы делятся поровну между пропорцией ответов “больше” и “меньше” (достаточно выстроить лишь одну кривую — для ответов “больше”).
2. Для расчета всех пороговых показателей (IU, DL, PSE, CE) употребляется графический способ, основанный на методе линейной интерполяции.
3. После этого, применяя 2-категориальный вариант расчетов, строятся психометрические функции в обычных координатах для ответов “больше”.
Посредством способа мельчайших квадратов по пяти экспериментальным точкам проводится наилучшая прямая, проходящая через эти точки. Для этого целесообразно воспользоваться статистическим пакетом “Stadia”. В редакторе данных длительности переменного стимула заносятся в первую переменную (это будут значения X ), а z-оценки — во вторую (это будут значения Y). После этого переходят в меню статистических процедур (F9) и выбирают опцию “Несложная регрессия (тренд)”. Войдя в нее, необходимо указать номера переменных (1,2), а после этого указать тип функции для построения регрессии — линейная. Затем программа выстроит для вас математическую модель ваших данных, воображая их в виде уравнения прямой: Y = a0 + a1X. Взяв коэффициенты a0 и a1, возможно легко выстроить на графике аппроксимирующую прямую. Статистическая оценка адекватности сделанной линейной аппроксимации приводится внизу экрана результатов анализа. Не выходя из программы, возможно легко вычислить и все нужные показатели: PSE, Ss+и Ss- . Это указывает, что по уравнению регрессионной прямой необходимо отыскать 3 малоизвестных X по трем известным Y: z=0, z=+1 и z=-1. С целью проведения расчетов необходимо опять возвратиться в меню статистических способов и, выбрав ту же опцию (“Линейная регрессия”), указать второй порядок переменных — 2,1. Это будет означать , что в качестве X мы выбираем z-оценки, а в качестве Y — продолжительность стимула. По окончании расчета нового регрессионного уравнения необходимо последовательно ввести три вышеуказанные величины z, и вычислять итог вычисления PSE, Ss+и Ss-.
Потом вычисляются все нужные пороговые показатели: IU, DL и CE.
4. Результаты обработки по каждой серии сводятся в итоговую таблицу.
Так в данной таблице в компактном виде должны быть представлены все полученные пороговые показатели в зависимости от инструкции (“твёрдая”, “нейтральная” и “либеральная”) и способа обработки (3-х категориальный, 2-х категориальный и интерполяция в обычных координатах).
В случае, если проводится обработка групповых результатов (см. выше), то эти, полученные по трем группам испытуемых, усредняются и кроме этого сводятся в одну неспециализированную таблицу.
Обсуждение результатов. На протяжении анализа взятых результатов направляться оценить действие для того чтобы замечательного несенсорного фактора как инструкция на разные пороговые показатели, и взглянуть, зависят ли вычисленные показатели от способа обработки результатов.
В выводах необходимо оценить ограничения и возможности способа констант применительно к задаче оценки сенсорной чувствительности.
Литература
Главная
1. Бардин К.В. Неприятность порогов чувствительности и психофизические способы. М.: Наука, 1976. С. 69—278.
2. Энген Т. Психофизика 1. Различение и методы // психофизики и обнаружение Проблемы. / Под ред. А.Г.Асмолова, М.Б.Михалевской. М.: Изд-во Моск. ун-та, 1974.
Дополнительная
1. Бардин К.В., Индлин Ю.А. Начала субъективной психофизики: В 2 ч. М.: Изд. ИП РАН, 1993.
2. Индин Ю.А. Современные способы субъективной оценки различий в звучаниях // Обзорная информация НИКФИ. Вып.1(34). М., 1979. С.4—24.
3. Михалевская М.Б., Скотникова И.Г. Способ подравнивания: зависимость мер чувствительности от сенсорной задачи. Вестн. Моск. ун-та. Сер. “Психология”. 1978. № 1. С.46-56.
4. Guilford J.P. Psychometric Methods. N.-Y.; Toronto; London: Mc-Grow-Hill, 1954. Р. 86—153.
Приложение 1
Требования к оформлению отчета по учебному заданию
1. Отчет пишется на стандартных страницах писчей бумаги. Все страницы заполняются лишь с одной стороны. Номера страниц проставляются в верхнем правом углу. Текст на странице ограничивается рамкой: сверху и снизу — 2—2.5 см, слева и справа — 2—2.5 см.
Любой отчет начинается с титульного страницы, что является обложкой работы. Сверху на нем указывается принадлежность студента к учебному заведению, факультету, специализации либо кафедре. В середине страницы указывается наименование изучаемой темы либо раздела и наименование учебного задания (к примеру: “Неспециализированный психотерапевтический практикум: психотерапевтические измерения. Способ минимальных трансформаций”). Ниже и справа указывается инициалы и фамилия студента, номер отвлечённой группы, инициалы и фамилия учителя. Внизу титульного страницы отмечают год исполнения работы.
Эта страница помогает кроме этого для отметок учителя о исполнении замечаний и учебного задания по поводу подготовленного студентом отчета.
2. Структура отчета о исполнении учебного задания в практикуме:
постановка проблемы и Теоретическое введение (не более 3-х страниц). В данном разделе отчета дается неспециализированная черта изучаемого способа, его характерных изюминок, даются определения нужных терминов.
Формулировка конкретных задач и цели работы в соответствии с неспециализированной проблемой, рассмотренной в теоретическом введении (не более 0.5 страницы).
Описание методики. В данный раздел входят следующие пункты: 1) сведения об испытуемом, время и дата проведения опыта; 2) описание использованной программного обеспечения и аппаратуры; 3) описание параметров стимуляции; 4) подробное описание процедуры опыта: какие конкретно стимулы предъявлялись, в каком порядке, какие конкретно ответы и в какой форме давал испытуемый; приводится инструкция испытуемому; в случае, если опыт складывался из нескольких серий, указывается их порядок. В том случае, если процедура опыта была нарушена, указывается обстоятельство.
В случае, если опыт проводился на компьютере, направляться указать имя файла результатов.
Результаты. В данной части нужно обрисовать полученные эти, способы их обработкии привести главные результаты. В случае, если употреблялись нестандартные методы обработки результатов, то их описанию стоит выделить особенное внимание. В случае, если употреблялись способы статистического анализа, то нужно привести соответствующие формулы либо сослаться на использованный статистический пакет при работе на компьютере. В последнем случае, в большинстве случаев, направляться привести стандартную распечатку взятых результатов обработки.
Итоговые результаты совершённых измерений сводятся в одну таблицу. Любая таблица должна быть пронумерована и иметь соответствующее наименование, где необходимо четко выразить главное содержание данной таблицы.
Картинки, иллюстрирующие главное содержание работы, должны быть кроме этого пронумерованы и начерчены на координатной бумаге. В том случае, если по рисунку производится вычисление каких-либо результатов (как, к примеру, при с психометрической функцией), то направляться обратить внимание на выбор подходящего масштаба. В случае, если рисунок делается посредством компьютерной программы, то стоит позаботиться о введении координатной сетки. На графиках должны быть указаны все параметры, нужные для однозначного понимания графика. Подрисуночные обозначения и подписи на графиках должны давать все данные, дабы не появлялась необходимость для понимания графика обращаться к тексту отчета.
таблицы и Рисунки рекомендуется делать на отдельных страницах.
выводы и Обсуждение результатов должны соответствовать задачам и целям работы. В том случае, если взят нестандартный и неожидаемый итог, то непременно направляться выделить особенное внимание его интерпретации и постараться растолковать обстоятельства его появления. В случае, если работа выполнялась в рамках какой-либо модели, то необходимо осуществить четкое заключение о соответствии взятых результатов ее версиям.
Выводы должны быть маленькими и конкретными.
Литературные ссылки оформляются в соответствии с требованиями, предъявляемыми ГОСТом к научным статьям.
Приложение 2
Таблица для перевода значений p в значения z
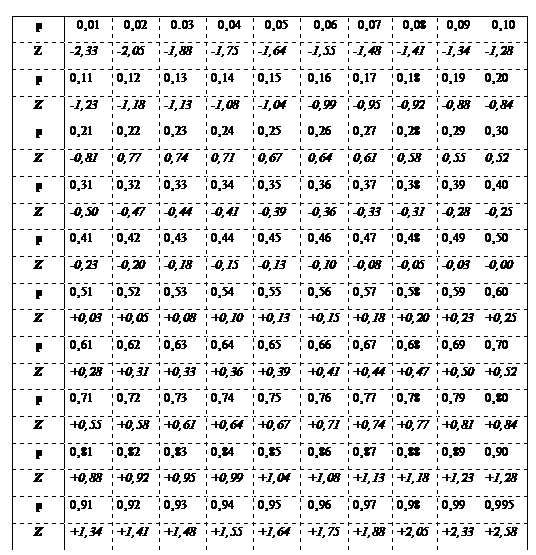 |
Глава 2. СПОСОБЫ ОБНАРУЖЕНИЯ СИГНАЛА
§ 1. Неспециализированные понятия
В данной главе рассматриваются способы, отличающиеся от прошлой группы способов новым подходом к локализации точки на психотерапевтической шкале, в противном случае говоря, вторым подходом к измерению граничного шкального значения, разделяющего имеющееся множество стимулов на два класса: обнаруживаемые и необнаруживаемые, различаемые и неразличаемые и т.п.