Для характеристики вращательного перемещения жёсткого тела около неподвижной оси введем понятие угловой скорости и углового ускорения. Алгебраической угловой скоростью тела в какой-либо момент времени именуют первую производную по времени от угла поворота сейчас, т.е. . Она есть величиной хорошей при вращении тела против часовой стрелки, поскольку угол поворота возрастает с течением времени, и отрицательной – при вращении тела по часовой стрелке, в силу того, что угол поворота наряду с этим убывает.
Модуль угловой скорости обозначают , тогда
Размерность угловой скорости устанавливаем в соответствии с уравнением (2.40):
В технике угловая скорость – это частота вращения, выраженная в оборотах в 60 секунд. За 1 60 секунд тело повернется на угол , в случае, если n – число оборота в 60 секунд. Поделив данный угол на число в минуте, возьмём
Алгебраическим угловым ускорением тела именуют первую производную по времени от угловой скорости либо . Модуль углового ускорения обозначим , тогда
Размерность углового ускорения приобретаем из уравнения (2.42):
Алгебраическую угловое ускорение и угловую скорость на картинках изображают дуговыми стрелками около оси вращения. Дуговая стрелка для угловой скорости показывает направление вращения тела, а дуговая стрелка для углового ускорения – направление, в котором возрастает алгебраическая угловая скорость.
- ускорения и Скорости точек тела
Известно уравнение вращения жёсткого тела около неподвижной оси (рис. 2.15). Расстояние s точки М в подвижной плоскости П по дуге окружности (траектории точки), отсчитываемое от точки , расположенной в неподвижной плоскости, выражается через угол зависимостью , где – радиус окружности, по которой перемещается точка. Он есть малейшим расстоянием от точки М до оси вращения. Его время от времени именуют радиусом вращения точки. У каждой точки тела радиус вращения остается неизменным при вращении тела около неподвижной оси. Алгебраическую скорость точки М определяется по формуле
а модуль скорости – по формуле
(2.43)
Скорости точек направлены по касательным к траектории и, следовательно, перпендикулярны радиусам вращения.
Скорости точек тела, расположенных на отрезке прямой ОМ, в соответствии с уравнением (2.15) распределяются по линейному закону. Они взаимно параллельны, и их финиши находятся на одной прямой, проходящей через ось вращения.
Ускорение точки разлагаем на касательную и обычную составляющие, т.е.
Касательное и обычное ускорения вычисляются по формулам
(2.44)
Обычное ускорение направлено по радиусу окружности к оси вращения. Направление касательного ускорения зависит от символа алгебраического углового ускорения.
Обозначив угол между полным ее радиусом и ускорением точки вращения, имеем
Угол для всех точек тела одинаковый. Откладывать его направляться от ускорения к радиусу вращения в направлении дуговой стрелки углового ускорения независимо от направления вращения жёсткого тела.
- Векторы угловой скорости и углового ускорения
Введем понятия векторов угловой скорости и углового ускорения тела. В случае, если — единичный вектор оси вращения, направленный в ее хорошую сторону, то векторы угловой скорости и углового ускорения определяют выражениями
Так как – постоянный по направлению и модулю вектор, то из уравнения (2.46) направляться, что
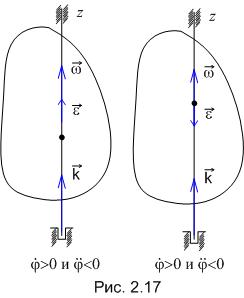
При и направления векторов и совпадают. Они оба направлены в хорошую сторону оси вращения Oz (рис. 2.17, а). В случае, если и , то они направлены в противоположные стороны (рис. 2.17, б). Вектор углового ускорения сходится по направлению с вектором угловой скорости при ускоренном вращении и противоположен ему – при замедленном. Векторы и возможно изображать в произвольных точках оси вращения. Они являются векторами скользящими.
- Векторные формулы для ускорения и скоростей точек тела
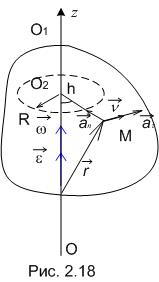
Выразим скорость, касательное, обычное и полное ускорения точки тела в векторной форме. Скорость точки по направлению и модулю возможно представить векторным произведением (рис. 2.18):
где – радиус-вектор точки М, совершённый из произвольной точки оси вращения Oz, к примеру точки О. Выражение (2.48) именуется векторной формулой Эйлера.
Из векторной формулы и определения ускорения Эйлера имеем
Учитывая, что
приобретаем
Первое слагаемое в уравнении (2.49) есть касательным ускорением, а второе – обычным, т.е.
Из определения скорости точки как мы знаем, что
где – радиус-вектор точки, приведенный из любой неподвижной точки, например, из любой точки на оси вращения тела, вращающегося около неподвижной оси. Но скорость точки при вращательном перемещении тела определяется по векторной формуле Эйлера:
Сопоставление двух формул для скорости точки дает формулу для вычисления производной по времени от вектора :
В данной формуле вектор имеет постоянный модуль, поскольку соединяет все время две точки жёсткого тела. Вектор , являясь угловой скоростью вращения жёсткого тела около неподвижной оси, делает кроме этого роль угловой скорости вращения вектора , жестоко скрепленного с телом.
Формула (2.51) остается честной кроме этого для вектора, начало которого находится в любой точке тела, а не только на оси вращения. По данной формуле вычисляется производная по времени от любого вектора, величина которого постоянна.
Тема 2.3. Плоское перемещение жёсткого тела
Плоским перемещением жёсткого тела именуют такое его перемещение, при котором любая его точка все время движется в одной и той же плоскости. Плоскости, в которых движутся отдельные точки, параллельны между собой и параллельны одной и той же неподвижной плоскости. Исходя из этого плоское перемещение жёсткого тела довольно часто именуют плоскопараллельным перемещением.
Пускай жёсткое тело совершает плоское перемещение, параллельное неподвижной плоскости (рис. 2.19). Тогда каждая прямая, перпендикулярная данной плоскости и жестоко скрепленная собственными точками с движущимся телом, будет двигаться поступательно, т.е. все точки данной прямой движутся одинаково.
Следовательно, для изучения перемещения точек, лежащих на разглядываемой прямой, достаточно изучить перемещение одной точки данной прямой, к примеру, точки М. Так, для изучения плоского перемещения жёсткого тела достаточно изучить перемещение фигуры в ее плоскости, параллельной неподвижной плоскости .
2.3.1. Уравнения плоского перемещения жёсткого тела
Отнесем перемещение фигуры S к неподвижной совокупности отсчета Oxy, находится в плоскости П. Положение фигуры в ее плоскости будет выяснено, в случае, если задать положения двух ее точек и либо положение отрезка, соединяющего эти точки (рис. 2.20).
Разумеется, что
Из равенства (2.52) направляться, что для определения положения отрезка достаточно знать каждые три координаты из четырех.
Положение фигуры в ее плоскости возможно выяснить в противном случае. Свяжем жестко с плоской фигурой совокупность координат . Положение данной совокупности будет выяснено, в случае, если известны положения начала и угол , образованный, к примеру, осью с неподвижной осью Ox (рис. 2.21).
При перемещении фигуры S в плоскости П координаты и угол являются функциями времени:
Равенства (2.53), определяющие положение фигуры, именуются уравнениями перемещения плоской фигуры либо уравнениями плоского перемещения жёсткого тела. Точка , выбранная для определения положения сечения S, именуется полюсом.
2.3.2. Разложение плоского перемещения жёсткого тела на поступательное и вращательное
Любое перемещение жёсткого тела, среди них и перемещение плоской ее плоскости и фигуры, бесчисленным множеством способов возможно разложить на два перемещения.
Настоящее плоское перемещение фигуры из положения I в положение II возможно любым, но его в любой момент возможно заменить двумя несложными плоскими перемещениями – поступательным и вращательным – так, дабы конечное положение плоской фигуры и в том и другом случае было одним и тем же. Поступательное перемещение
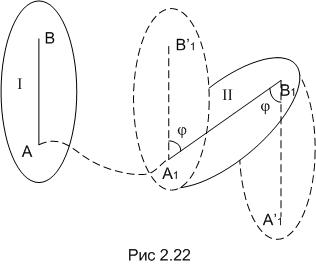зависит от выбора точки фигуры, вместе с которой совершается это поступательное перемещение, тогда как угол поворота около полюса не зависит от выбора полюса. На рис. 2.22 продемонстрированы случаи, в то время, когда за полюсы выбираются сперва точка А, а после этого точка В.
Рис.2.22
2.3.3. угловое ускорение и Угловая скорость тела
при плоском перемещении
Для характеристики вращательной части плоского перемещения жёсткого тела около подвижной оси, проходящей через выбранный полюс, подобно случаю вращения жёсткого тела около неподвижной оси, возможно ввести понятия угловой скорости и углового ускорения . В случае, если угол поворота около подвижной оси, проходящей через полюс, обозначить , то
Так как вращательная часть перемещения не зависит от выбора полюса, то и характеристики данной части перемещения – угловое ускорение и угловая скорость – кроме этого не зависят от выбора полюса.
Вектор угловой скорости при плоском перемещении фигуры направлен по подвижной оси так, дабы с конца его стрелки возможно было видеть вращение фигуры против часовой стрелки. Вектор углового ускорения при ускоренном вращении фигуры сходится с направлением вектора угловой скорости , а при замедленном вращении эти векторы имеют противоположные направления. Так как и не зависят от выбора полюса на плоской фигуре, то, следовательно, их возможно приложить в любой точке фигуры, не изменяя направлений и модулей этих векторов, т.е. и являются свободными векторами. Вектор углового ускорения есть первой производной по времени от вектора угловой скорости, т.е.
2.3.4. Скорости точек плоской фигуры
Зависимость между скоростями точек плоской фигуры устанавливается следующей теоремой:
Скорость любой точки плоской фигуры равна геометрической вращательной скорости скорости и сумме полюса данной точки около полюса.
б
Рис.2.23
Дабы выяснить скорость любой точки плоской фигуры, к примеру, точки В, точку А, скорость , принимаем за полюс (рис. 2.23, а).
Из неподвижной точки О совершим в точки А и В радиус векторы и . Во все время перемещения сохраняется зависимость
где – радиус-вектор точки В относительно полюса А. Вектор есть вектором постоянного модуля, поскольку расстояние между точками А и В жёсткого тела в ходе перемещения остается неизменным; данный вектор вращается вместе с телом с угловой скоростью .
Забрав производную по времени от равенства (2.56), возьмём
В этом выражении – скорость полюса А, а – вращательная скорость точки В около полюса А.
Вращательная скорость лежит в плоскости фигуры; она перпендикулярна отрезку АВ и направлена в сторону вращения плоской фигуры (рис. 2.23, б). Модуль вектора равен
Совсем имеем
2.3.5. Мгновенный центр скоростей
Точка плоской фигуры, скорость которой сейчас времени равна нулю, именуется мгновенным центром скоростей Р.
Приведем без доказательства теорему.
При плоском перемещении фигуры в ее плоскости в любой момент времени, в случае, если , существует мгновенный центр скоростей.
Такая точка P обязана пребывать на перпендикуляре AN, взятом при повороте вектора на угол 90 в направлении вращения фигуры (рис. 2.24), на расстоянии
В случае, если положение мгновенного центра скоростей Р сейчас времени известно, то приняв его за полюс и учитывая, что скорость его в этом случае равна нулю, возьмём следующие выражения для определения скоростей точек плоской фигуры (рис. 2.25):
По направлению скорость перпендикулярна отрезку , а скорость – отрезку .
Из уравнений (2.58) направляться, что
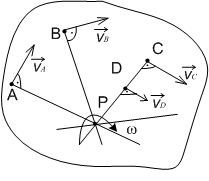
Рис 2.24 Рис.2.25
т.е. угловая скорость плоской фигуры равна отношению скорости какой-либо точки длины отрезка, соединяющего точку с мгновенным центром скоростей, а модули скоростей точек плоской фигуры в любой момент времени пропорциональны длинам отрезков, соединяющих эти точки с мгновенным центром скоростей. Мгновенный центр скоростей, разумеется, может лежать вне плоской фигуры. Но и в этом случае считается, что он в собственности фигуре, полагая размеры фигуры неограниченными.
Разглядим методы нахождения мгновенного центра скоростей плоской фигуры:
1. Заданы скорость какой-либо точки фигуры и ее угловая скорость. Мгновенный центр скоростей Р будет отыскан, в случае, если совершить луч, перпендикулярный скорости , в направлении вращения фигуры и отложить на этом луче отрезок (см. рис. 2.24).
2. В случае, если известны направления скоростей двух точек плоской фигуры и , причем скорость точки А не параллельна скорости точки В, то мгновенный центр скоростей находится на пересечении перпендикуляров к скоростям этих точек (рис. 2.26).
3. В случае, если точка А и В лежат на неспециализированном перпендикуляре к скоростям и этих точек, скорости точек параллельны, то мгновенный центр скоростей Р находится на пересечении прямой и общего перпендикуляра, соединяющей финиши векторов и , так как скорости точек плоской фигуры пропорциональны расстояниям этих точек до мгновенного центра скоростей (рис. 2.27 и 2.28).
В случае, если скорости точек А и В равны между собой ( ) и перпендикулярны отрезку АВ (рис. 2.29), то мгновенный центр скоростей находится в бесконечности ( ; угловая скорость фигуры тело совершает мгновенное поступательное перемещение.
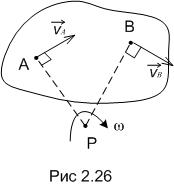
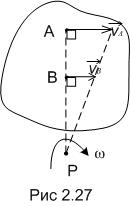
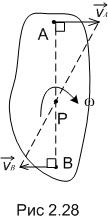
Рис.2.26 Рис.2.27 Рис.2.28
4. Заданы направления скоростей двух точек А и В плоской фигуры, причем скорости эти параллельны друг другу, но не перпендикулярны отрезку АВ (рис. 2.30). Проводя перпендикуляры к заданным направлениям скоростей в точках А и В, находим, что мгновенный центр скоростей лежит в бесконечности . В случае, если угловая скорость фигуры то тело совершает мгновенное поступательное перемещение; скорость всех его точек сейчас времени равны между собой .
5. В случае, если тело катится без скольжения по поверхности неподвижного основания (рис. 2.31), то точка Р основания поверхностей и соприкосновения тела есть мгновенным центром скоростей, потому, что точки контакта имеют однообразную скорость.
2.3.6. Ускорения точек тела при плоском перемещении
Зависимость между ускорениями точек плоской фигуры определяется следующей теоремой:
Ускорение любой точки плоской фигуры равняется геометрической сумме ускорения и ускорения полюса данной точки во вращательном перемещении около полюса.
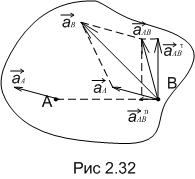Пускай известно ускорение некоей точки А и алгебраические размеры угловой скорости и углового ускорения плоской фигуры. Определим ускорение любой точки В фигуры, приняв точку А за полюс (рис. 2.32).
На основании теоремы о скоростях точек плоской фигуры имеем
(2.61)
где .
Ускорение точки В определяется из выражения
Так как
то имеем
где – касательное ускорение точки В во вращении около полюса А; – обычное ускорение точки В во вращении около полюса А.
Модули этих векторов определяются по формулам
(2.63)
Полное ускорение точки В во вращении около полюса А
(2.64)
равняется по модулю
(2.65)
и направлено под углом ? к отрезку АВ
Совсем, в соответствии с уравнению (2.28), возьмём
(2.67)
2.3.7. Мгновенный центр ускорения
Мгновенным центром ускорений именуется точка плоской фигуры, ускорение которой сейчас времени равняется нулю. Обозначим ее Q.
Для построения мгновенного центра ускорений должны быть известны ускорение одной из точек , угловая скорость ? и угловое ускорение ?, причем предполагается, что ? и ? не равны нулю в один момент. Пускай (рис. 2.33). Из точки А откладываем под углом ? к ускорению отрезок прямой AQ:
Наряду с этим угол ? откладываем от в направлении дуговой стрелки углового ускорения ?, т.е. в разглядываемом случае по часовой стрелке.
В случае, если мгновенный центр ускорения известен, то, выбрав его за полюс, для ускорения точки А плоской фигуры приобретаем
и, следовательно,
Ускорение направлено под углом ? к отрезку AQ, соединяющему точку А с мгновенным центром ускорений в сторону дуговой стрелки углового ускорения ? (рис. 2.34).
Для точки В подобно
и ускорение кроме этого направлено под углом ? к отрезку BQ.
В соответствии с формулам (2.69) и (2.70) имеем
| Рис.2.33 |
т.е. ускорения точек плоской фигуры пропорциональны расстояниям этих точек до мгновенного центра ускорений.
Лекция 2.4. Неспециализированный случай перемещения свободного жёсткого тела
Установлено, что всякое перемещение свободного жёсткого тела из одного положения в второе возможно осуществить совокупностью двух перемещений: поступательного вместе с точкой, принятой за полюс, и поворота тела около оси, проходящей через полюс.