§ 2. предположения и Исходные принципы
Главные общенаучные идеи, лежащие в базе ФА, достаточно несложны и смогут быть, согласно точки зрения П. Благуша (1989), сформулированы так:
а) “сущность вещей заключена в их несложных и вместе с тем многообразных проявлениях, каковые смогут быть растолкованы посредством комбинации нескольких главных факторов”, т.е. за замечаемой вариацией большого количества переменных стоит ограниченное число факторов;
б) “неспециализированную сущность замечаемых вещей мы постигаем, совершая нескончаемые приближения к ней”, т.е. поиск факторов — это долгий процесс познания при помощи перехода к факторам все более большого порядка.
Первым фундаментальным формально-математическим принципом, лежащим в базе хорошей модели ФА1, есть постулат о линейной зависимости между психотерапевтическими чертями (замечаемыми переменными), благодаря которым оценивается какой-либо объект. Количественно степень данной зависимости (связи) возможно оценена посредством коэффициента корреляции. Второе главное предположение пребывает в том, что эти замечаемые переменные (предполагается, что их заведомо избыточное количество) смогут быть представлены как линейная комбинация некоторых латентных переменных либо факторов. Надеется, что последовательность этих факторов являются неспециализированными для нескольких переменных, а другие, характерные факторы, своеобразным образом связаны лишь с одной переменной. Потому, что последние ортогональны друг к другу, то, в отличие от общих факторов, они не вносят вклад в корреляцию (ковариацию)2между переменными. Так, математическая модель ФА сходна с простым уравнением множественной регрессии:
Vi = Ai,1F1 + Ai,2F2 + … + Ai,kFk+ U, (1)
где
Vi — значение i-й переменной, которое выражено в виде линейной комбинации k неспециализированных факторов, Ai,k— регрессионные коэффициенты, показывающие вкладкаждого из k факторов в данную переменную; F1…k— факторы, неспециализированные для всех переменных; U — фактор, характерный лишь для переменной Vi .
Уравнение (1) высказывает очень несложный суть: любая переменная возможно представлена в виде суммы вкладов каждого из неспециализированных факторов. Иначе, подобным образом, любой из k факторов выражается в виде линейной комбинации замечаемых переменных:
Fj = Wj,1*V1+ Wj,2*V2+ … +Wj,p*Vp, (2)
где Wj,i— нагрузки j-го фактора на i-ю переменную либо факторные нагрузки; p — количество переменных.
На рис. 1 факторные нагрузки (w1,1 … w2,6) обозначены разными стрелками, показывающими влияние фактора на конкретную переменную. Переменные v1, v2 и v3 в основном связаны с причиной F1, и лишь фактор F2 имеет маленькую нагрузку на первую переменную; для других трех переменных (v4, v5, v6) неспециализированным причиной есть F2, и только на четвертую переменную F1 имеет малого нагрузку. Эмпирические оценки замечаемых переменных v1 … v6 представлены в столбцах a, b, c, d, e, f, соответственно. Дугообразная стрелка, соединяющая коэффициент и факторы корреляции над ней, подчеркивают факт ортогональности (некоррелированности, линейной независимости) этих факторов, не смотря на то, что в общем случае (об этом ниже) это предположение критично только на этапе выделения начальных факторов, а в будущем, на этапе интерпретации факторного ответа, при вращении факторной структуры допускается возможность корреляции между факторами. (Это один из многих парадоксов ФА, который связан с многозначностью приобретаемого факторного ответа, которое не имеет строго однозначного математического обоснования.)
 |
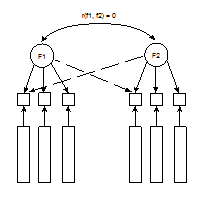Рис.1. Гипотетическая модель с двумя неспециализированными факторами (F1 и F2) и шестью переменными (v1 … v6)
Пользуясь схемой (рис. 1), еще раз обозначим главную задачу ФА: основываясь на эмпирических оценках (a, b, c, d,e, f) исследуемого объекта по каждой из шести переменных-чертей (v1 … v6), исследователь пробует растолковать связь замечаемых переменных влиянием 2-х неспециализированных факторов, в которых находят собственный отражение эти переменные.
§ 3. Главные этапы факторного анализа
На протяжении изучения с применением разведочного ФА возможно выделить три разных этапа: 1) сбор эмпирических данных и подготовка корреляционной (ковариационной) матрицы; 2) выделение начальных (ортогональных) факторов; 3) вращение факторной структуры и содержательная интерпретация результатов ФА. Остановимся на них подробнее.
1. Сбор эмпирических данных в психотерапевтическом изучении разведочного замысла в любой момент опосредован применением какой-либо измерительной процедуры, на протяжении которой испытуемый оценивает измеряемый объект (стимул) по последовательности предложенных исследователем черт. На этом этапе крайне важно, дабы исследователем был предложен большой комплект черт, всесторонне обрисовывающих измеряемый объект. Подбор серьёзных и разнообразных черт и в один момент исключение лишних и несущественных — это достаточно тяжёлое дело, требующее от исследователя опыта, знания литературы и, в известной степени, интуиции. Конкретно продуманный и успешный подбор оцениваемых черт определяет в конечном итоге успех в выделении значительных и значимых факторов, стоящих за ними — это главное, о чем нельзя забывать на данном этапе. В противном случае говоря, из случайного комплекта черт объекта нереально выделить такие факторы, каковые будут закономерно и содержательно определять его оценку испытуемыми. Ясно, что с первого раза, априорно не редкость тяжело подобрать необходимые характеристики. Исходя из этого еще раз отметим, что разведочное изучение посредством ФА — это долгий и интеративный процесс, в то время, когда результаты прошлого анализа разрешают оценить допущенные неточности и скорректировать процедуру последующего изучения.
Второе значительное замечание появляется в связи с постулатом линейности. При, в то время, когда связь между психотерапевтическими чертями выясняется значительно нелинейной, базовая размерность искомого факторного пространства возрастает, и это ведет к фальшивому ответу. Преодоление данной трудности может идти двумя дорогами. Во-первых, возможно применять коэффициент криволинейной корреляции (по Пирсону, к примеру), а во-вторых, направляться избегать тех психотерапевтических переменных, каковые имеют между собой очевидно нелинейные связи.
На данном этапе нельзя не коснуться вопроса о нужном уровне измерения, потому, что он первым делом связан с применением конкретного способа измерения. Вычислительные методы ФА требуют, дабы измерения замечаемых переменных были совершены не ниже, чем по шкале промежутков. Это требование, к сожалению, выполняется далеко не всегда, что, но, связано не столько с неосведомленностью исследователя, сколько с ограниченностью выбора измерительного способа и/либо его адекватностью конкретной задаче либо кроме того процедуре изучения. Реалии практики применения ФА в психологии таковы, что в подавляющем большинстве работ используется один из вариантов способа балльной оценки, что, как мы знаем, дает шкалу порядка. Налицо явное ограничение в применении ФА. При ответе данной неприятности направляться иметь в виду следующее. Во-первых, стоит выделить большое внимание проработке процедурных моментов в применении способа балльной оценки, дабы выйти за установление лишь порядковых взаимоотношений и максимально “приблизиться” к шкале промежутков. Во-вторых, направляться не забывать, что математическая процедура ФА оказывается достаточно устойчивой к разнообразные измерительным некорректностям при оценке коэффициентов корреляции между переменными. И наконец, в самой математической статистике существуют разные подходы к ответу данной неприятности (Дж. Ким, Ч. Мьюллер,1989), и для более качественной (не строго метрической) трактовки результатов ФА указанное ограничение получает не через чур принципиальное значение.
Достаточно серьёзен вопрос о количестве применяемых переменных либо, более операционально, о том, сколько переменных должно приходиться на один гипотетический фактор. За Терстоуном многие авторы уверены в том, что в разведочном ФА на один фактор должно приходиться как минимум несколько переменных. Для конфирматорного ФА эта пропорция меньше и, в большинстве случаев, исследователи ограничиваются двумя переменными. В случае, если исследователя интересует оценка надежности приобретаемых факторных нагрузок, существуют и более строгие оценки количества нужных переменных (Дж. Ким, Ч. Мьюллер, 1989).
Формальный результат первого этапа — получение матрицы смешения и на ее базе — корреляционной матрицы. Матрица смешения — это таблица, куда заносятся результаты измерения замечаемых переменных: в столбцах матрицы (по числу переменных) представлены оценки испытуемых (либо одного испытуемого) каждой из переменной; строки матрицы — это разные наблюдения каждой переменной. В случае, если задача исследователя — выстроить факторное пространство для одного испытуемого, то необходимо обеспечить множественность таких наблюдений (к примеру, повторить их пара раз). В том случае, в то время, когда строится групповое факторное пространство, достаточно взять по одной оценке от каждого испытуемого. Для расчета согласно этой информации корреляционной матрицы с достаточно точными коэффициентами корреляции направляться обеспечить нужное число наблюдений, т.е. количество строчков в матрице смешения. В большинстве случаев не нужно планировать менее 11—12 наблюдений.
Корреляционная матрица (матрица попарных корреляций между переменными) рассчитывается, в большинстве случаев, с применением коэффициента линейной корреляции Пирсона. Довольно часто появляется вопрос о правомерности и возможности применять другие меры сходства (сопряженнности) между переменными, основанные на ранговой (порядковой) статистике. Ясно, что этот вопрос появляется в любой момент, в то время, когда исследователь трудится с номинальными либо порядковыми данными. В строгом смысле ответ будет отрицательным. Но направляться учесть два мысли. Во-первых, продемонстрировано, что при достаточном числе наблюдений коэффициент линейной корреляции Пирсона достаточно устойчив к применению при расчетах результатов порядковых измерений. Во-вторых, как было отмечено выше, в случае, если перед исследователем стоит задача не столько количественного, сколько качественного анализа данных, то такое эвристическое применение ФА считается в полной мере оправданным.
Еще один узкий вопрос, который связан с построением матрицы попарных корреляций связан с тем, какую матрицу применять в ФА — корреляционную либо ковариационную? Для начала напомним соответствующие формулы.
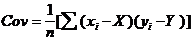Коэффициент ковариации
(3)
между двумя переменными x и y, а коэффициент корреляции:
rxy = Cov/sxsy , (4)
где n — количество наблюдений; xi и yi — значения переменных x и y ;X и Y — средние арифметические значения переменных x и y по последовательности наблюдений; sx и sy — средние квадратические отклонения переменных x и y по последовательности наблюдений.
Так разумеется, что коэффициент корреляции — это тот же коэффициент ковариации, лишь нормированный по среднему квадратическому отклонению либо, как еще говорят, выраженный в единицах среднего квадратического отклонения переменных. Из этого следуют и “рецепты” по применению в ФА корреляционной либо ковариационной матриц:
1) в случае, если все переменные выражены в одних и тех же единицах измерения, то нет громадного различия, какую из матриц факторизовать;
2) в случае, если метрики переменных заметно отличаются (единицы измерения существенно неоднородны и дисперсии переменных заметно отличаются), то целесообразно применять анализ корреляционной матрицы;
3) ковариационные матрицы предпочтительнее, в то время, когда нужно совершить сравнение результатов ФА (факторных структур) в двух разных выборках, взятых в одном и том же изучении, к примеру, в то время, когда требуется оценить повторяемость какого-либо занимательного результата.
2. Следующий наиболее значимый этап ФА — фактически факторизация матрицы корреляций (ковариаций) либо выделение начальных (ортогональных) факторов. На данный момент — это абсолютно компьютеризованная процедура, которую возможно отыскать во всех современных статистических программах. Одним из первых, кто внес предложение формально-математическое решение проблемы возможности факторизации корреляционной матрицы, был Л. Терстоун. В матричной форме его известное уравнение выглядит следующим образом (подробнее см.: Я. Окунь, 1974, c. 43—49):
(5)
где — редуцированная корреляционная матрица;
— редуцированная матрица факторных нагрузок;
— транспонированная матрица факторных нагрузок.
Поясним, что редуцированная корреляционная матрица — это матрица попарных корреляций замечаемых переменных, где на основной диагонали лежат не единицы (как в полной матрице корреляций), а значения, соответствующие влиянию лишь неспециализированных для этих переменных факторов и именуемые общностями. Подобным образом, редуцированная матрица факторных нагрузок либо факторная матрица (формальная цель ФА) представляет собой факторные нагрузки лишь неспециализированных факторов.
Главная неприятность, стоящая при ответе уравнения (3), содержится в том, что значения общностей в редуцированной корреляционной матрице малоизвестны, а для начала вычислений их нужно иметь. На первый взгляд неразрешимая неприятность решается так: до начала вычислений задаются кое-какие приблизительные значения общностей (к примеру, большой коэффициент корреляции по столбцу), а после этого на последующих стадиях вычислений, в то время, когда уже имеются предварительные размеры вычисленных факторных нагрузок, они уточняются. Так, разумеется, что вычислительные методы ФА являются последовательностью итеративных1вычислений, где результаты каждого последующего шага определяются результатами прошлых. С известной долей упрощения можно считать, что разные методы факторизации корреляционной матрицы по большей части и отличаются тем, как конкретно решается эта неприятность.
Для людей, неискушенных в проблемах математической статистики, но решающих посредством ФА собственную задачу, более серьёзен главный суть процедуры факторизации, заключающийся в переходах от матрицы смешения к корреляционной матрице и потом к матрице факторных нагрузок и построению факторных диаграмм (рис. 2).
 |
|||
 |
Рис. 2. Главные этапы изменения данных на протяжении факторного анализа.
Пользуясь данным рисунком, еще раз выделим ответственную изюминку ФА — это метод понижения размерности, сжатия количества данных. Обратите внимание, что исходная матрица смешения достаточно, громадна, к примеру, при условии 20-ти наблюдений каждой переменной она содержит 20Њ?6=120 измерений. Конечный итог анализа — это всего лишь 2?6=12 чисел либо выстроенная по матрице факторных нагрузок компактная факторная диаграмма. Так, при адекватном применении ФА как способа многомерного измерения мы можем взять 10-кратную компрессию исходной информации и наглядность результатов ее анализа.
Отметим, что основная цель выделения первичных факторов в разведочном ФА пребывает в определении предельного количества неспециализированных факторов, каковые удовлетворительно воспроизводят (растолковывают) корреляции между замечаемыми переменными. Главная стратегия при выделении факторов незначительно отличается в различных способах. Она содержится в оценке догадки о минимальном числе неспециализированных факторов, каковые оптимально воспроизводят имеющиеся корреляции. В случае, если нет каких-либо догадок о числе факторов (в ряде программ оно возможно задано прямо), то начинают с однофакторной модели. Эта догадка о достаточности одного фактора оценивается посредством применяемого критерия оптимальности соответствия данной однофакторной модели исходной корреляционной матрице. В случае, если расхождение статистически значимо, то на следующем шаге оценивается модель с двумя факторами и т. д. Таковой процесс подгонки модели под эти осуществляется , пока с позиций применяемого критерия соответствия расхождение не станет минимальным и будет оцениваться как случайное. В современных компьютерных статистических программах употребляются разные способы факторизации корреляционной матрицы. Нам представляется, что, не смотря на то, что для исследователя эта неприятность не воображает прямого интереса, однако она ответственна, потому, что от выбора способа факторизации в определенной мере зависят результаты расчета факторных нагрузок. В силу специфики отечественного изложения баз ФА мы ограничимся только перечислением этих способов, снабдив его весьма краткими комментариями и отошлем читателя для более глубокого знакомства к особой литературе, требующей некоторых познаний в математике (Дж. Ким, Ч. Мьюллер, 1989):
Способ основных факторов (либо основных осей) — самый старый и довольно часто применяемый в разных предметных областях.
Способ мельчайших квадратов сводится к минимизации остаточной корреляции по окончании выделения определенного числа факторов и к оценке качества соответствия вычисленных и замечаемых коэффициентов корреляции по критерию минимума суммы квадратов отклонений.
Способ большого правдоподобия: специфика данного способа пребывает в том, что при громадной выборки (громадного количества наблюдений каждой переменной) он дает возможность приобрести статистический критерий значимости взятого факторного ответа.
Альфа-факторный анализ был создан специально для анализа психотерапевтических данных, и исходя из этого его выводы носят по большей части психометрический, а не статистический темперамент. В альфа-факторном анализе предельное число неспециализированных факторов оценивается по размерам собственных коэффициентов обобщенности и значений факторов a, каковые должны быть больше 1 и 0, соответственно.
Факторизация образов (либо анализ образов). В отличие от хорошего ФА в анализе образов предполагается, что общность каждой переменной определяется не как функция гипотетических факторов, а как линейная регрессия всех остальных переменных.
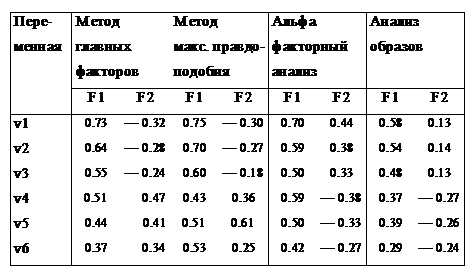
В табл. 1 представлены сравнительные результаты факторизации корреляционной матрицы (Дж. Ким, Ч. Мьюллер, 1989, с. 10), с применением 4-х разных способов. Видно, что полученные результаты смогут различаться, даже если не обращать внимание на символы факторных нагрузок (об этом чуть ниже).
Таблица 1
Применение разных способов факторизации для получения двухфакторного решения
 |
По окончании компьютерного расчета матрицы факторных нагрузок наступает самый сложный, важный и творческий этап применения ФА — определение предельного количества факторов, адекватно воспроизводящих замечаемые корреляции, и содержательная интерпретация результатов ФА. Отметим, что предельное число факторов равно переменных. Не считая содержательных параметров решения вопроса о минимальном числе факторов существуют формально-статистические показатели достаточности числа выделенных факторов для объяснения корреляционной матрицы. Остановимся на двух главных показателях. По окончании расчета факторных нагрузок для каждой переменной фактически каждая компьютерная программа распечатывает на экране следующую табл. 2.
Первый ответственный показатель в данной таблице (второй столбец) — это величина собственного значения каждого фактора; факторы находятся в таблице по убыванию данной величины. Не весьма строго говоря, данный показатель характеризует вес, значимость каждого фактора в отысканном факторном ответе2. Из таблицы 2 видно, что от 1-го фактора к 10-му (всего было 10 переменных) величина собственного значения убывает более, чем в 100 раз. Конечно появляется вопрос о том, какая величина данного показателя говорит о значимом, значительном вкладе соответствующего фактора, и каков критерий для отсечения незначимых, несущественных факторов. Достаточно довольно часто в качестве для того чтобы критического значения применяют величину собственного значения, равную 1.0. Так, с определенной степенью уверенности предполагают, что те факторы, у которых данный показатель меньше 1.0, не вносят большого вклада в объяснение корреляционной матрицы. Не считая анализа табличных размеров не редкость полезно визуально оценить динамику величины собственного значения по графику. В большинстве случаев, в большинстве статистических программ такая возможность пользователю предоставляется (см. рис. 3). Как предлагал в свое время Р. Кеттел (1965), выделение факторов заканчивается, в то время, когда по окончании падения величины собственного значения изменяются незначительно, и график практически преобразовывается в горизонтальную прямую линию. Не обращая внимания на видимую ясность и простоту для того чтобы рецепта, направляться подчернуть, что в то время, когда на графике имеется более чем один излом, то выделение горизонтального участка делается неоднозначным.
Таблица 2
Статистические показатели для определения предельного числа факторов
 |
|||
 |
Рис. 3. Изменение величины собственного значения факторов: ось абсцисс — количество факторов; ось ординат — величина собственного значения
Второй не меньше ответственный расчетный показатель значимости каждого фактора — процент растолковываемой дисперсии переменных, содержащейся в корреляционной матрице (третий столбец в табл. 2). Конечно, что все 100% дисперсии будут разъясняться лишь всеми десятью факторами. Но не следует забывать, что при любых измерениях (а особенно в разведочных, пилотажных изучениях) имеют место разнообразные случайные неточности, и исходя из этого их вклад в неспециализированную дисперсию также может оказаться очень большим. Предполагается, что последовательность выделенных факторов отражает влияние случайных процессов, никак не связанных с оценкой замечаемых переменных. Так, формально задача содержится в том, дабы, с одной стороны, выбрать некое предельное число факторов, каковые бы, иначе, растолковывали большой процент всей дисперсии переменных. Ясно, что эти два требования в принципе взаимно противоречивы, и, следовательно, исследователь стоит перед выбором некоей критической величины процента растолковываемой дисперсии. К сожалению, никаких строго формальных рецептов по этому поводу не существует, но принято вычислять, что при хорошем факторном ответе выбирают столько факторов, дабы они в сумме (последний столбец таблицы) растолковывали не меньше 70—75%. В отлично спланированных изучениях с установленной факторной структурой данный суммарный процент может быть около 85—90 %.
Подводя результат, укажем, что в этом случае оба статистических критерия в полной мере конкретно говорят о достаточности не более 3-х факторов, что и отмечено пунктирной горизонтальной линией. Однако, стоит выделить, что главным критерием для выделения предельного числа будет содержательная интерпретация выделенных факторов, а к применению формально-статистических параметров направляться относиться с осторожностью.
3. Вращение факторной структуры и содержательная интерпретация результатов ФА. Одним из главных кажущихся парадоксов ФА как способа, обеспеченного очень солидным и современным математическим аппаратом, есть неоднозначность расчета факторных нагрузок по исходной корреляционной матрице. Практически это указывает следующее: любой метод факторизации корреляционной матрицы дает какой-то один вариант расчета факторных нагрузок из целого множества эквивалентных. Это указывает, что расчет факторных нагрузок выполняется с точностью до любого линейного преобразования в правой части уравнения (2), что эквивалентно возможности произвольного поворота факторных осей около векторов-переменных. Поясним сообщённое, применяя геометрическую интерпретацию результатов ФА. На рис. 4 представлены три переменные (v1, v2 и v3) в пространстве двух ортогональных факторов (F1 и F2). Переменные изображены в виде векторов, а факторные нагрузки переменных на факторы геометрически представляют собой проекции данного вектора (переменной) на соответствующую координатную ось (фактор). В случае, если мы осуществим произвольный поворот осей координат на какой-то угол, к примеру, на 45 градусов вправо (новые оси — штрих-пунктирные линии на рис. 4), то размещение переменных в новой совокупности координат (F1′ — F2′) с математической точки зрения абсолютно эквивалентно исходному. Изменились только величины факторных нагрузок (сравните проекции переменной v1 на оси F1 и F1′, соответственно, до и по окончании поворота).Так, исходное факторное ответ справедливо с точностью до любого угла поворота ортогональных факторных осей около пучка векторов, образованного переменными v1, v2 и v3.
 |
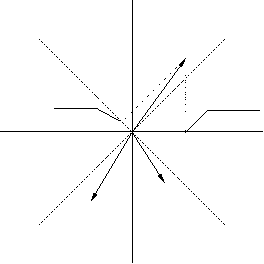Рис.4. Факторное пространство 3-х переменных (v1, v2 и v3) в пространстве 2-х факторов: целые линии (F1, F2) — до поворота; пунктирные линии (F1′, F2′) — по окончании поворота
Конечно, появляется вопрос об оптимальном размещении переменных в пространстве факторных осей. Как было отмечено выше, эта неприятность в принципе не имеет строгого математического ответа. Она относится уже к содержательной интерпретации размещения переменных в факторном пространстве. Практически сущность неприятности пребывает в следующем: какой комплект факторных нагрузок (либо какая геометрическая модель результатов ФА) будет более подходящим для интерпретации исследователем. Потому, что при повороте осей координат факторные нагрузки по одному фактору смогут расти, а По другому — уменьшаться, то, соответственно, будет расти либо уменьшаться вклад этих факторов в различные переменные. Из этого направляться, что необходимо искать таковой вариант размещения переменных в факторном пространстве, что наилучшим образом соответствует ожиданиям исследователя, его версиям о взаимозависимости и взаимосвязи исследуемых переменных. В большинстве случаев, при применении ФА считают, что существует одно оптимальное положение осей координат, соответствующее значительным для данного изучения и отлично трактуемым факторам.
Обрисованный выше процесс поиска оптимальной факторной структуры стал называться процедуры вращения факторов. По образному выражению Л. Терстоуна, цель исследователя содержится в поиске “несложной структуры” либо попытке растолковать большее число переменных меньшим числом факторов. С формальной точки зрения при поиске несложной структуры направляться иметь в виду следующее: целесообразно стремиться к получению для каждой переменной предельного количества громадных факторных нагрузок по одним факторам и одновременно наибольшего количества минимальных факторных нагрузок по вторым факторам. Следуя этому правилу, мы стремимся сделать так, дабы одну группу переменных возможно было в основном растолковать влиянием одних факторов, а другую — вторых. Так, “простота” хорошего факторного ответа содержится в том, что любая переменная имеет самый простое факторное объяснение, т.е. характеризуется преобладающим влиянием некоего одного фактора, и в меньшей степени связана с другими факторами. И напротив: один фактор должен быть своеобразным образом связан с одной группой переменных и не связан с другими переменными. В предельном случае самая несложная структура получается тогда, в то время, когда все переменные находятся на соответствующих факторных осях, т. е. имеют ненулевые факторные нагрузки лишь по одному фактору, а по остальным — нулевые. Возвращаясь к рис. 4, укажем на итог вращения: по окончании поворота факторных осей на 45 градусов вправо, нагрузка переменной v1 по первому фактору быстро уменьшилась и в один момент мало возросла по второму. Помимо этого заметно уменьшились факторные нагрузки переменных v2 и v3 по второму фактору. Так “простота” новой факторной структуры выразилась в главном влиянии первого фактора на переменную v1, а второго фактора — на две вторых переменных.