Вопросы по курсу «ЛОГИКА» (зачет)
1. Предмет логики как науки. Логическая форма (структура) мысли.
2. Формализация как средство обнаружения логической формы.
3. язык и Общая характеристика логики высказываний.
4. Неточности в мышлении. Их классификация.
5. Понятие «высказывание». Виды высказываний. Язык логики высказываний.
6. Виды сложных высказываний. Значение логических альянсов.
7. Табличный метод определения логических законов.
8. Элементарные законы логики: закон тождества, закон несоответствия, закон исключенного третьего.
9. Логическая черта имени: содержание и объём.
10. Содержание имени. Виды имен по содержанию (собирательные/ несобирательные, абстрактные/ конкретные, хорошие/ отрицательные, относительные/ безотносительные).
11. Количество имени. Виды имен по количеству.
12. Отношения между именами. Круги Эйлера как средство анализа взаимоотношений между количествами имен.
13. обобщение и Ограничение имени.
14. Деление как логическая операция. Структура деления.
15. Виды деления (логическое, аналитическое).
16. Правила логического деления. Неточности при делении.
17. Определение как логическая операция. Структура определения.
18. Правила определения и вероятные неточности при их нарушении.
19. виды и Структура атрибутивных высказываний.
20. Распределенность терминов в атрибутивных высказываниях.
21. Отношения между атрибутивными высказываниями. Логический квадрат.
22. Яркие силлогистические выводы: превращение (обверсия), обращение (конверсия), противопоставление предикату (частичная контрапозиция).
23. Главное правило ярких силлогистических выводов.
24. Структура несложного окончательного силлогизма.
25. Неспециализированные правила несложного окончательного силлогизма.
26. Фигуры несложного окончательного их правила и силлогизма.
27. Энтимема. Процедура восстановления энтимемы до полного силлогизма.
28. Аргументация: её структура, правила и виды.
29. Неточности в аргументации.
30. Логические требования к созданию научного текста.
Составитель: доцент кафедры
философии культуры, к.ф.н., доцент Малая Н.В.
ЛОГИКА. Предмет логики как науки
Логическая схема – это та её сторона, которая не зависит от конкретного содержания, но помогает для связи, преобразования и упорядочения его элементов.
Виды логических схем. Рассуждения верные, рискованные и абсурдные.
Логический закон-схема, которая при любом содержании принимает лишь подлинные значения, а соответствующее ей рассуждение – верное.
Выполнимая схема — логическая схема, которая при одних подстановках преобразуется в подлинные, а при вторых в фальшивые выражения, а соответствующее ему рассуждение – рискованное.
Противоречивая схема — логическая схема, которая при любой подстановке преобразуется в фальшивые выражения, а соответствующее ему рассуждение — абсурдное.
истинности и Соотношение правильности
Идея подлинна, если она соответствует действительности. Правильность характеризует идея с позиций внутренней связи между её элементами. Соблюдение правильности при подлинных данных постоянно ведёт к подлинным итогам.
Познавательные неточности в рассуждениях
Познавательные неточности, которые связаны с неверными представлениями о настоящем положении дел, именуются содержательными.
Неточности, которые связаны с нарушениями правильности мышления, именуются формальными, либо логическими. Они делятся на софизмы и паралогизмы.
Паралогизм – это непреднамеренная логическая погрешность. Софизм – преднамеренное нарушение требований логики, прием интеллектуального мошенничества, который связан с попыткой выдать неправда за истину, либо напротив.
РАЗДЕЛ 1. ВЫСКАЗЫВАНИЯ
Неспециализированная черта логики высказываний
Высказывание — языковое выражение, о котором возможно сообщить лишь одно из двух: действительно оно либо ложно.
Высказывания (как и соответствующие им схемы построения) делятся на простые и сложные. Сложное высказывание возможно разбить на простые. Простое высказывание на более простые не расчленяется. При построении схем в качестве переменных для несложных высказываний в большинстве случаев употребляются строчные буквы латинского алфавита: p,q,r,s,…; для любых же (время от времени нам безразлично, простое это высказывание либо сложное) — прописные буквы этого алфавита: A,B,C,D, …
Схема высказывания принимает логическое значение – «действительно» либо «ложно».
Логическое значение сложной схемы высказывания в современной логике ставится в зависимость (есть функцией) от логических значений несложных схем.
Определения наиболее значимых схем логики высказываний
Сложные высказывания и соответствующие им схемы образуются посредством особенных выражений, каковые именуются функторами (отрицание, конъюнкция, дизъюнкция (не сильный и сильная), импликация, эквиваленция). Сложную схему принято именовать именем функтора, благодаря которому оно образовано, т.е. в случае, если, к примеру, схема образуется посредством конъюнкции, то и сама она именуется конъюнкцией.
Отрицанием A именуется схема, обозначаемая выражением OA (читается: «не-A», «неверно, что A»), которая принимает значение «действительно», в случае, если и лишь в случае, если A принимает значение «ложно». Данное определение возможно выразить посредством следующей таблицы (таблицы истинности), где «и» обозначает «действительно», а «л» – «ложно»:
Таблица 1
| A | O A |
| и | л |
| л | и |
Конъюнкция A и B — схема, обозначаемая выражением AUB, которая принимает значение «действительно», в случае, если и лишь в случае, если значение «действительно» принимает как A, так и B (см. 3-й столбец табл. 2). Выражение A U B читается: «светло синий и B».
Таблица 2
| A | B | A U B | A U B | A U B | A ® B | A « B |
| и | и | и | и | л | и | и |
| л | и | л | и | и | и | л |
| и | л | л | и | и | л | л |
| л | л | л | л | л | и | и |
Дизъюнкция не сильный А и В — схема, обозначаемая выражением AUB, которая принимает значение «действительно», в случае, если и лишь в случае, если значение «действительно» принимает хотя бы одно из A и B (см. 4-й столбец табл. 2). Выражение AUB читается: «A либо B».
Дизъюнкциия сильная А и В — схема, обозначаемая выражением AUB, которая принимает значение «действительно», в случае, если и лишь в случае, если значение «действительно» принимает только одно из A и B (см. столбец 5-й табл. 2). Выражение AUB читается: «или A, или B».
Импликация A и B — схема, обозначаемая выражением A®B, которая принимает значение «ложно», в случае, если и лишь в случае, если A принимает значение «действительно», а B – значение «ложно» (см. 6-й столбец не. 2). Выражение A®B читается: «В случае, если A, то B».
Эквиваленция A и B – схема, обозначаемая выражением A«B, которая принимает значение «действительно», в случае, если и лишь в случае, если логические значения A и B совпадают (см. 7-й столбец табл. 2). Выражение A«B читается: «A тогда и лишь тогда, в то время, когда B».
Алфавит логики высказываний включает знаки:
1.p, q, r, s, … – знаки, каковые обозначают переменные для несложных высказываний; A, B, C, D, … — знаки, каковые обозначают переменные для любых высказываний;
2.U, U, U, ®, «, O — знаки для обозначения логических альянсов;
3.(, ) – скобки как указатели совершения логических действий.
Никаких вторых знаков в логике высказываний нет.
Осмысленное выражение языка логики высказываний определяется следующим образом:
1.Любая переменная имеется осмысленное выражение;
2.В случае, если А – осмысленное выражение, то OA, A U B, A U B, A U B, A®B, A«B — также осмысленные выражения;
3.Никаких вторых осмысленных выражений в логике высказываний нет.
Законы логики высказываний
Для обнаружения форм, являющихся логическими законами, возможно воспользоваться таблицами истинности. Схема, порождающая лишь подлинные сложные высказывания, есть ЛОГИЧЕСКИМ ЗАКОНОМ.
самые простыми законами логики высказываний являются законы, каковые возможно выразить посредством одной переменной – закон исключенного третьего, закон несоответствия, закон тождества, закон удаления двойного отрицания, введения двойного отрицания и др.
Закон исключенного третьего– схема AUOA – два отрицающих друг друга высказывания не являются совместно фальшивыми, выполняется одна из возможностей: в случае, если ложно одно из этих высказываний, то действительно его отрицание, а что-либо третье исключено.
Закон несоответствия — схема O(AU OA) — два отрицающих друг друга высказывания не являются совместно подлинными, одно их них ложно.
Закон тождества – схема A«A – всякое высказывание есть эквивалентным (тождественным) самому себе, следовательно, в верном рассуждении оно согласуется с самим собой.
Закон удаления двойного отрицания– схема OOA®A — отрицание два раза некоего высказывание образует его утверждение.
Закон введения двойного отрицания– схема A ® OOA-утверждение некоего высказывание образует его двойное отрицание. Справедливость рассмотренных законов с одной переменной легко проверяется табличным методом (см. таблицу 5).
Таблица 5
| A | A U OA | O(A U OA) | A « A | OOA ® A | A ® OOA |
| и | и | и л | и | и | и |
| л | и | и л | и | и | и |
РАЗДЕЛ 2. ИМЕНА
Главные характеристики имени
Имя — выражение языка, обозначающеё отдельный предмет либо множество, совокупность предметов.
Множество (совокупность, класс) предметов, обозначаемых именем, именуется количеством имени. Отдельные предметы, входящие в количество имени, именуются элементами количества имени. Подклассы количества имени именуются частями количества.
Содержание имени- совокупность показателей тех предметов, каковые обозначаются данным именем. Под показателем понимается любое свойство, каждая черта предмета.
Показатели, составляющие содержание имени, смогут быть родовыми, видовыми и личными. В случае, если мы в пределах какого-либо достаточно широкого класса объектов выделяем более узкий класс объектов, то показатели, выделяющие более широкий класс, будут принимать во внимание родовыми, а показатели, выделяющие более узкий класс, — видовыми. Личными показателями являются такие, каковые конкретно выделяют этот единичный объект.
Главным содержанием имени возможно именовать ту минимальную часть его содержания, из которого в той теории, к которой относится имя, логически выводимо все другое содержание имени (которое при таких условиях именуется производным). Совокупность же главного и производного содержаний имени есть его полным содержанием.
ВИДЫ ИМЕН
В случае, если в количество имени входит лишь один предмет, то такое имя именуют единичным.
Неспециализированное имя — это имя, в количество которого входит более одного элемента. Класс, являющийся количеством неспециализированного имени, именуют значением этого имени.
Особенной разновидностью неспециализированных имен являются универсальные имена, либо универсумы. Ими фиксируются все классы объектов, все элементы, исследуемые в той либо другой области познания. Имена, входящие в одинаковый универсум, именуются родственными.
Нулевые (безлюдные) имена в самом неспециализированном виде определяются как имена, количество которых не содержит ни одного элемента. Класс, не содержащий ни одного элемента, именуют нулевым, либо безлюдным.
Различают кроме этого имена описательные и личные. Описательные имена обозначают объекты, показывая их соответствующие показатели. Личные имена обозначают объекты методом яркой соотнесенности с ними, потому, что в культуре людской сообщества сложились определенные традиции, нормы именования.
Принципиально важно различать собирательные и несобирательные имена. Несобирательным именуется такое имя, любой элемент количества которого представляет собой что-то единое, целостное. Собирательным именуется такое имя, любой элемент которого есть совокупностью, собранием, объединением каких-то объектов.
Выделяют хороших и отрицательных имен. Оно базируется на том, что объекты возможно охарактеризовать как по наличию, так и по отсутствию у предметов некоторых особенностей. Хорошим считается имя, в содержании которого указываются свойства, свойственные объектам. Отрицательным считается имя, в содержании которого указываются свойства, отсутствующие у предметов.
Наконец, укажем деление имен на чёткие и нечёткие. В случае, если имя таково, что довольно любого предмета возможно совершенно верно, конкретно решить, входит либо не входит данный предмет в количество данного имени, то это имя именуют четким (правильным, определенным) по количеству (напр., рациональное число, натуральное хозяйство, уголовная ответственность). В другом случае имя считается нечетким (неизвестным, расплывчатым, размытым, неточным) по количеству (напр., дорогой товар, юный человек, приятная наружность).
ОТНОШЕНИЕ СОВМЕСТИМОСТИ
Имена считаются совместимыми в случае, если их количества хотя бы частично совпадают, т.е. эти количества имеют неспециализированные элементы.
Виды совместимых имён:
1) Равнообъёмными (равнозначными) считаются имена, количества которых абсолютно совпадают (рис.1)[1]. При отношении равнообъёмности имен AиB любой предмет, обозначенный именем A,может бытьобозначен именем B, и напротив.
2) Имена находятся в отношении подчинения, в случае, если количество одного абсолютно включается в количество другого, но не сходится с ним. Наряду с этим включающеё имя именуется подчиняющим, либо родовым, а включенное – подчиненным, либо видовым. В случае, если имя A подчиняется имени B (рис.2), то все показатели Bприсущи содержанию имени A, и любой предмет, обозначаемый именем A, может обозначаться именем B (но не наоборот).
3) Пересекающимися (перекрещивающимися) являются такие имена, количества которых только частично входят приятель в приятеля. Наряду с этим кое-какие предметы, обозначаемые именем A, смогут обозначаться именем B, и напротив. В случае, если имена A и B находятся в отношении пересечения (рис.3), то предметы, входящие в один момент в количества имен A и B, другими словами находящиеся на пересечении этих количеств, владеют одними и теми же показателями.
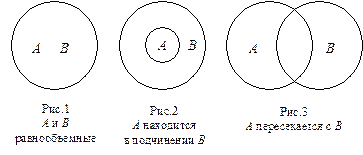
Отношения между родственными именами.
Отношение несовместимости
При отношении несовместимости в содержании одного из имен указываются показатели, исключающие показатели содержания другого имени.
Виды несовместимых имён:
1) Противоречащими именуются два несовместимых имени, видовое содержание одного из которых (т.е. совокупность его видовых показателей) есть отрицанием видового содержания другого. Такие имена абсолютно исчерпывают количество третьего, подчиняющего их имени (рис.4).
2) Внеположенными именуются такие несовместимые имена, количества которых в сумме составляют часть количества некоего подчиняющего (родового) имени. Потому, что A и B, будучи внеположенными, в один момент подчинены С, постольку их именуют кроме этого соподчиненными довольно С (рис. 5).
3) Противоположными именуют имена, содержания которых высказывают какие-либо крайние характеристики в некоем упорядоченном последовательности понемногу изменяющихся особенностей (рис. 6).
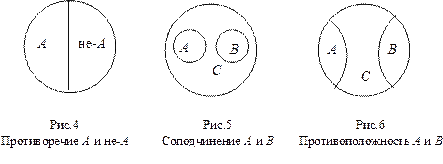
ограничение и Обобщение как операции с именами
Обобщение количества A ? логическая операция, из-за которой образуется имя с количеством B, содержащим в себе количество A. Иными словами, обобщить имя A ? значит образовать такое второе имя B (род), которое подчиняло бы себе имя A (вид). Пределом обобщения в каждом конкретном случае выступает некое универсальное имя.
Ограничение ? логическая операция, обратная обобщению. Она пребывает в нахождении имени с количеством B, что содержится в количестве A. Сократить количество A ? значит отыскать такое второе имя B (вид), которое пребывало бы в отношении подчинения к A (роду). Пределом ограничения выступают имена, количества которых равны одному предмету (единичные имена).
Особенной разновидностью ограничения есть выделение типа, либо типизация. Тип ? это имя, которому однородные предметы соответствуют в той либо другой мере. В случае, если кое-какие предметы составляют количество имени A и среди них имеется такие, что непременно (т.е. со степенью, равной 1) принадлежат к количеству B, а другие владеют этим свойством в некоей (меньшей 1) степени, то имя с количеством B является типом .
Присоединение к количеству А новых предметов, тождественных со ветхими по некоему показателю, именуется логической операцией расширения количества A.
Операция, обратная расширению, т. е. удаление из количества A предметов, каковые тождественны с оставшимися по некоторым показателям, именуется локализацией количества имени A.
Логические операции с количествами имен не нужно смешивать с мысленными переходами от части к целому и, напротив, от целого к части. Специфика последних самый четко выявляется при их сопоставлении с операциями ограничения и обобщения.
ОПЕРАЦИЯ ДЕЛЕНИЯ
Деление логическое– это логическая операция, при помощи которой количество имени (род) распределяется по классам (видам).
Деление аналитическое – это операция, которая связана с мысленным вычленением в целом его частей. Эти операции не нужно смешивать.
Деление возможно хорошим либо неклассическим. При хорошем делении как род, так и виды – имена с четким количеством, при неклассическом они являются нечеткие, расплывчатые имена, либо типы.
Хорошее логическое деление пребывает в нахождении для имени A таких имен A1, A2, …, An (n – конечное число), что:
а) любой из количеств A1, A2, … , An находится в отношении подчинения к количеству A);
б) сумма количеств A1, A2, … , An равна количеству A;
в) любая пара количеств A1, A2, … , An связана отношением несовместимости. Наряду с этим имя A именуется делимым именем, а A1, A2, … , An – участниками деления.
В содержательном замысле деление пребывает в разбиении рода предметов соответственно основанию деления, т.е. изюминкам (вариантам) показателя, свойственного данным предметам.
Быть может, что в качестве основания деления выступает показатель, свойственный только части предметов некоего класса. При таких условиях предметы делятся на те, каковые этим показателем владеют, и те, каковые им не владеют. Такое деление именуется дихотомическим (греч. dicho – на две части, tome – сечение). В отличие от него деление по показателю, которым владеют все предметы рода и что варьируется в видах, именуется политомическим греч. polis– довольно много).
Отличие деления от расчленения базируется на разном характере взаимоотношений целое – род и часть – вид.
ПРАВИЛА ДЕЛЕНИЯ
1. Правило адекватности.Деление должно быть соразмерным. Это указывает, что при деления любой из количеств A1, A2,, … , An должен быть видом количества A, и сумма A1, A2,, … , An обязана исчерпывать целый количество A;при расчленениямысленное соединение частей должно быть равняется целому.Отступление от этого правила ведет к неточностям, самые известные из которых: деление с лишними участниками, в то время, когда некий из количеств (частей) A1, A2, … , An не есть видом A (не входит как часть в целое А); неполное деление, в то время, когда не все виды (части) делимого рода (целого) названы, и сумма количеств участников деления меньше количества делимого имени.
2. Правило разграниченности. Члены деления (расчленения) должны исключать друг друга, т.е. их количества не должны иметь неспециализированных элементов при хорошего деления, и части не должны перекрывать друг друга при расчленения.
3. Правило единственности основания. Деление должно производиться по одному основанию. При исполнении этого правила предметы, входящие в количество делимого имени, наделяются одним единственным показателем – тем, что выступает в качестве основания деления. Отступление от этого правила ведет к погрешности, которая именуется смешением оснований.
Вместо термина деление время от времени в качестве синонима употребляется термин классификация. Классификация в узком смысле(конкретно в этом смысле мы будем применять этот термин в будущем) — это многоступенчатое, разветвленное деление, такое, что любой из участников, полученный в ходе данной операции, делается предметом предстоящего деления.
Соответственно хорошему и неклассическому делению направляться различать хорошую и неклассическую классификацию. Последняя именуется типологией.
За многоступенчатым и разветвленным расчленением до тех пор пока что несложного и однозначного термина не закрепилось. Эту операцию возможно назвать иерархизацией.
Классификация и иерархизация подчиняются всем правилам деления. Помимо этого, они имеют собственные особенные правила.
1. Правило последовательности. При классификации направляться от рода переходить к ближайшим видам, а при иерархизации – от целого к его частям одного и того же уровня, не пропуская их. При нарушении этого правила допускаемая погрешность – «скачком в классификации (иерархизации)».
2. Правило существенности основания. Классификация (иерархизация) обязана производиться по значительным показателям. Критерием существенности того либо иного показателя есть свойство владеющего им предмета являться средством ответа поставленной задачи.
Частным случаем расчленения есть периодизация.Её изюминкой есть, во-первых, указание на развитие отображаемого предмета во времени. Во-вторых, члены расчленения (периоды) отличаются собственной мерой как единством качественных и количественных черт предмета.
ОПРЕДЕЛЕНИЕ, Либо ДЕФИНИЦИЯ (Неспециализированная Черта)
В логике различают в первую очередь два различных смысла термина определение. Во-первых, под определением понимается операция, разрешающая выделить некий предмет среди вторых предметов, конкретно отличить его от них. Это достигается методом указания на показатель, свойственный этому, и лишь этому, предмету. Таковой показатель именуется отличительным (своеобразным). Как мы поступаем, к примеру, в случае, если требуется выделить квадраты из класса прямоугольников? Мы говорим о признаке, свойственный квадратам и не свойственный вторым прямоугольникам, –на равенство их сторон.
Во-вторых, определением именуют логическую операцию, дающую возможность раскрыть, уточнить либо организовать суть одних языковых выражений посредством вторых языковых выражений. Так, в случае, если человек не знает, что свидетельствует слово вершок, ему разъясняют, что вершок –это старая мера длины, равная 4,4 см. Потому, что человеку заблаговременно как мы знаем, что такое старая мера длины, равная 4,4 см, постольку для него делается ясным и понятным суть слова вершок.
Определение, дающеё отличительную чёрта некоего предмета, именуется настоящим. Определение, раскрывающеё, уточняющеё либо формирующеё суть одних языковых выражений посредством вторых, именуется номинальным.
Прием установления значения языкового выражения методом его яркого соотнесения с обозначаемым предметом либо его образом именуется остенсивным определением.
В структуре определения выделяется три части:
1) определяемое имя либо выражение, его содержащеё (обозначается знаком Dfd –сокращением от лат. definiendum);
2) выражение, раскрывающеё, уточняющеё либо формирующеё значение определяемого имени (обозначается знаком Dfn — сокращением лат. definiens);
3) дефинитивная связка, соотносящая Dfd и Dfn по их значению (обозначается знаком º).
Формально структура определения представляется выражением: Dfd º Dfn.
ПРАВИЛА ОПРЕДЕЛЕНИЯ
1. Правило соразмерности. Dfd и Dfn должны быть равнообъёмны.
Отклонение от правила соразмерности ведет к неточностям:
1) «через чур широкое определение» — количество Dfn больше количества Dfd;
2) «через чур узкое определение» — количество Dfn меньше количества Dfd;
3) «в один момент через чур широкое и через чур узкое определение» — количества Dfd и Dfn находятся в отношении пересечения.
4) определение через безлюдное имя — Dfd и Dfn выясняются несовместимыми.
2. Правило запрета порочного круга. Запрещается Dfd определять через Dfn, что, со своей стороны, выяснен через Dfd. Допускаемое наряду с этим нарушение именуется порочный круг в определении. Частным случаем порочного круга есть тавтология –повторение Dfd и Dfn (хотя бы и в другой словесной форме) без установления значения Dfd.
3. Правило однозначности. Каждому Dfn в точности обязан соответствовать один единственный Dfd, и напротив. Это правило ликвидирует омонимии и явления синонимии, запрещает применение метафор, художественных образов.
4. Правило простоты. Dfn обязан выражаться описательным именем, характеризующим определяемые предметы только собственными главными показателями. В другом случае определение будет избыточным. В хороших определениях это правило выполняется при условии, в случае, если: а) входящий в Dfn род есть ближайшим по отношению к Dfd, т.е. таким, что никакое второе имя, подчиненное роду и подчиняющеё Dfd, ранее не выяснено; б) в Dfn отсутствуют выражения, находящиеся в отношении следования (подчинения).
5. Правило компетентности. В Dfn смогут входить только выражения, значения которых уже приняты либо ранее выяснены. Отклонение от этого правила именуется определением малоизвестного через малоизвестное.
СОКРАЩЕННЫЕ СИЛЛОГИЗМЫ
Для интеллектуально-речевой деятельности употребляются выражения с пропущенными, но подразумеваемыми частями. К таким выражениям относятся энтимемы (от греч. en time – в уме), – сокращенные силлогизмы, в которых опускается одна из посылок либо заключение.
оценки энтимемы и Методика восстановления на её состоятельность складывается из следующих шагов:
1.Энтимема записывается в стандартном виде: имеющиеся посылки помещаются над чертой, заключение – под ней.
2.В соответствии с принятой классификацией устанавливается разновидность данного вывода (это возможно окончательный силлогизм, условный силлогизм и пр.).
3.В соответствии с определениями заключения и посылок устанавливается, какая из частей вывода есть подразумеваемой.
4.С применением правил и определений, характерных для данного класса выводов, восстанавливается недостающая часть вывода.
5.Производится анализ связей между заключением и посылками на соответствие логическим правилам. Нарушение хотя бы одного из правил говорит о наличии формальной неточности в энтимеме.
6.Производится анализ восстановленной посылки на соответствие настоящему положению дел. Её ложность свидетельствует наличие содержательной неточности в энтимеме.
РАЗДЕЛ 4. АРГУМЕНТАЦИЯ
Похожая на правду АРГУМЕНТАЦИЯ
Наиболее значимое свойство ДЕДУКТИВНОЙ АРГУМЕНТАЦИИ (верных выводов) – наличие отношения следования между заключениями и посылками, благодаря чего истинность посылок гарантирует истинность заключений. Для правдоподобной аргументации (правдоподобных выводов) характерно отсутствие этого отношения, и истинность посылок не гарантирует, но и не исключает истинности заключений, делает ее вероятной, правдоподобной. Наиболее значимыми разновидностями правдоподобной аргументации являются аналогия, абдукция и индукция
АНАЛОГИЯ
Аналогия – это вид аргументации, характеризующийся переносом показателя, свойственного одному предмету, на другой, подобный первому, предмет.
Аналогия строится по следующей схеме:
S1 имеется P1, P2, P3, … , Pn-1, Pn.
S2 имеется P1, P2, P3, … , Pn-1
S 2 имеется Pn
Тут S1 и S2 – имена сопоставляемых предметов, P1, P2, P3, … , Pn-1 – имена показателей, неспециализированных для предметов S1 и S2, Pn – имя показателя, принадлежащего предмету S1 и переносимого на предмет S2. Разрывная черта говорит о правдоподобности вывода[3].
Предмет, показатель которого переносится на другой предмет, именуется моделью; предмет, на что переносится показатель другого предмета, именуется прототипом. Наровне с термином «прототип» употребляются кроме этого термины «оригинал», «пример» и др.
Хрестоматийным примером вывода по аналогии есть рассуждение о возможности судьбы на Марсе. Приверженцы данной догадки обращают внимание на то, что между Почвой (S1) и Марсом (S2) довольно много неспециализированного: это две расположенные рядом планеты Нашей системы (P1), тут и в том месте имеется вода (P2), воздух (P3), на поверхностях этих планет примерно однообразная температура (P4) и т.д. Но на Земле имеется жизнь (Pn). Исходя из этого в полной мере правдоподобно, что и на Марсе имеется жизнь (Pn).
Аргументация по аналогии находят широкое использование в самых разнообразных сферах людской деятельности – в науке, мастерстве, повседневной жизни. В частности, мыслительные схемы, выработанные в ходе многовековой практики человечества, мы переносим на рассуждения с самым разнообразным содержанием. Ответ любой задачи связано с тем, что употребляются средства и методы, оправдавшие себя при ответе вторых задач. Происхождение многих таинственных явлений природы находит собственный объяснение по аналогии с теми предметами, сущность которых уже известна. Басни, сказки, притчи, пословицы, поговорки имеют прототипы в повседневной судьбе. Благодаря аналогии раскрывается простор для творческой фантазии, осуществляется выход людской мысли в такие сферы, где связи с настоящим миром смогут оборваться. Во многих случаях аналогия лежит в базе интуитивных познавательных процессов.
ИНДУКЦИЯ
Особенного рассмотрения заслуживает разновидность аргументации — индукция. В истории методологии и логики науки она в большинстве случаев противопоставлялась дедукции и наровне с ней, в отличие от вторых логических форм аргументации, стала широко известна.
Индукция(от лат. inductio – наведение) – форма обоснования, при которой заключение (тезис) получается методом обобщения сведений, содержащихся в посылках (доводах).
В несложном случае, то есть, в то время, когда заключение и посылка являются атрибутивными высказываниями, схема индуктивного вывода принимает следующий вид:
S1 имеется P
S2 имеется P
.
.
.
Sn имеется P
S1, S2,…… Snсуть S
Все S сущность P
Пример:
Медь – хороший проводник электричества.
Алюминий – хороший проводник электричества.
Железо – хороший проводник электричества.
Свинец – хороший проводник электричества.
Золото – хороший проводник электричества.
Медь, алюминий, железо, свинец, золото – металлы
Все металлы – хорошие проводники электричества
На похожий на правду темперамент данной аргументации показывает тот факт, что из заключения, имеющего форму «Все S сущность P», и посылки формы «S1, S2, …, Sn сущность P» вытекает любая из остальных посылок: «S1 имеется P», «S2 имеется P» и т.д. Но это редукция особенного рода: тут заключение обобщает единичные факты, находящиеся в собствености к одному и тому же классу предметов.
Бывают случаи, в то время, когда обобщающее заключение (тезис) принимается на базе высказываний, охватывающих все единичные случаи принадлежности показателя предметам некоего класса. Такая индукция именуется полной. В то время, когда, к примеру, преподаватель, сделав перекличку собственных учеников и убедившись, что любой из них присутствует на уроке, с удовлетворением подмечает, что все его ученики явились на урок, то он рассуждает в соответствии с принципом полной индукции. В других случаях индукция именуется неполной.
При полной индукции заключение (тезис) с необходимостью вытекает из посылок. Исходя из этого ее правомерно вычислять дедуктивным выводом. (Не просто так полную индукцию время от времени именуют индуктивным силлогизмом.)
Неполная индукция подразделяется на несложную и научную. Для несложной индукции характерен чисто формальный подход, в то время, когда обобщение делается на базе первых попавшихся, а следовательно, случайных фактов. Исходя из этого существует настоящая опасность фальшивого заключения. Так, созерцая животный мир, возможно найти следующие сходные факты:
У человека нижняя челюсть есть подвижной.
У лошади – то же самое.
У гуся – то же самое.
У щуки – то же самое.
У змеи – то же самое.
Эти факты, на основании знания о том, что человек, лошадь, гусь, щука, змея – позвоночные животные, «наводят» на заключение:
Все позвоночные животные имеют подвижную нижнюю челюсть.
Но возможность истинности этого заключения выясняется равной нулю, потому что имеется факты, противоречащие ему. К примеру, у крокодила подвижной есть не нижняя, а верхняя челюсть.
Научная индукция опирается в собственных посылках не на всякие, а на значительные показатели разглядываемого класса предметов. Обнаружение таких показателей требует целенаправленного отбора посылок в соответствии с выработанными в науке критериями и методами. Зайдя в церковь и заметив громадную массу молящихся людей, легко поддаться внушению и сделать вывод о целой религиозности населения данной местности. Но для того чтобы рода обобщения по первому впечатлению противоречат научному подходу. Дабы изучить степень религиозности населения в некоей местности, ученый-социолог совершит громадную подготовительную работу: выделит разные группы людей, распределив их по роду занятий, образованию, возрасту, месту проживания и т.д., установит количественные отношения между ними, шепетильно сформулирует и отберет анкетные вопросы, подвергнет статистической обработке полученные ответы и т.д. Так, посылки научной индукции – это не просто какие-то случайные сведения, а эти опыта с дополнительными показателями, разрешающими вскрыть значительное в изучаемом предмете – некую закономерную сообщение. Ясно, что при научной индукции степень возможности заключения существенно выше, чем при несложной индукции.
АБДУКЦИЯ