1. Матрица. Виды матриц (матрица-строчок, матрица-столбец, нулевая, диагональная, квадратная, единичная матрицы). Действия над матрицами (сложение, умножение на число, произведение, транспонирование матриц).
2. Определители 1-го, 2-го и 3-го порядков. Способ треугольников для вычисления определителя 3-го порядка. алгебраическое дополнение и Минор. Разложение определителя по элементам строчка (столбца).
3. Невырожденная матрица. Обратная матрица. Способ нахождения обратной матрицы.
4. Ответ совокупностей линейных уравнений (способ Крамера, способ обратной матрицы, способ Жордана-Гаусса).
5. Ранг матрицы.
6. Векторы. Модуль вектора. Коллинеарные и компланарные векторы. Сложение векторов, умножение вектора на число.
7. линейная зависимость и Линейная комбинация векторов. Свойства линейно зависимой совокупности векторов.
8. Размерность пространства, базис пространства. Координаты вектора в данном базисе. Ортонормированный базис. Направляющие косинусы вектора.
9. Ориентация троек векторов. Скалярное, векторное и смешанное их свойства и произведения векторов.
10. Линейные операторы. Матрица линейного оператора. собственные векторы и Собственные числа матрицы линейного оператора
Аналитическая геометрия.
11. Прямая на плоскости. Виды уравнений прямых. Угол между прямыми. Условие параллельности, перпендикулярности двух прямых. Расстояние от точки до прямой.
12. Плоскость. Виды уравнений плоскостей. Угол между плоскостями. Условие параллельности, перпендикулярности двух плоскостей. Расстояние от точки до плоскости.
13. Прямая в пространстве. Виды уравнений прямых. Угол между прямыми. Угол между плоскостью и прямой. Условие параллельности, перпендикулярности, компланарности двух прямых.
14. Кривые второго порядка (эллипс, окружность, преувеличение, парабола). Определение, канонические уравнения, характеристики.
Введение в анализ.
15. Функция. область значений и Область определения функции. Сложная, обратная, параметрически заданная функции.
16. Предел функции. Единственность предела функции в точке. Бесконечно малые (б.м.)и вечно громадные(б.б.) функции. Свойства б.м. и б.б. функций.
17. Главные теоремы о пределах.
18. Превосходные пределы. Эквивалентные функции.
19. Односторонние пределы.
20. Непрерывность функции. Точки разрыва и их классификация.
Дифференциальное и счисление функции одной переменной.
21. Производная функции в точке. Дифференцируемость функции в точке и на промежутке. Геометрический и физический суть производной. нормали и Уравнение касательной к кривой.
22. Главные правила дифференцирования. Производная сложной, обратной и параметрически заданной функции.
23. Дифференциал функции.
24. Правило Лопиталя.
25. убывание и Возрастание функции. убывания функции и Достаточное условие возрастания.
26. минимума и Точки максимума. Теорема Ферма (Нужное условие существования точек экстремума). Достаточное условие существования точек экстремума.
27. Выпуклость, вогнутость графика функции. Точки перегиба. Достаточное условие выпуклости, вогнутости графика функции. Нужное и достаточное условия существования точки перегиба.
28. Асимптоты графика функции. Способы нахождения вертикальных, наклонных и горизонтальных асимптот.
29. Громаднейшее и мельчайшее значения функции на отрезке. Теорема Вейерштрасса.
Функция нескольких переменных.
30. Определение функции двух переменных. непрерывность и Предел функции двух переменных в точке.
31. Частные производные функции двух переменных и их геометрический суть. Касательная нормаль и плоскость к поверхности, заданной графиком функции z=f(x,y) в точке.
32. Частные производные высших порядков. Теорема о равенстве смешанных частных производных.
33. Полный дифференциал функции. Формула для приближенного вычисления значения функции посредством полного дифференциала.
34. Производная по направлению, градиент функции.
35. Экстремум функции двух переменных, громаднейшее и мельчайшее значения функции в замкнутой ограниченной области.
Приложения
| ВЕКТОРЫ | |||||||||||||
| Координаты точки М имеется координаты радиус-вектора | ; | ||||||||||||
| Вектор ; где , | |||||||||||||
| Вектор | |||||||||||||
| Протяженность вектора | 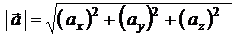
|
||||||||||||
| Орт : ( ) | 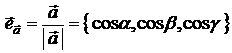
|
||||||||||||
| Направляющие косинусы : | 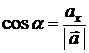 , , 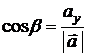 , , 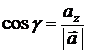 ; ;
|
||||||||||||
| Проекция вектора на вектор | , где – угол между и . | ||||||||||||
| Равенство векторов | 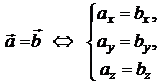
|
||||||||||||
| Коллинеарность векторов | 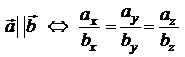 (координаты пропорциональны) |
||||||||||||
| Линейные операции над векторами | |||||||||||||
| Сумма (разность) векторов | . | ||||||||||||
| Умножение вектора на число | |||||||||||||
| Определение, формулы | Свойства, приложения | ||||||||||||
| Скалярное произведение двух векторов | |||||||||||||
| , где – угол между . | 1. ; 2. ; 3. 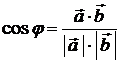 ; 4. ; 4. 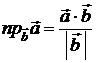 ; 5. ; 6. , в частности: . ; 5. ; 6. , в частности: . |
||||||||||||
| Векторное произведение двух векторов | |||||||||||||
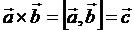 , удовлетворяет условиям: 1. ; 2. ; 3. образуют правую тройку. , удовлетворяет условиям: 1. ; 2. ; 3. образуют правую тройку. 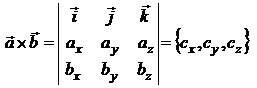
|
1. ; 2. ; 3. ; 4. ; 5. ; 6. 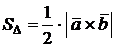 ; ; 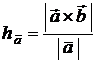 . . |
||||||||||||
| Смешанное произведение трех векторов | |||||||||||||
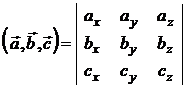
|
1. не изменяется при циклической перестановке; 2. меняет символ при перемене мест любых двух векторов; 3. 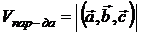 ; ; 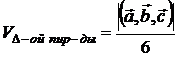 3. 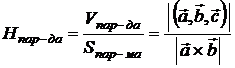 ; 4. –компланарны . ; 4. –компланарны . |
||||||||||||
| ПРЯМАЯ НА ПЛОСКОСТИ | |||||||||||||
| Уравнение с угловым коэффициентом | 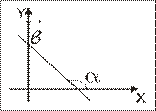
|
– угловой коэффициент прямой; –отрезок,отсекаемый прямой на оси . | |||||||||||
| Неспециализированное уравнение | 
|
нормаль . | |||||||||||
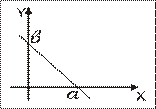
Уравнение в отрезках 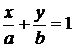
|
|
– отрезки, каковые отсекает прямая на осях координат соответственно. | |||||||||||
Каноническое уравнение 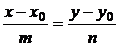
|

|
точка , направляющий вектор . | |||||||||||
Параметрические уравнения 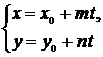
|
|||||||||||||
| Обычное уравнение | 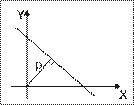
|
– орт ; – расстояние от до прямой . | |||||||||||
| Уравнение прямой, проходящей через | две точки , | 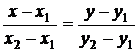
|
|||||||||||
| угловой коэффициент и точку | |||||||||||||
| нормаль и точку | |||||||||||||
| точку и направляющий вектор | 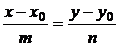
|
||||||||||||
| КРИВЫЕ ВТОРОГО ПОРЯДКА НА ПЛОСКОСТИ | |||||||||||||
| Кривая II порядка, центр в точке | График кривой, где | Характеристики кривой | |||||||||||
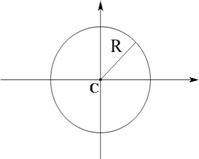
| Окружность , |
|
радиус окружности R. | |||||||||||
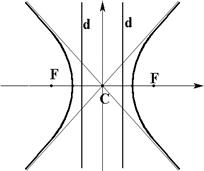
Эллипс 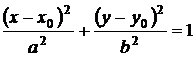
|
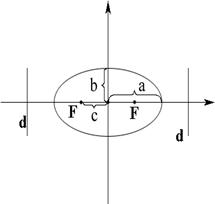
|
; фокусы лежат на большей оси, равной ; эксцентриситет ; директрисы перпендикулярны большей оси. |
|||||||||||
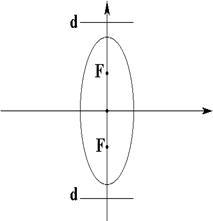
|
; фокусы лежат на большей оси, равной ; эксцентриситет ; директрисы перпендикулярны большей оси. |
||||||||||||
Преувеличение 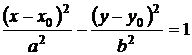
|
 ; асимптоты: 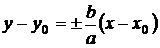 . . 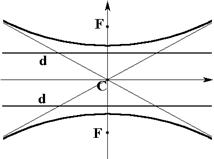
|
вершины фокусы лежат на настоящей оси ; эксцентриситет ; директрисы перпендикулярны настоящей оси. | |||||||||||
Преувеличение 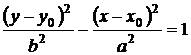
|
вершины фокусы лежат на настоящей оси ; эксцентриситет ; директрисы перпендикулярны настоящей оси. |
||||||||||||
| Парабола |
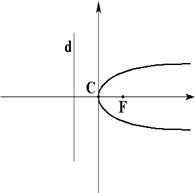
|
фокус лежит в параболы на оси симметрии эксцентриситет ; директриса ; , то ветви вправо; , то ветви влево. |
|||||||||||
| Парабола |
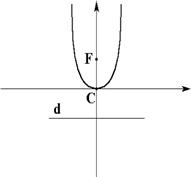
|
фокус лежит в параболы на оси симметрии эксцентриситет ; директриса ; , то ветви вверх; , то ветви вниз. |
|||||||||||
| Прямая и ПЛОСКОСТЬ В ПРОСТРАНСТВЕ | |||||||||||||
| Плоскость в пространстве | |||||||||||||
| Неспециализированное уравнение | нормаль | ||||||||||||
Уравнение в отрезках 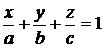
|
– отрезки, каковые отсекает плоскость на осях координат | ||||||||||||
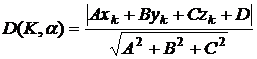
|
расстояние от точки до плоскости : |
||||||||||||
| Уравнение плоскости, проходящей через | точку и нормаль |
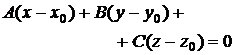
|
|||||||||||
| три точки , и | 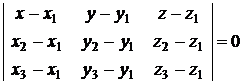
|
||||||||||||
| Прямая в пространстве | |||||||||||||
Каноническое уравнение 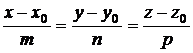
|
точка , направляющий вектор . | ||||||||||||
Параметрическое уравнение 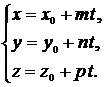
|
|||||||||||||
Пересечение двух плоскостей 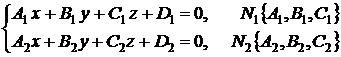
|
находим из СЛУ 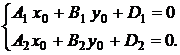
|
||||||||||||
| Уравнение прямой, проходящей через | точку и | 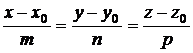
|
|||||||||||
| две точки и |
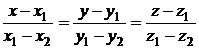
|
||||||||||||
| ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА – это геометрическое место точек пространства, координаты которых в декартовой совокупности координат являются уравнениями второго порядка. | |||||||||||||
| сфера | 
|
||||||||||||
трехосный эллипсоид 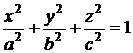
|
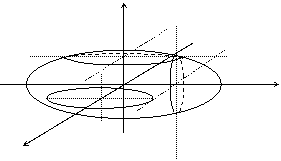
|
||||||||||||
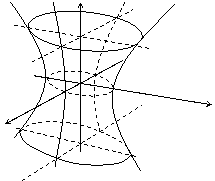
однополостный гиперболоид 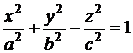
|
|
||||||||||||
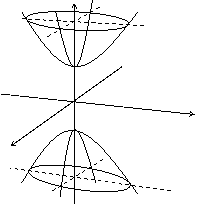
двуполостный гиперболоид 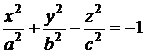
|
|
||||||||||||
эллиптический параболоид 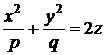 , ,
|

|
||||||||||||
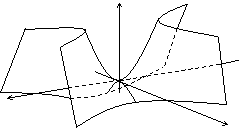
гиперболический параболоид 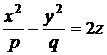
|
|
||||||||||||
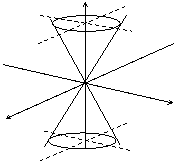
конус второго порядка 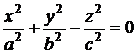
|
|||||||||||||
| ЦИЛИНДРИЧЕСКИЕ ПОВЕРХНОСТИ | |||||||||||||
эллиптический цилиндр 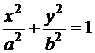
|

|
||||||||||||
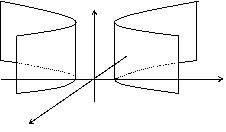
гиперболический цилиндр 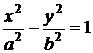
|
|
||||||||||||
| параболический цилиндр | 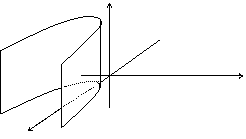
|
||||||||||||
| ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ | ||
| Правила нахождения производных | ||
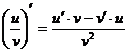
|
||
| Формула логарифмического дифференцирования | Производная обратной функции 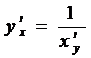
|
Производная функции, заданной параметрически 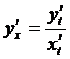
|
| Таблица производных | ||
| 1. | 2. | |
| 3. | 4. 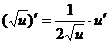
|
|
| 5. | 6. | |
7. 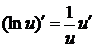 дтн дтн |
8. 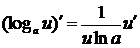
|
|
| 9. | 10. | |
11. 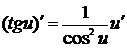
|
12. 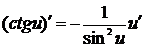
|
|
13. 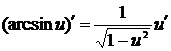
|
14. 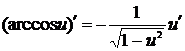
|
|
15. 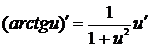
|
16. 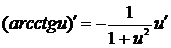
|
|
| 17. | 18. | |
 нормаль и Касательная к графику функции в точке нормаль и Касательная к графику функции в точке-уравнение касательной |
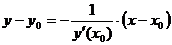 -уравнение нормали
-уравнение нормали
где
Светлана Геннадьевна Антипина
Методические указания, контрольные работы
по дисциплине «Математика»
для студентов профессии 190601.65 (150200)
«автомобильное хозяйство и Автомобили»
В авторской редакции
Темплан 2009, поз.№ 24 В (З)
Лицезия ИД № 04790 от 25.10.2009
Подписано на «Выпуск в свет»- 25.10.09.
Уч.-изд.л. 2,44.
На электронном носителе
Волгоградский национальный технический университет.
400131 Сталинград, пр. Ленина, 28.