Замысел:
1. Задача расширения понятия числа. Краткие исторические сведения о происхождении отрицательного числа и понятия дроби. Целые числа. Отрицательные целые числа. Целое отрицательное число. Противоположное число. Модуль числа. Сумма, произведение, разность двух целых чисел. Свойства множества целых чисел и их геометрическая интерпретация.* (вводится позднее)
СВОЙСТВА МНОЖЕСТВА ЦЕЛЫХ ЧИСЕЛ.
Теорема 8.22. (Теорема Архимеда). Для любых целых чисел а и в существует натуральное число п, что пв а.
Подтверждение. Разглядим число п = а’, т.е. п = а + 1. В силу теоремы 8.9 и следствия 2 имеем неравенства в 1 и п а. Почленно перемножая эти неравенства, возьмём пв а. Теорема доказана.
Теорема 8.23. (Принцип мельчайшего числа). Любое непустое подмножество множества целых чисел содержит мельчайшее число.
Подтверждение. Пускай множество М таково, что М I Z и
М ¹ ?. Разглядим два случая.
I. Множество М складывается из конечного числа элементов. В этом случае доказательно теоремы проводим способом математической индукции по числу элементов. В случае, если М складывается из одного элемента (М = {а}), то данный элемент и будет мельчайшим из чисел, входящих в М. Предположим, что теорема честна для множества М, содержащего некое конечное число элементов п. Иначе говоря думаем, что всякое множество М I Z, складывающееся из п элементов, содержит мельчайшее число. Пользуясь предположением, докажем, что множество М I Z, складывающееся из
п + 1 элементов, кроме этого содержит мельчайшее число. Выберем произвольный I элемент аIМ и разглядим множество М? = М\{а}. Множество М? складывается из п элементов, соответственно по предположению в нем найдется мельчайшее число, которое обозначим через в. Так как аI М?, а вI М?, то а ¹ в, но тогда по теореме 8.10 из двух чисел а и в одно меньше другого. Мельчайшее из двух чисел а и возначим через с. Разумеется, что с есть мельчайшим числом в множестве М.
Итак, все условия способа математической индукции выполнены и справедливость теоремы для любого конечного подмножества доказана.
II. Пускай сейчас множество М складывается из нескончаемого числа элементов. Выберем любой элемент n из множества М. Число n разбивает множество М на два подмножества:
М? = {х/хIМ , х ? п}и М? = {х| хIМ х п }. Множество М? складывается из конечного числа элементов (их не более чем п + 1), соответственно по первой части теоремы, в нем содержится мельчайшее число, которое обозначим через т. Итак, для любого хIМ? , имеем т ? х. В частности, т ? п. Но тогда, учитывая определение множества М?, приходим к выводу, что мельчайшее число во всем множестве т . Теорема доказана.
Теорема 8.24. {Принцип наибольшего числа). В случае, если М — непустое подмножество множества целых чисел и существует такое число в, что для любого числа хI М выполняется неравенство х
Подтверждение теоремы подобно доказательству теоремы 8.23.
Теорема 8.25. {Свойство дискретности множества Z). Для любого
аI Z не существует целого числа п для того чтобы, что а п а’.
Подтверждение совершим способом от противного. Пускай существует такое п, что выполняются оба неравенства: а п и п а’. По определению отношения меньше существуют такие целые числа с? и с?, такие, что а + с? = п и п + с?= а’. Тогда а + (с? + с?) = а ‘ т.е. с? + с? = 1. Иначе,
с? ?1 и с? ? 1, исходя из этого с? + с? ? 2. Пришли к несоответствию с допущением, значит, оно неверное. Теорема доказана.
Теорема 8.26. Множество целых чисел Z: а) нескончаемое; б) дискретное; в) линейно упорядоченное; г) счетное, д) в нем имеется мельчайшее число и нет наибольшего числа; е) в нем выполняются правила мельчайшего и наибольшего числа и свойство Архимеда.
Подтверждение, а) В множестве Zесть личные подмножества, каковые ему эквиваленты. К примеру, множество четных целых чисел есть подмножеством Zи ему эквивалентно, исходя из этого множество Zбесконечное; б) Свойство доказано в теореме 8.25; в) Свойство доказано в теореме 8.10; г) Свойство направляться из определения счетного множества: д) Свойство доказано в теореме 8.9 и следствиях нему; е) Свойство доказано в теоремах 8.23 и 8.24.
АКСИОМАТИЧЕСКОЕ ПОСТРОЕНИЕ МНОЖЕСТВА ЦЕЛЫХ НЕОТРИЦАТЕЛЬНЫХ ЧИСЕЛ Z?. Множество Z? = NE{0}. Нуль возможно ввести, поменяв I и IV теоремы Пеано следующим образом:
I. В множестве Z? существует элемент, конкретно не следующий ни за каким элементом этого множества. Именуют его нулем и обозначают знаком 0.
IV. Пускай множество М имеется подмножество множества Z? и как мы знаем, что:
а) 0IМ; б) из того, что аIМ , направляться, что и а’IМ. Тогда множество М сходится с множеством Z?.
Теоремы II и III остаются без трансформации.
умножения целых и Свойства сложения неотрицательных чисел принимают вид: $
Для сложения: 1) (а IZ?)[а + 0 = а]; 2) (а,в IZ?)[а + в’ = (а + в)’}.
Для умножения: 1) (а IZ?)[а·0 = 0]; 2) (а,в IZ?)[а·в’ = а·в + а]. деления операций целых и Определения вычитания неотрицательных чисел подобны соответствующим определениям операций для натуральных чисел. Наряду с этим уверены в том, что деление на нуль нереально: значение 0:0 не выяснено, в частности а:0 при а ¹ 0 не существует.
Отношение меньше (больше) на множестве Z?, определяется равно как и на множестве N. Причем, числом, которое меньше любого другого числа, есть число нуль и оно в числовом последовательности стоит на первом месте: 0, 1,2,3,….
Все теоремы, доказанные для натуральных чисел, остаются в силе для целых неотрицательных чисел.
ТЕОРЕТИКО-МНОЖЕСТВЕННОЕ ПОСТРОЕНИЕ МНОЖЕСТВА ЦЕЛЫХ НЕОТРИЦАТЕЛЬНЫХ ЧИСЕЛ. Число — одно из главных понятий математики, появившееся в первый раз в связи с потребностями счета предметов. Построение совокупности целых неотрицательных чисел на базе теории множеств связано с именем Г. Кантора. В данной теории, которую именуют количественной теорией, основополагающими являются понятия конечного множества и взаимно однозначного соответствия.
С теоретико-множественных позиций натуральное число рассматривается как число элементов конечного множества. Число 0 также имеет теоретико-множественное истолкование: оно соответствует безлюдному множеству (0 = п(0)). Так как одному и тому же множеству соответствует лишь одно число, то вся совокупность конечных множеств распадается на классы равночисленных (эквивалентных) множеств. Исходя из этого натуральным числом именуют неспециализированное свойство (инвариант) класса непустых эквивалентных множеств. Так, число 5 — то неспециализированное свойство, которым владеют множества, содержащее пять пальцев, пять вершин пятиконечной звезды, пять сторон пятиугольника и т.п. Любой класс определяется любым своим представителем, к примеру, отрезком натурального последовательности.
Два натуральных числа именуются равными, в случае, если соответствующие им множества эквивалентны, в другом случае — числа именуются неравными, т.е. в случае, если а = п(А), в = п(В), то а=в U А~В и а¹в U А~В.
Теорема 8.27. Отношение равенства целых неотрицательных чисел владеет следующими особенностями:
1. Рефлексивность. Любое целое неотрицательное число равняется самому себе, т.е. а = а.
2. Симметричность. В случае, если число а равно в, то и число в равно а, т.е. в случае, если а = в, то в = а.
3. Транзитивность. Два числа, равные третьему, равны между собой, т.е. в случае, если а = в и в = с, то а = с.
Подтверждение. Каждое из этих особенностей вытекает из одноименного свойства отношения равномощности определения и множеств равенства натуральных чисел.
Следствие. Отношение равенства целых неотрицательных чисел есть отношением эквивалентности.
Отношение меньше также имеет теоретико-множественное истолкование. В случае, если множество А равномощно собственному подмножеству множества В и п{А} = а, п(В) = в, говорят, что число а меньше числа в, и пишут а в. В данной же ситуации говорят, что в больше а, и пишут в а.
Теорема 8.28. Отношение меньше на множестве Z? владеет следующими особенностями:
1. Для любого хорошего от нуля числа а справедливо неравенство 0 а.
2. Антирефлексивность. Любое целое неотрицательное число не вступает в отношение меньше с самим собой, т.е. неверно, что а а) ].
3. Асимметричность. В случае, если а в, то неверно, что в а.
4. Транзитивность. В случае, если а в, в с, то а с.
Подтверждение. 1. Свойство вытекает из того, что безлюдное подмножество есть подмножеством любого множества А, для которого а = п(А), и теоретико-множественного определения отношения меньше и того факта, что 0 = п(0)).
2. Справедливость свойства вытекает из того, что конечное множество не может быть равномощно собственному подмножеству.
3. Справедливость свойства вытекает из следующих рассуждений: в случае, если конечное множество А равномощно собственному подмножеству множества в, то множество в не может быть равномощно никакому собственному подмножеству множества А, т.к. в другом случае мы взяли бы, что А равномощно некоей собственной части, что противоречит конечности множества А.
4. Свойство вытекает из транзитивности отношения строгого включения для множеств (АIВUВIС = АIС). Теорема доказана.
Следствие. Отношение меньше определяет на множестве целых неотрицательных чисел строгий порядок, что есть линейным в силу свойства связности: в случае, если а ¹ в, то или а в, или в а.
ПОРЯДКОВЫЕ И КОЛИЧЕСТВЕННЫЕ ЧИСЛА. В аксиоматической теории натуральное число рассматривается как элемент особого множества, представляющего собой нескончаемый упорядоченный последовательность, в котором непременно существует первое число (первый элемент) и следующие за ним числа находятся в определенном порядке. Иначе говоря аксиоматическая теория разглядывает натуральное число, как число порядковое.
В теоретико-множественной трактовке натуральное число понимается как, количественная черта конечного множества, т.е. как число количественное.
Эти два разные смысла натурального числа связаны между собой в ходе счета предметов, т.к. при пересчете элементов некоего множества не| лишь находят, сколько в нем элементов (пять, двадцать один и т.п.), но и расставляют эти элементы в определенном порядке (упорядочивают их: пери второй, третий и т.д.). Так, к примеру, упорядочиваются в театрах кресла и ряды, на вешалках — крючки для одежды, на улицах — дома, в каждом доме — этажи квартиры и т. п. Исходя из этого натуральные числа помогают не только для ответа вопрос какое количество?, но и для ответа какой по счету?, т.е. они являются не только количественными, но и порядковыми числами.
При счете элементов некоего конечного множества А принципиально важно выполнять следующие требования: 1) затевать счет возможно с любого элемента множества; 2) ни один элемент множества А не должен быть пропущен; 3) ни один элемент множества не должен быть сосчитан два раза; 4) первым при счете именуется слово «один»; 5) числа, применяемые при счете, следуют одно за вторым без пропусков.
АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ НА МНОЖЕСТВЕ Z? (ТЕОРЕТИКО-МНОЖЕСТВЕННЫЙ ПОДХОД). Сложение целых неотрицательных чисел связано с операцией объединения непересекающихся конечных множеств.
Сумма целых неотрицательных чисел а и в — число элементов в объединении непересекающихся множеств А и В таких, что п(А) = а, п(В) = в, т.е. а + в = п(АEВ). где а = п(А), в = п(В), АCВ=0.
Теорема 8.30. Для любых целых неотрицательных чисел а и в постоянно существует единственное целое неотрицательное число с, являющееся их суммой, т.е. сумма любых двух целых неотрицательных чисел существует и единственна.
Подтверждение. Пускай а и в — два целых неотрицательных числа. Из элементов любой природы выстроим конечные множества А и В такие, что п(А) = а, п(В) = в и АCВ=0.
Докажем существование. Из теории множеств как мы знаем, что объединение конечного числа конечных множеств имеется множество конечное. Исходя из этого объединение АEВ есть конечным множеством. Последнее свидетельствует, что существует целое неотрицательное число с = пАEВ). Но по определению суммы целых неотрицательных чисел число с и имеется сумма чисел а и в. Тем самым существование суммы доказано.
Докажем единственность. Продемонстрируем, что сумма а + в единственна и не зависит от выбора представителей в классах. Заберём из классов эквивалентности, определяющих числа а и в, вместо множеств А и В соответственно, множества А? и В?. Пускай с? — целое неотрицательное число такое, что п(А?E В?) = с?. Продемонстрируем, что с? = с. В противном случае говоря, докажем, что в случае, если А?~А и В?~В, причем А? C В? = А C В = ? , то А?E В?~ АE В.
Пускай j- взаимно однозначное соответствие между множествами А и А, а y — между множествами В и В?. Любой элемент х, находящийся в собствености АE В, в собственности или А, или В, в силу того, что х не имеет возможности принадлежать А и В в один момент, т.к. их пересечение пусто.
Определим соответствие f между множествами АE Ви А?E В? следующим образом.
В случае, если хIА, то положим f(х) = j(х) = х? IА.
В случае, если хIВ, то положим f (х) = y (х) = х? IВ.
Продемонстрируем, что f взаимно однозначное соответствие. В действительности, при таком определении для каждого х существует единственный элемент , удовлетворяю условию j(х) = f (х). И напротив, каждый элемент х? соответствует совершенно верно одному элементу хеАE В. Следовательно, взаимно однозначное соответствие f между множествам АE В и А?E В? установлено. Исходя из этого АE В ~ А?E В?, соответственно с? = с. Теорема доказана.
Определение суммы двух целых неотрицательных чисел легко распространяется на любое конечное число слагаемых.
Вычитаниецелых неотрицательных чисел а и в связано с выделением из множества А (а = п(А)) подмножества В (в = п(В)).
Разность целых неотрицательных чисел а и в — число элементов в дополнении множества В до множества А при условии, что п(А) = а, п(В) = в, ВIА, т.е.
а-в=п(А\В).
Теорема 8.31. Разность целых неотрицательных чисел а и всуществует и единственна тогда и лишь тогда, в то время, когда в ? а, т.е.
(а,вIZ?)($сIZ?)[с = а — в в ? а].
I. Необходимость условия существования разности;
II. Достаточность условия существования разности;
III. Единственность разности.
В количественной теории рассматриваются разные подходы к определению произведения целых неотрицательных чисел. Так, забрав за базу понятие суммы, имеем следующее определение.
Произведением целых неотрицательных чисел а и а – целое неотрицательное число ав, которое удовлетворяет следующим условиям:
1) а*в = а+а+…+а (в раз) при в 1;
2) а*1 = а при в = 1;
3) а*0 = 0.
Данное определение имеет следующее теоретико-множественное обоснование. Пускай даны в попарно непересекающихся множеств А?, А?, …, А, каждое из которых имеет а элементов. Тогда их объединение содержит ав элементов.
единственность и Существование произведения целых неотрицательных чисел при таком подходе вытекает из единственности и существования суммы.
Но для вывода законов умножения, и законов, связывающих умножение с другими операциями над целыми неотрицательными числами, более эргономичен второй подход к определению произведения. Он связан с декартовым произведением множеств.
Произведение целых неотрицательных чисел а и в – число элементов декартова произведения множеств А и В, где п(А) = а, п(В) = в, т.е. а*в = п(АВ), где а = п(А), в = п(В).
Потом доказывается теорема о единственности и существовании произведение целых неотрицательных чисел (в данном пособии берем без доказательства).
Деление чисел связано с разбиением конечных множеств на равночисленные попарно не пересекающиеся подмножества. Наряду с этим решаются две задачи: нахождение числа элементов в каждом подмножестве (деление на части) и нахождение числа таких подмножеств (деление по содержанию).
Пускай а = п(А) и множество А разбито на попарно не пересекающиеся равномощные подмножества. Частным чисел а и в именуется:
— число подмножеств в этом разбиении, в случае, если в – число элементов каждого подмножества в разбиении множества А;
— число элементов в каждом подмножестве, в случае, если в – число подмножеств в разбиении множества А.
Частное обозначается а:в.
В случае, если даны числа а и в такие, что а = п(А), в = п(В), а в, и множество А возможно разбить на п подмножеств, равномощных множеству В, то говорят, что число а больше в в п раз, а число в меньше числа а в п раз.
Невозможность деления на нуль кроме этого имеет собственный теоретико-множественное истолкование. В случае, если а¹ в, а в= 0, то невозможность деления я на в вытекает из неосуществимости представления непустого конечного множества А (п(А) = а) в виде объединения безлюдных подмножеств.
СВОЙСТВА и ЗАКОНЫ АРИФМЕТИЧЕСКИХ ОПЕРАЦИЙ НА МНОЖЕСТВЕ Z? полностью совпадают с свойствами и аналогичными законами арифметических операций на множестве N.
Применяя теоретико-множественную трактовку gокажем фундаментальные законы, которым удовлетворяют арифметические операции на множестве целых неотрицательных чисел.
Теорема 8.33. Для любых целых неотрицательных чисел а, d и с честны следующие законы арифметических операций:
1. Коммутативности: а + d = d + а, а*в = в*а.
2. Ассоциативности: (а + в) + с = а + (в + с), (а*в)*с = а*(в*с).
3. Дистрибутивности:
левый и Правый дистрибутивные законы умножения относительно сложения: (а + в)с = ас + вс; с(а + в) = са + св;
левый и Правый дистрибутивные законы умножения относительно вычитания: (а — в)с = ас — вс; с(а — в) = са — св.
Подтверждение. 1. Докажем коммутативный закон сложения. Выстроим такие конечные множества А и В, что п(А) = а, п(В) = в и АCВ = ?. Для любых множеств честен коммутативный закон объединения АEВ = ВEА (доказано ранее). Равные конечные множества имеют равные численности, т.е. п(АEВ) = п(ВEА). По определению суммы целых неотрицательных чисел п(АEВ) = п(А) + п(В) = а + в, п(ВEА) = п(В) + п(А) = в + а. Следовательно, а + в = в + а правильно для любых целых неотрицательных чисел.
2. Подтверждение ассоциативного закона сложения опирается на ассоциативность объединения множеств А, В и С проводится подобно доказательству прошлого закона.
3. Доказательства остальных законов проводятся подобно. Теорема доказана.
Увидим, что коммутативный и ассоциативный законы сложения распространяются на любое конечное число слагаемых, а коммутативный и ассоциативный законы умножения честны для любого конечного числа множителей.
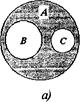
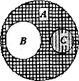
Дадим теоретико-множественное обоснование правила вычитания суммы из. С целью этого разглядим три конечных множества А, В и С таких, что п(А) = а, п(В) = в, п(С) = с, ВCС= ? и ВEСI А. Тогда а — (в + с) = п(А\( ВEС), а (а- в) — с = п((А\В)\С). На диаграммах Эйлера-Венна множество А\(ВEС) представлено заштрихованной частью на рис.а, а множество (А\В)\С — двояко заштрихованной частью на рис.б. Сравнивая указанные области, убеждаемся в том, что они однообразны. Значит, для указанных выше множеств А, В и С выполняется равенство А\(ВEС) = (А\В)\С. Следовательно, п(А\(ВEС)} = п{(А\В)\С), т.е. а — (в + с) = (а — в) — с. Подобно рассуждая, возможно дать теоретико-множественное обоснование остальным правилам.
Правила деления суммы, произведения и разности на число кроме этого имеют теоретико-множественное обоснование. Пускай а = п(А), в = п(В) и АC?В = ?. В случае, если каждое из множеств А и В возможно разбить на с подмножеств, то разумеется, что их объединение АEВ кроме этого разбивается на с подмножеств. Наряду с этим, в случае, если каждое подмножество в разбиении множества А содержит а: с элементов, каждое подмножество в разбиении В — в:с элементов, то каждое подмножество в разбиении объединения содержит а:с + в:с элементов. Это указывает, что (а + в):с = а:с + в:с. Подобно рассуждая, возможно дать теоретико-множественное обоснование остальным правилам.
МНОЖЕСТВО ЦЕЛЫХ ЧИСЕЛ Z. потребности и Практическая деятельность самой математики приводят к необходимости расширения множества неотрицательных чисел. Так, температура окружающей среды 1° не определяет нагретость воздуха без указания — 1° холода либо тепла, информация АЗС находится в 2 км от перекрестка не определяет ее местонахождения, т.к. не указано, в какую сторону от перекрестка нужно двигаться к АЗС: влево либо вправо, и т.п. В математике кроме этого имеется последовательность задач, неразрешимых во множестве целых неотрицательных чисел. К примеру, никакое целое неотрицательное число х не может быть ответом уравнения в + х = а, в случае, если а в и а, в IZ?. Неразрешимость таких задач ведет к необходимости увеличить множество Z?.
Числа вида -п, где пIZ?, именуются отрицательными целыми числами. Множество всех отрицательных целых чисел обозначают знаком Z_. Числа п и -п именуются противоположными, причем уверены в том, что -(-п) = п. Число 0 не относится ни к хорошим, ни к отрицательным числам. Противоположные числа на числовой оси изображаются точками, симметричными относительно начала координат.
Объединение множеств Z?, Z_ и {0}именуют множеством целых чисел и обозначают символомZ.
АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ НА МНОЖЕСТВЕ Z .
Модуль(полная величина) числа пIZ — само это число, если оно неотрицательно, и противоположное ему число -п, если оно отрицательно (обозначается |п|), т.е.
п, в случае, если п IZ?
IпI
-песли пI Z_.
Теорема 8.34. Для п I Z выполняются следующие равенства:
1) -пg = (-1 )-п; 5) (-п)*т = -п*т;
2) (-1)*(-1 ) = 1; 6) п — т = п + (-т) = -(т — п);
3) -(-л) = п; 7) (-п) + (-т) = — (п + т);
4) (-п)*(-т) = п*т;  -0 = 0.
-0 = 0.
Подтверждение данной теоремы опускается.
Эти свойства разрешают сформулировать умножения целых и правила сложения чисел, каковые можно считать определениями данных операций.
Правило 1. (Правило сложения). При сложении двух целых чисел с однообразными символами получается число того же символа, модуль которого равен сумме модулей слагаемых. При сложении чисел с различными символами получается число, символ которого сходится со знаком слагаемого, имеющего больший модуль, а модуль равен разности модулей слагаемых. Сумма противоположных чисел равна нулю, а сумма данного нуля и числа равна данному числу.
Правило 2. (Правило умножения). При умножении двух целых чисел получается число, модуль которого равен произведению модулей множителей, а символ хорош, в случае, если символы множителей однообразны, и отрицателен, в случае, если множители имеют различные символы. В случае, если хотя бы один из множителей равен нулю, то произведение равняется нулю.
Операция вычитания в силу свойства 6 теоремы 8.34 сводится к операции сложения.
Разность двух целых чисел п и т- целое число r, вычисляемое по правилу:
r = п + (-т), т.е. разность двух целых чисел п и m имеется сумма целого числа п и числа (-т), противоположному числу т. Разность чисел п и т записывают в виде п- т, число и именуют уменьшаемым, а число т — вычитаемым.
Множество Z замкнуто относительно операций сложения, вычитания и умножения.
Частное отделения целого числа п на целое числот— такое целое число р (если оно существует), которое удовлетворяет равенству п = т р. Частное чисел п и т записывают в виде п : т либо п/т, число п именуют делимым, а число т — делителем. В множествеZ , как и в множестве N операция деления не всегда выполнима — не для любой пары целых чисел п и т существует их частное. Исходя из этого множество Z (как и N ) не замкнуто относительно операции деления. Но между операциями деления в множестве N и в множестве Zесть одно значительное различие. В множестве N в случае, если частное двух натуральных чисел существует, то оно единственно (см. теорему 8.14). В множестве Zэто не так. В случае, если п — произвольное хорошее от нуля целое число, а т = 0, то для того чтобы числа р, дабы выполнялось равенство п = т*р не существует; в случае, если п = 0 и т = 0, то таких чисел р, для которых выполняется равенство п = т*р существует вечно довольно много. Так, частное от деления целого числа на нуль или не существует, или определяется не единственным образом. Исходя из этого говорят, что дробить на нуль запрещено, а выражение 0:0 не выяснено.
СВОЙСТВА и ЗАКОНЫ АРИФМЕТИЧЕСКИХ ОПЕРАЦИЙ НА МНОЖЕСТВЕ Z полностью совпадают с свойствами и аналогичными законами арифметических операций на множестве Z?.
СВОЙСТВА МНОЖЕСТВА ЦЕЛЫХ ЧИСЕЛ. СВОЙСТВА МНОЖЕСТВА ЦЕЛЫХ ЧИСЕЛ.
Теорема 8.22. (Теорема Архимеда). Для любых целых чисел а и в существует натуральное число п, что пв а.
Подтверждение. Разглядим число п = а’, т.е. п = а + 1. В силу теоремы 8.9 и следствия 2 имеем неравенства в 1 и п а. Почленно перемножая эти неравенства, возьмём пв а. Теорема доказана.
Теорема 8.23. (Принцип мельчайшего числа). Любое непустое подмножество множества целых чисел содержит мельчайшее число.
Подтверждение. Пускай множество М таково, что М I Z и
М ¹ ?. Разглядим два случая.
I. Множество М складывается из конечного числа элементов. В этом случае доказательно теоремы проводим способом математической индукции по числу элементов. В случае, если М складывается из одного элемента (М = {а}), то данный элемент и будет мельчайшим из чисел, входящих в М. Предположим, что теорема честна для множества М, содержащего некое конечное число элементов п. Иначе говоря думаем, что всякое множество М I Z, складывающееся из п элементов, содержит мельчайшее число. Пользуясь предположением, докажем, что множество М I Z, складывающееся из п + 1 элементов, кроме этого содержит мельчайшее число. Выберем произвольный I элемент аIМ и разглядим множество М? = М\{а}. Множество М? складывается из п элементов, соответственно по предположению в нем найдется мельчайшее число, которое обозначим через в. Так как аI М?, а вI М?, то а ¹ в, но тогда по теореме 8.10 из двух чисел а и в одно меньше другого. Мельчайшее из двух чисел а и возначим через с. Разумеется, что с есть мельчайшим числом в множестве М.
Итак, все условия способа математической индукции выполнены и справедливость теоремы для любого конечного подмножества доказана.
II. Пускай сейчас множество М складывается из нескончаемого числа элементов. Выберем любой элемент n из множества М. Число n разбивает множество М на два подмножества:
М? = {х/хIМ , х ? п}и М? = {х| хIМ х п }. Множество М? складывается из конечного числа элементов (их не более чем п + 1), соответственно по первой части теоремы, в нем содержится мельчайшее число, которое обозначим через т. Итак, для любого хIМ? , имеем т ? х. В частности, т ? п. Но тогда, учитывая определение множества М?, приходим к выводу, что мельчайшее число во всем множестве т . Теорема доказана.
Теорема 8.24. {Принцип наибольшего числа). В случае, если М — непустое подмножество множества целых чисел и существует такое число в, что для любого числа хI М выполняется неравенство х
Подтверждение теоремы подобно доказательству теоремы 8.23.
Теорема 8.25. {Свойство дискретности множества Z). Для любого
аI Z не существует целого числа п для того чтобы, что а п а’.
Подтверждение совершим способом от противного. Пускай существует такое п, что выполняются оба неравенства: а п и п а’. По определению отношения меньше существуют такие целые числа с? и с?, такие, что а + с? = п и п + с?= а’. Тогда а + (с? + с?) = а ‘ т.е. с? + с? = 1. Иначе,
с? ? 1 и с? ? 1, исходя из этого с? + с? ? 2. Пришли к несоответствию с допущением, значит, оно неверное. Теорема доказана.
Теорема 8.26. Множество целых чисел Z: а) нескончаемое; б) дискретное; в) линейно упорядоченное; г) счетное, д) в нем имеется мельчайшее число и нет наибольшего числа; е) в нем выполняются правила мельчайшего и наибольшего числа и свойство Архимеда.
Подтверждение, а) В множестве Zесть личные подмножества, каковые ему эквиваленты. К примеру, множество четных целых чисел есть подмножеством Zи ему эквивалентно, исходя из этого множество Zбесконечное; б) Свойство доказано в теореме 8.25; в) Свойство доказано в теореме 8.10; г) Свойство направляться из определения счетного множества: д) Свойство доказано в теореме 8.9 и следствиях нему; е) Свойство доказано в теоремах 8.23 и 8.24.
Теорема 8.35. Множество целых чисел Z: а) нескончаемое; б) дискретное; в) линейно упорядоченное; г) счетное, д) в нем нет солиднейшего и мельчайшего чисел.
Подтверждение фактически всех особенностей подобно доказательству особенностей множества натуральных чисел N и Z?.
ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ЦЕЛЫХ ЧИСЕЛ. Каждому целому числу х ставится в соответствие точка М прямой, отстоящая от фиксированной точки 0 на IхI единиц и расположенная на правом луче, в случае, если х — положительное число, и на левом, — в случае, если х — отрицательное число. Число х, соответствующее точке М, именуется координатой данной точки. Тот факт, что точка М имеет координату х, записывается М(х). Изображение целых чисел посредством точек прямой разрешает задавать не только длины отрезков, но и показывать их направление. Следовательно, геометрически целое число – это направленный отрезок, лежащий на прямой и выходящий из фиксированной точки 0.
Геометрически сложение чисел х и у свидетельствует перенос точки М(х) на IуI единиц вправо, в случае, если у 0, и влево, в случае, если у 0 х + у х, а при у 0 х + у х.