— она постулирует возможность существования плоскости (а при переходе к количеству — пространства) с разной метрикой в ортогональных направлениях. Следствие анизотропии напряженности потенциальной бесконечности.
— она постулирует возможность долгого периода перемещения линии. Другими словами постулирует существование времени, которое отсутствует в статической геометрии по определению, и наличие потенциальной бесконечности.
Все четыре неявных постулата относятся не к актуальной бесконечности, а к бесконечности потенциальной. Их наличие говорит о том, что плоскость, на которую нанесены геометрические элементы (в линии и частности точки), имеет неоднородную напряженность поверхности (независимо от того, понимаем ли мы это либо нет, но в структуре уравнений существует память числа, состояния и фигуры пространства, каковые проявляются в итогах ответа). И эта неоднородность обусловливает искривление прямой, движущейся на протяжении существующей (?) линии как в одну сторону от точки, так и в другую сторону от нее. (Кстати, постулируемая в теореме прямая на плоскости может оказаться лишь в отечественном воображении, а движутся, оставляя следы, точки.) Темперамент же искривления зависит от того, какие конкретно граничные условия и в каком направлении пространства определяют перемещение точки.
Изменение напряженности пространства искривляет прямую движущуюся на бесконечность. Перемещение же на бесконечности обусловливает возможность формулировки нескольких вариантов пятой теоремы Евклида. Эти формулировки смогут задействовать как свойства статики, так и динамики, что и проявилось в определениях Лобачевского и Римана при рассмотрении пятой теоремы Евклида. Новые определения стали базами так называемых «неевклидовых» геометрий.
Краткий анализ баз геометрий
Лобачевского и Римана
В начале, ХIХ века Н. Лобачевский, пробуя доказать параллельность прямых способом от противного, предположил:
«Через точку, лежащую вне прямой, возможно совершить нескончаемое множество прямых, параллельных первой».
Основываясь на этом определении, он вывел десятки логически корректных теорем, базирующихся на особенностях актуальной и потенциальной бесконечности, каковые в собственном развитии и обусловили появление первой неевклидовой (??-Авт.) геометрии.
Разглядим кое-какие особенности неэвклидовой геометрии. У него, как и у Евклида, имеется точка М и прямая а, актуальной бесконечности. Но граничные условия поменяны: существует множество «прямых» b, c, d,…проходящих через точку М параллельно прямой а (рис. 20). Лобачевский постулирует, что к прямой а, через точку М возможно совершить две прямые b и с так, что они не пересекаются с прямой а. Ясно, что прямые, располагающиеся между предельными b и с, в a тем более не пересекут а. Угол g между отрезком МN и прямой с Лобачевский именует углом параллельности g p.
Неэвклидова геометрия владеет следующими изюминками:
— в отличие от Евклида расстояние между параллельными непостоянно. В одном направлении асимптотически значительно уменьшается, в другом — возрастает до бесконечности;
 Рис. 20.  с  a M  d b b g а N |
— движущаяся прямая такой не есть, и потому названа Лобачевским эквидистантой. И это главное отклонение от евклидова пространства, не приобретающее геометрического объяснения. Нарушение прямолинейности возможно растолковать лишь анизотропией пространства (плоскости), в которой прямая движется;
— угол параллельности g изменяется в зависимости от расстояния точки М до прямой а. При удалении от прямой он значительно уменьшается, и в пределе, в то время, когда М находится на бесконечности, g ® 0. Прямая как бы может проходить через М под прямым углом к а, но при перемещении искривляется и, сближаясь с прямой а, «уходит» на параллельность и в бесконечности нигде с ней не пересекается. А это — показатель прямой и взаимного отталкивания точки, т.е. показатель свойства потенциальной бесконечности;
— в случае, если около асимптоты а, как оси, вращать эквидистанту b либо с, то получающаяся фигура именуется псевдосферой отрицательной кривизны (??- Авт.), а эквидистанта делается геодезической на ней.
самоё известное отличительная особенность и свойство псевдосферы неэвклидовой геометрии в том, что сумма углов треугольника на поверхности псевдосферы в любой момент 2p и по мере повышения треугольника — значительно уменьшается. Исходя из этого, при неизменной метрике, существует однозначная зависимость между углами треугольника и сторонами (в метрике Евклида). И как не существует сколь угодно громадных треугольников, так и не существует равенства и подобия треугольников по всей площади псевдосферы.
Все особенности неэвклидовой геометрии проявляются благодаря отступления от статичности актуальной бесконечности и применения в качестве граничных условий особенностей потенциальной бесконечности и первым делом перемещения. Потому, что эти особенности вводятся неявным образом, темперамент их действия на статическую геометрию выясняется не раскрытым и особенности неэвклидовой геометрии не растолкованы, а сама геометрия была организована в рамках статики и потому не может быть названа неевклидовой геометрией. Евклидова геометрия – это статическая геометрия. Неевклидова – противоположная статической, динамическая (физическая) геометрия.
Подобное случилось и с геометрией Римана. Потому, что эта геометрия есть базисом самая популярной гравитационной теории, остановимся на ней пара подробнее.
В первую очередь напомним, что она складывается из двух неравнозначных как следует и искусственно соединенных (соглашение) частей. Одна — строение сферической (эллиптической) геометрии с применением многомерных многообразий, вторая — математический аппарат описания геометрии двумерных кривых поверхностей. Последний был создан Гауссом для евклидовых поверхностей и предусматривал изучение их двумя методами:
— задавая уравнение поверхности в трехмерном пространстве (взаимоотношения между поверхностными точками довольно некоей пространственной совокупности координат);
— применяя свойства поверхности в двумерной совокупности координат с осями на ней.
Изучая геометрические особенности сферы, каждую точку на поверхности определяют двумя координатами — широтой и долготой. Совокупность измеренных на поверхности и характеризующих ее соотношений и именуется внутренней геометрией поверхности.
К этим соотношениям относятся: протяженность отрезков либо линий между некоторыми парами точек, угол между линиями, уравнение геодезических, площадь поверхности либо ее кривизна в разных точках. Отображение бесконечно малого отрезка через разность координат дает метрику поверхности и в общей форме имеет форму:
dS2 = aikgikdxidxk ; i = k = 1, 2.
В данной формуле
ds — бесконечно малый отрезок между точками xi , xi + dxi,
dxi, dxk — дифференциалы координат,
gik — коэффициенты связи ds c dxi; dxk. Они, в общем случае зависящие от координат, переменные. Зная эту зависимость возможно выяснить длину отрезков, углы между линиями, площади, ограниченные контурами на поверхностях. По трем функциям коэффициентов определяется инвариантная черта поверхности — ее кривизна в каждой точке. (Она инвариантна, потому, что изменяется при изгибах без растяжения).
Мерой кривизны поверхности делается степень ее отклонения в некоей точке от касательной плоскости. В пределах поверхности устанавливаются только определенные зависимости между метрическими коэффициентами gik и их производными по координатам. Они-то и определяют отклонение от плоскости либо кривизну.
Считается, что римановы плоскости кроме этого имеют евклидову мерность. А исходя из этого на них кривизна, зависящая от gik и их производных, равна нулю. Искривленная поверхность имеет довольно плоскости Евклида метрику неевклидову (рис.21).
Неевклидова метрика определяется конкретно соотнесением с положением поверхности, а потому есть субъективной оценкой кривизны. К примеру, протяженность отрезка АоА, определенная относительно линии а, будет равна А¢оА¢, что намного меньше АоА, (А¢оА¢ АоА). А его же протяженность, отнесенная к линии b, будет ненамного меньше АоА и намного больше А¢оА¢. (АоА А¢¢оА¢¢ А¢оА¢). И исходя из этого постоянно следует оговариваться, довольно какой плоскости определяется кривизна.
 Рис. 21. а A Ao¢ Bo¢ A¢ Ao Ao¢¢ A¢¢ |
Основное, но, в том, что процедура соизмерения кривизны поверхности (либо количества) производится на довольно не родственную себе поверхность и оторвана от процесса образования самой кривизны. А потому не имеет возможности принимать во внимание корректной.
Гауссова теория кривизны была дополнена Риманом обобщенными понятиями многомерных многообразий. (Многократно протяженных размеров, неким аналогом n-мерного геометрического пространства, потому, что понятие «протяженность» у Римана отображает длину). Так, к примеру, в случае, если поверхность — двукратно протяженная величина, то пространство — трехкратно протяженная величина и т.д. Другими словами поверхность, и пространство у Римана как следует не различаются. Так, свойства мерности оказываются однокачественными, а сами мерности между собой тождественными, а потому получается, что связи между единичными мерностями отсутствуют и лишь количество протяженностей (? ? Авт.) определяет кратность геометрического пространства. Постулирование многомерных однокачественных многообразий разрешило конкретно перенести на «искривленное» трехмерное пространство способы описания двумерных поверхностей с их метрикой, узаконив тем самым отсутствие связи между мерностями. Это еще одна громадная некорректность геометрии Римана.
Не смотря на то, что данный подход к описанию пространства обусловливает построение частных неевклидовых пространств, и создание теории произвольно искривленных поверхностей. Его некорректности стали причиной выделению трех, не существующих в природе, типов пространств постоянной кривизны (все римановы пространства): пространства Лобачевского — отрицательной кривизны (сумма углов треугольника в нем 2p). Все пространства математически не сводимы друг к другу и имеют основанием разные определения одной и той же пятой теоремы Евклида. В геометрии Римана она сформулирована как отрицание постулата Лобачевского:
“Через точку, лежащую вне прямой, нереально совершить ни одной прямой, параллельной первой”.
Формулировки теоремы о параллельных Лобачевского и Римана, не смотря на то, что и приводят к построению разных геометрий, имеют следующие неспециализированные изюминки:
— они постулируют точки и равнозначность прямой;
— они постулируют наличие изотропного и однородного пространства как недалеко от точки, так и на бесконечности;
— они неявно постулируют наличие отрезка второй прямой, нескончаемой в сторону, противоположную перемещению и, следовательно, уже параллельную существующей;
— они постулируют возможность прямолинейного перемещения линии на бесконечность, которое, однако, по непонятной обстоятельству, оказывается не прямолинейным;
— они переносят математическое перемещение как преобразование конечных количественных размеров на перемещение нескончаемое, не имеющее количественного отображения и благодаря этого — неизвестное, неосуществимое для математических преобразований;
— перенос математического преобразования на перемещение на бесконечность в формальных граничных условиях и приводит к искривлению “прямых”;
— невозможность математического преобразования перемещения прямой линии через точку на бесконечность говорит о том, что теоремы Лобачевского и Римана обрисовывают механическое перемещение точки, а образованные на их базе геометрии не являются статическими.
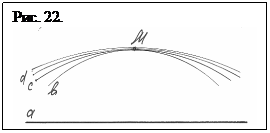
На рис. 22 схематично изображены римановы “прямые”, не параллельные прямой а. Причем точка М, находящеяся в собствености кривым, не выделена и равнозначна всем точкам на этих кривых. Другими словами М есть точкой не римановой, а евклидовой геометрии (не образует напряженности пространства). Но в случае, если прямая в движении на протяжении второй прямой, искривилась, то это может случиться лишь в том случае, в то время, когда она движется в пространстве изменяемой напряженности и потому ни при каких обстоятельствах не пересечется с прямой, подходя к ней все ближе и ближе, на протяжении которой она движется. Исходя из этого, в случае, если любую из кривых b, с, либо d вращать около прямой, а риманова пространства, то образуется незамкнутая эллиптическая поверхность (у полюсов на протяжении а останутся “дыры”). Она как бы замыкает в себе некий количество, отделяя риманово пространство от внешнего не “пространства” и создавая “дырявую” сферу-пространство, поверхность конечной площади отграниченную “дырами” от прямой а. Такая фигура не смотря на то, что и есть римановой поверхностью, но имеет внутреннюю плотность и не есть ни эллипсом, ни сферой и не имеет постоянного количества.
Разглядим, к примеру, основанное на получении вращением римановых кривых утверждение о том, что все прямые на римановой поверхности пересекаются. Оно основывается не на изучении поведения “прямых” при образовании римановой сферы, а на гауссовой теории кривизны. Наряду с этим забывается, что появившаяся при вращении “сфера” не замкнута, имеет в себя ось с двумя полюсами и неоднородное пространство. Причем прямая есть атрибутами образовавшего пространства. Ее нереально «выдернуть» никакими преобразованиями, потому что это сходу поменяет («уберет») напряженность, да и форму пространства. (У Евклида одна ли прямая, обе ли параллельные либо образуемая ими при вращении цилиндрическая поверхность никак не изменяют состояние пространства, а потому допустимо вольное обращение с каждым элементом фигуры.)
Незамкнутость римановой сферы (как и псевдосферы Лобачевского) говорит о том, что обе геометрии геометриями как таковыми не являются. При их формировании смешаны евклидовы и неевклидовы свойства. Они имеется лишь некая часть более неспециализированной геометрии и потому на их базе нереально выстроить (не нарушая законов статической геометрии) ни одной пространственной фигуры, кроме того таковой простой, как сфера.
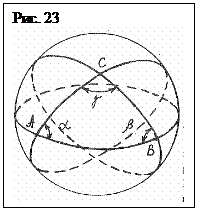
Для римановой сферы базовой прямой всех параллельных довольно ее линий есть ось-прямая а (см. рис. 20.). А параллельные, геодезические римановой геометрии, проходят от одной оси к второй и нигде не пересекаются между собой. Утверждение типа: «… понятие параллельных линий в сферической (римановой – Авт.) геометрии по большому счету теряет суть, потому что каждая дуга громадного круга, проходящая через точку С, лежащую на линии АВ, непременно пересекает АВ, причем в двух точках. Из рис. 23 кроме этого видно, что сумма углов треугольника АВС, образованного пересечением трех дуг громадного круга, в любой момент больше 180о» [22] — не обосновано и базируется на путанице особенностей евклидовой и римановой геометрий.
Выше упоминалось, что выстроить сферу в римановой геометрии нереально, что сфера строится лишь в геометрии Евклида и перенесение особенностей одной геометрии на другую некорректно. К примеру, дуги громадного круга не наличествуют в геометрии Римана и потому не пересекаются на ней. Второй пример. На сфере Евклида метричность неизменна, а на сфере Римана изменяется в зависимости от напряженности пространства (само собой разумеется по сравнению со статичностью), а потому ориентация на сумму углов треугольника некорректна и сравнение данной суммы со 180о по большому счету ведет к парадоксу. Продемонстрируем его.
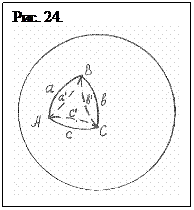
Предположим, что из узкой прозрачной резиновой пленки склеена и надута сфера-шар (рис. 24.). На поверхности шара нанесены три точки А, В, и С, соединенные прямыми а, b, с. Появившийся треугольник АВС на сфере хорошей кривизны имеет, в соответствии с геометрии Римана, сумму углов 2p.
Сейчас, в случае, если мы окажемся в шара, в сфере отрицательной кривизны то, в соответствии с той же геометрией Лобачевского и теорией кривизны, сумма углов треугольника со сторонами а¢, b¢, с¢ (изображенного на рис. 24 пунктиром.) будет составлять 2p.
Появляются вопросы: Какой из этих треугольников отображает настоящее искривление сферы? И по какой причине:
[( 2p) + ( 2p)]/2 = 2p ?
Предстоящее раздувание шара будет увеличивать сумму углов наружного треугольника, и уменьшать ту же сумму внутреннего, оставляя итог ответа формулы неизменным.
Данный парадокс появляется по причине того, что риманова кривизна пространства не характеризует конкретно пространство. Эта кривизна позвана произвольным переносом двумерного измерения — плоскости, на трехмерное измерение — количество. Перенос осуществлялся исходя из предположения, что мерности пространства не имеют качеств, и некорректен уже по причине того, что плоскость характеризуется квадратом протяженности, а количество пространства — кубом.
2.6. Что скрывают неевклидовы геометрии?
Не смотря на то, что первыми авторами неевклидовых геометрий были Лобачевский, Больяйя, идеологию этих геометрий высказал и стал автором одной из них (эллиптической) Риман. Приступая к рассмотрению статических геометрий, возвратимся к идеям, изложенным в его известном формуляре [4]. Напомним, что Риман исходил из того, что существуют какие-то условия либо эти, априорно заложенные в понятие пространство. Он применял, в качестве опоры, понятие «протяженность», полагая его аналогом лишь геометрического понятия длины и не подмечая заложенных в качественности и протяжённость телесности. К тому же заложенных не априорно, а как обобщенные характеристики множества настоящих вещественных предметов. Другими словами понятия, сформировавшегося многовековым опытом человечества. Конкретно качественности понятия и игнорирование телесности «протяженность» и обусловило авторам «неевклидовых» геометрий непонимание подлинного значения проделанной ими работы и того результата, что стал называться «неевклидовы геометрии».
Потому, что исходным неевклидовых геометрий есть постулат о параллельных, разглядим те трансформации, каковые изменяют суть теоремы Евклида. Как пример будем ориентироваться на краткое подтверждение истинности теоремы Лобачевского, изложенное М. Клайном в работе [3], для того, чтобы продемонстрировать, как неявным образом, отражается на понимании данной теоремы пропущенные телесность и качественность протяженности:
«Пускай задана точка и прямая АВ вне ее Р(рис. 25). Тогда все прямые, проходящие через точку Р, распадаются по отношению к прямой АВ на два класса: класс прямых, пересекающих АВ, и класс прямых, каковые АВ не пересекают. К числу последних принадлежат две прямые р и q, разделяющие отечественные два класса прямых. Сообщённому возможно придать более надежный суть. В случае, если Р — точка, находящаяся от прямой АВ на расстоянии Л (Л — протяженность перпендикуляра РD, опущенного из точки Р на прямую АВ), то существует острый угол a, таковой, что все прямые, составляющие с перпендикуляром РD угол, меньший a, пересекаются с прямой АВ, а все прямые, составляющие с РD угол, больший либо равный a, не пересекаются с АВ. Две прямые р и q, образующие с РD угол a, именуются параллельными по Лобачевскому прямой АВ, а угол a = (a(Л)) именуется углом параллельности (отвечающим отрезку PD = Л). Прямые, проходящие через точку Р (хорошие от параллельных прямых р и q) и не пересекающиеся с прямой АВ, именуются расходящимися с АВ прямыми (либо сверхпараллельными ей; в евклидовой геометрии они были параллельны прямой АВ). В случае, если осознавать параллелизм по Евклиду, т.е. именовать параллельными каждые две прямые, каковые лежат в одной плоскости и не пересекаются между собой, то в неэвклидовой геометрии через точку Р проходит вечно довольно много прямых, параллельных АВ.
Рис. 25.
Р
a a
р g
Л
А D В 
После этого Лобачевский обосновывает пара главных теорем. В случае, если угол a равен p/2, то мы приходим к евклидовой теореме о параллельных. В случае, если угол a острый, то при неограниченном росте Л, он монотонно убывает и пытается к нулю. Сумма углов треугольника в любой момент меньше 180о и пытается к 180о, в то время, когда площадь треугольника неограниченно убывает (п ?ж курсив отечественный – Авт.). Два аналогичных треугольника, имеющих однообразные углы, в любой момент конгруэнтны”.
Тут крайне важно представить поведение “прямых” в то время, когда при перемещении прямой в одном из направлений прямая-луч Л, начинает неограниченно возрастать, и угол a монотонно убывает в рвении к нулю. Оно, это возрастание, говорит о повороте “прямых” (изгибании) р либо q в рвении появляться перпендикуляром к АВ. Но, по логике вещей, при удлинении, Л, «прямая» р обязана передвигаться оставаясь параллельной сама себе. И если она поворачивается (изгибается), то появляется вопрос: Какой же механизм снабжает данный поворот? Нам нигде не виделось объяснение этого механизма и появляющихся из рвения к повороту вопросов: Какая математическая операция заставляет, при удлинении прямой искривляться и выставлять р в оппозиционеров прямой АВ? А при перемещении в противоположную сторону к А — убывании, искривляясь уходить на параллельность? Считать, что это происходит случайно, не приходится, потому, что такая же процедурас точностью напротив повторяется и в римановой геометрии. Либо за ним кроется не геометрическая, а физическая составляющая? Та составляющая, которая еще не замечается, и которую снабжает телесность понятия «протяженность», заложенная в математических формулах и проявляющая себя кроме воли не подозревающих об этом ученых. И, как сказал Герц, формулы выясняются умнее собственных разработчиков. Давайте разберемся в этом как следует.
В неевклидовых полудинамических геометриях центр плотности как бы отсутствует (о возможности его существования не имеется явной информации) не смотря на то, что пространство владеет изменяемой плотностью, и его плотностные функции неявно покупают ближайшая к N равнозначная по рангу точка М на «нескончаемой» линии. Точка же N преобразовывается, так, в точку «падающую» на М. Между ними «создается» скрытое в математической формализации анизотропное поле напряженности, при помощи которого они взаимодействуют между собой. Для N как бы отсутствует прямая, на которой находится точка М. Эта анизотропия (изображена штрихами на рис. 26.), обусловливает точке N, движущейся совместно с М в пространстве изменяемой плотности, возможность образовывать фигуры геометрий Лобачевского, или геометрии Римана. Это наиболее значимая изюминка теорем о параллельных «неевклидовых» статических геометрий — одновременное неявное перемещение двух взаимодействующих точек однообразного ранга в анизотропном пространстве на бесконечность.
(Для описания перемещения точки в бесконечности используют предлог «в», предполагая прямую направленность перемещения. Но заблаговременно нереально знать в каком пространстве оно будет происходить. И потому, неизвестно останется ли направление перемещения прямолинейным либо искривится в неизвестном направлении. Исходя из этого, для описания нескончаемого перемещения нами употребляется выражение «на бесконечность».)
Конкретно анизотропия пространства и обусловливает точкам-пилотам искривление траектории, проявляющееся как искривление линии. А так как возможности искривления траектории перемещения точки М ограничены “нескончаемой” статической прямой, на протяжении которой она движется, то точка N и выписывает фигуры «неевклидовых» геометрий в рамках заданных граничных условий. Потому, что “сотрудничество” точек М и N имеет темперамент притяжения либо отталкивания, то это сотрудничество возможно отображено на рисунке при помощи соединения точек М и N линией-лучом МN (рис. 26).
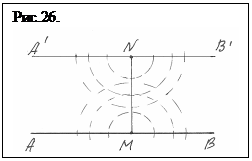Изменение “длины” луча, обусловленное перемещением одной либо обеих точек, и приводит к возникновению фигур той либо второй геометрий. Исходя из этого линия-луч МN возможно названа образующей и обозначена буквой Л. Линия (условная), соединяющая две движущиеся в некотором роде плотностные точки, именуется образующим лучом Л либо образующим. Так, в случае, если одна из точек неподвижна на плоскости, а вторая, не меняя расстояния до первой, обрисовывает в движении верный круг, то образующий луч с этими особенностями в геометрии именуется радиусом. А геометрии, в которых перемещение одних фигур ограничены статическими конструктами вторых, смогут быть названы не неевклидовыми геометриями.
Возвратимся к рис. 25 и напомним, что в математических уравнениях для точки Р прямая АВ не «существует». Она взаимодействует лишь с точкой D, перемещение которой по условиям задачи, происходит по прямой АВ. Разглядим как двигаются в противоположных направлениях “прямые” р и q при перемещении на протяжении прямой АВ. Отметим штрихами траекторию их перемещения на бесконечность. И заметим, что, к примеру, точка Р при перемещении (думаем, что движется сама точка Р, оставляя за собой след-кривую линию р) в направлении В монотонно возрастает удаляясь от АВ и на бесконечности касательная от следа в точке Р’ на АВ опускается фактически под углом в 90о к АВ, т.е перпендикулярно, а сама траектория РР¢ по собственной кривизне выясняется правой ветвью полуэллипса (рис. 27). Касательная к ней, — перпендикуляр к АВ делается лучом Л¢ соединяющим крайнюю точку кривой РР¢ с передвинувшейся к этому месту точкой D¢, потому, что сама точка Р движется не относительно прямой АВ, а в оппозиции с точкой D, движущейся вместе с Р на протяжении прямой АВ. И в ходе совместного перемещения луч-перпендикуляр Р¢D¢ — Л¢, или удлиняется при перемещении в одном направлении или сокращается при перемещении в противоположном направлении.И, следовательно, поведение прямой р определяется направлением ее перемещения. Данный момент, обусловленный скрытым сотрудничеством точек Р и D, и есть решающим для понимания сути «неевклидовых» геометрий.
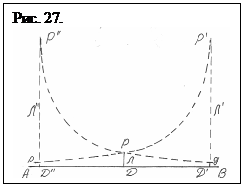При перемещении Р в направлении А с тем же трансформацией скорости появляется второй след-кривая РР¢¢, образуя левую ветвь полуэллипса. И в случае, если их разглядывать совместно, то можно подчернуть, что обе полуветви, соединенные точкой Р, образуют полуэллипс Р¢¢РР¢ с неявным центром О между ними. К тому же, к примеру, в точке D¢, луч Л¢ преобразовывается в перпендикуляр оставаясь касательной Р¢D¢, и прямая АВ для правой полуоси практически прерывается (потому, что прямая АВ не “существует” для правой полуветви РP¢), выясняясь практически не нескончаемой, а неизвестной, и зависящей от кривизны траектории РР¢, ограниченной в сторону В. И потому протяженность ее правой ветви определяется подъемом точки Р, а, следовательно, и направлением, в котором она движется. Но для субъекта, начертившего линию АВ, она в направлении В длится вечно.