Элементы орбиты — шесть размеров, определяющих размеры и форму орбиты небесного тела, ее положение в пространстве, и положение самого небесного тела на орбите. Элементы орбиты обрисовывают закон перемещения небесного тела: зная их, возможно вычислить, в какой точке пространства находится небесное тело в любой- заданный момент времени.
размеры и Форма орбиты определяются громадной полуосью орбиты (а = ОП) и эксцентриситетом орбиты е:
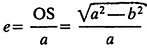
где b — малая полуось орбиты. Для эллиптической орбиты значения эксцентриситета заключены в пределах: 0?е1 орбита гиперболическая (см. Орбиты небесных тел).
Ориентация орбиты в пространстве определяется довольно некоей плоскости, принятой за главную. Для планет, других тел и комет Нашей системы таковой плоскостью помогает плоскость эклиптики. Положение плоскости орбиты задается двумя элементами орбиты: долготой восходящего узла ? и наклоном (наклонением) орбиты і. Долгота восходящего узла — это угол при Солнце между линией эклиптики плоскостей и пересечения орбиты и направлением на точку весеннего равноденствия. Угол отсчитывается на протяжении эклиптики от точки весеннего равноденствия ? по часовой стрелке до восходящего узла орбиты ?, т. е. той точки, в которой тело пересекает эклиптику, переходя из южной полусферы в северную. (Противоположная точка именуется нисходящим узлом, а линия, соединяющая узлы, — линией узлов.) Долгота восходящего узла может иметь значения от 0 до 360°.
При изучении перемещения неестественных спутников Почвы в качестве главной берут плоскость экватора; в этом случае линия узлов — это линия небесного плоскостей экватора и пересечения орбиты. Ее положение определяется прямым восхождением восходящего узла ??, отсчитываемого от точки весеннего равноденствия на протяжении экватора (см. Небесная сфера).
Положение орбиты в плоскости Q определяется доводом перигелия ?, воображающим собой угловое расстояние перигелия орбиты от восходящего узла: ? = ?П. Довод перигелия отсчитывается в плоскости орбиты в направлении перемещения небесного тела и может иметь каждые значения от 0 до 360°. Для неестественных спутников Почвы данный элемент орбиты именуется доводом перигея.
В качестве шестого элемента, определяющего положение небесного тела на орбите в какой-нибудь определенный момент времени, применяют момент прохождения через перигелий То. Положение тела на орбите в каждый момент определяется посредством законов Кеплера. Угол при Солнце, отсчитанный от направления на перигелий до направления на тело, именуется подлинной аномалией у. Подлинная аномалия при перемещении тела по орбите изменяется неравномерно; в соответствии со вторым законом Кеплера тело движется стремительнее около перигелия П и медленнее — у афелия А. Подлинную аномалию вычисляют по известным формулам посредством запасном величины, именуемой средней аномалией М. Средняя аномалия изменяется равномерно, причем она равна 0 и 180° в один момент с подлинной аномалией (т. е. фиктивная точка, определяющая среднюю аномалию, проходит через афелий и перигелий в тот же момент, что и настоящее тело).
Среднюю аномалию М0 тела в эру (т. е. в некий заданный момент времени, к примеру в начале заданных дней) применяют довольно часто вместо шестого элемента Т0. Время от времени вместо этого элемента задают T? — момент прохождения тела через восходящий узел орбиты.
При известной массе центрального тела громадная полуось орбиты ? конкретно связана со средним перемещением n тела по орбите и периодом обращения Р. Эти размеры смогут задаваться в качестве одного из элементов орбиты вместо ?.
Элементы орбиты постоянны лишь при задачи двух тел (см. Небесная механика). В случае, если же на перемещение тела влияет притяжение третьих тел либо какие-либо иные силы (к примеру, сопротивление воздуха при неестественных спутников Почвы), то элементы орбиты непрерывно медлительно изменяются.
В этом случае понятие периода обращения получает пара значений, в зависимости от того, довольно какой точки он отсчитывается. Так, полный период обращения, отсчитанный относительно направления на ту либо иную звезду, именуется сидерическим периодом. В случае, если период отсчитывается относительно перигелия, то он носит название аномалистического периода; в случае, если довольно восходящего узла, то наименование драконического периода. При невозмущенного (кеплеровского) перемещения все эти периоды имеют однообразное значение; при возмущенном перемещении они смогут значительно различаться.