ГРАФИКОВ
7.1. Изучение посредством 1 – й производной.
Показатель монотонности функции
ТЕОРЕМА 1 В случае, если функция дифференцируема на
промежутке и на
, то функция не убывает (не воз –
растает) на промежутке .
Подтверждение. Заберём две точки , такие что . Тогда на отрезке выполняются все условия теоремы Лагранжа, в соответствии с которой приобретаем
Тогда, в случае, если на , то ; в случае, если на , то . Теорема доказана.
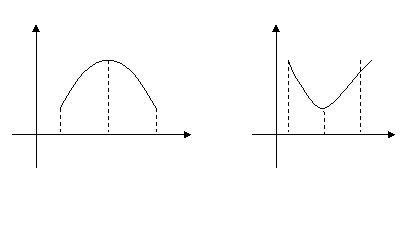
Точка именуется точкой строгого локального макси -мума (минимума) функции , в случае, если для всех из некоей d — окрестности точки выполняется неравенство . При . (см. рис 1)
Y y
maxx
minx
O O
(рис. 1)
Локальный максимум ( ) и локальный минимум ( ) объединяют неспециализированным заглавием локальный экстремум.
ТЕОРЕМА 2 (нужное условие локального экстремума)
В случае, если функция имеет в точке локаль –
ный экстремум и дифференцируема в данной
точке, то .
Подтверждение. Так как в точке функция имеет ло -кальный экстремум, то существует промежуток, , в котором значение есть громаднейшим либо наимень- шим, а тогда, по теореме Ферма, в данной точке производная равна 0., т.е. .
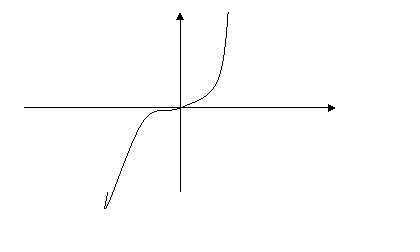
Условие — это нужное но не достаточное условие экстремума. Время от времени точки, в которых , именуют критическими точками , либо точками вероятного экстремума функции . В этих точках экстремум возможно либо не быть, К примеру, в случае, если разглядеть функцию . Её производная в точке . Но по виду графика, можем выяснить, что в данной точке функция не имеет экстремума. (см. рис 2)
Y
- x
ЗАМЕЧАНИЕ. В случае, если в точке производная не су -щеествует, но сама точка входит в область определения функции , то точка кроме этого есть критической точ -кой функции .
ТЕОРЕМА 3 (достаточное условие экстремума) Пускай функ-
ция дифференцируема в некоей d — ок –
рестности критической точки , тогда, в случае, если в
данной точке производная меняет символ с на
, то в точке функция имеет локальный
минимум, а вдруг в точке символ производной
изменяется с на , то в точке функ –
ция имеет локальный максимум.
ПРИМЕРЫ. Выстроим графики функций при помощи производной 1-го порядка.
1. 
.
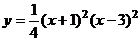Эта функция выяснена для всех х, принимает она лишь хорошие значения. при .
Отыщем производную это1 функции:
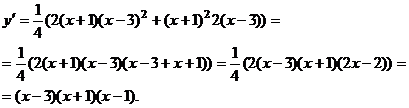
при Это критические точки функции. Выстроим числовую ось
— -1 + 1 — 3 +
min max min
, 
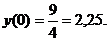
Изучение посредством первой производной завершено. Мы узнали, что график имеет две точки локального минимума и одну точку локального максимума. Нашли возрастания функции и промежутки убывания. Нашли точки пересечения с осями координат. Осталось выстроить график.
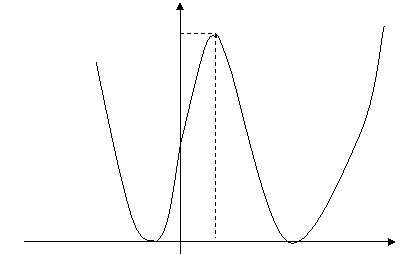Y
2,25
-1 O 1 3 x
2. .
Эта функция выяснена для всех и принимает каждые значения.. при Отыщем её производную:
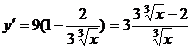. Критическими точками являются:
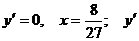не существует, . Выстроим числовую ось
+ 0 — + х
Определим значения функции в критических точках ,
.
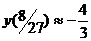Выстроим график
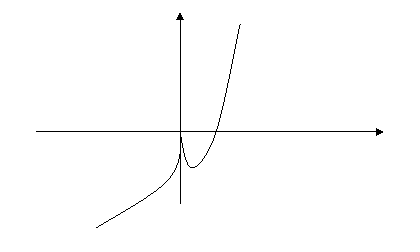
У
О 1 х
ЗАМЕЧАНИЕ. В случае, если в точке производная не существует, то в данной точке график функции имеет вертикальную касательную ( , если точка входит в область определения)
7.2. точки перегиба и Направление выпуклости графика функции.
Пускай функция дифференцируема на промежутке . Тогда существует касательная к графику данной функции в любой точке , причём эта касательная не параллельны оси , так как её угловой коэффициент, равный , конечен.
О п р е д е л е н и е 1.. Будем говорить, что график функции имеет выпуклость, направленную вниз (либо вогнутость) в случае, если расположен не ниже любой собственной касательной в разглядываемом промежутке, подобно, график имеет выпуклость, направленную вверх (либо легко выпуклость) если он находится не выше любой собственной касательной. (см. рис.)
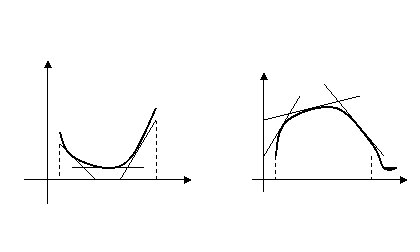
У у
Вверх
Вниз
O a b x O a b x
ТЕОРЕМА 1. В случае, если функция имеет на промежутке
вторую производную и
во всех точках проме –
ужасна , то график функции име –
ет на этом промежутке выпуклость, направлен –
ную вниз (вверх).
Подтверждение. Требуется продемонстрировать, что график функции находится не ниже (не выше) любой касательной, совершённой в произвольной точке графика функции. Запишем уравнение данной касательной, обозначив её текущую ординату через . (1)
Напишем разложение функции в окрестности точки по формуле Тейлора при
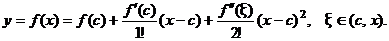(2)
Вычитая равенство (1) из равенства (2), возьмём
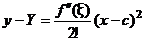. (3)
Тогда, в случае, если , то и график функции расположен не ниже (не выше) любой касательной.
О п р е д е л е н и е 2. Точка именуется точкой перегиба функции , в случае, если в точке ,, в случае, если в данной точке график функции меняет направление выпуклости.
ТЕОРЕМА 2 (Нужное условие выпуклости). Пускай гра-
фик функции имеет перегиб в точке
и пускай функция имеет
в точке постоянную вторую производную.
Тогда .
Эта теорема направляться из определения точки перегиба — точке перегиба изменяется вторая производная и направление выпуклости меняет символ в данной точке. А так как вторая производная постоянна в данной точке, то она обращается в ноль в токе ..
ЗАМЕЧАНИЕ 1. В случае, если , то достаточным условием точки перегиба в точке есть смена символа второй производной в данной точке.
ЗАМЕЧАНИЕ 2. В точке перегиба касательная пересекает график функции, поскольку с одной стороны график функции находится выше касательной, а с другой — выше, т.е. перегибается через неё. (См. рис.)
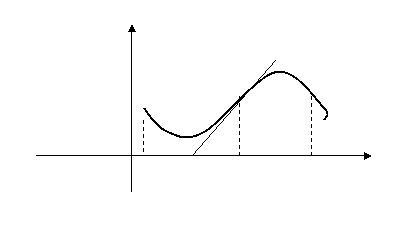
У
M
O a b x
ЗАМЕЧАНИЕ 3. В случае, если — точка максимума функции , то , в случае, если — точка минимума, то . Это ещё одно достаточное условие экстремума функции.
7.2. Асимптоты графика функции.
При изучении поведения функции на бесконечности, т.е. при , либо вблизи точек разрыва 2 – го рода довольно часто выясняется, что график функции сколь угодно близко приближается к той либо другой прямой. Такие прямые именуются асимптотами.
Существуют три вида асимптот: вертикальные, горизонтальные и наклонные.
О п р е д е л е н и е 1. Прямая именуется вертикальной асимптотой графика функции , в случае, если хотя бы одно из предельных значений либо равняется либо .
О п р е д е л е н и е 2. Прямая именуется горизон- тальной асимптотой графика функции при либо , в случае, если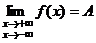 
.
О п р е д е л е н и е 3. Прямая ( ) называ- ется наклонной асимптотой графика функции при , в случае, если функцию возможно представить в виде , где при либо .
Наряду с этим числа и , задающие уравнение наклонной асимптоты находятся по следующим формулами:
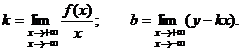
Фактически целесообразно искать асимптоты в такой последовательности: 1) вертикальные асимптоты (в случае, если имеется точки разрыва 2 – го рода 2) наклонные асимптоты. Горизонтальная асимптота — частный случай наклонной асимптоты при либо . Горизонтальная асимптота — это частный случай наклонной асимптоты при либо , , если .
ЗАМЕЧАНИЕ 1. В случае, если хотя бы одно из чисел или , или , то график функции не имеет ни наклонной ни горизонтальной асимптоты.
ЗАМЕЧАНИЕ 2. график функции не имеет возможности иметь больше двух наклонных асимптот.
ПРИМЕР. Отыскать асимптоты графика функции
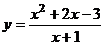и выстроить её график.
В область определения данной функции не входит точка . Отыщем в данной точке односторонние пределы.
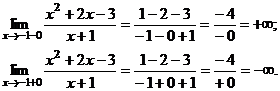
Следовательно, — вертикальная асимптота графика.
Отыщем наклонную асимптоту: .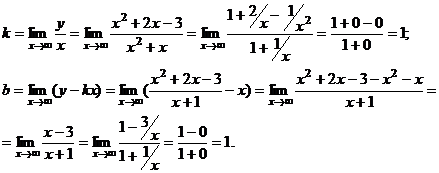 
Так, наклонная асимптота имеет уравнение
Дабы поточнее выстроить график, отыщем ещё нули функции: в случае, если , то ; в случае, если , то
Пунктирными линиями на графике выстроим асимптоты.
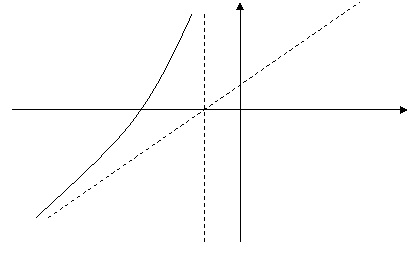У
-3 -1 О 1 х
-3
7.3. Схема полного изучения функции
1. Отыскать область определения функции.
2. Отыскать точки пересечения графика функции с осями координат (нули функции).
3. Изучить функцию на «чётность — нечётность». В случае, если , то функция именуется чётной и её график симметричен относительно оси Оу. В случае, если , то функция именуется нечётной и её график симметричен относительно начала координат. В случае, если функция не есть ни чётной ни нечётной, то её именуют функцией неспециализированного вида.
4. Проверка периодичности функции (в большинстве случаев для тригонометрических функций).
5. Отыскать асимптоты (вертикальные, наклонные)
6. Изучение посредством 1-й производной (критические точки, промежутки монотонности, экстремумы).
7. Изучение посредством 2-й производной (промежутки выпуклости, точки перегиба).
8. Построение графика.
Разглядим примеры.
1 Совершить полное изучение и выстроить график функции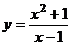 
.
1) Область определения: , т.е.
.
2). Нули функции: . в ноль обращаться не имеет возможности.
3). 
.
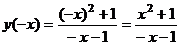следовательно функция неспециализированного вида.
4). Не периодична.
5). Асимптоты. Вертикальная асимптота вероятна в точке . Отыщем в данной точке односторонние пределы.
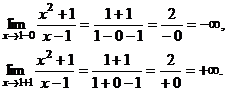
Следовательно, — вертикальная асимптота.
Отыщем наклонную асимптоту.
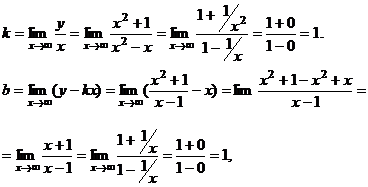
т.е. наклонная асимптота имеет уравнение
6). Изучение посредством 1-й производной.
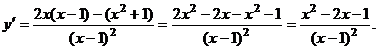
Критические точки: .
Определим точки экстремума и интервалы монотонности. Пост- роим числовую ось
+ — +
1
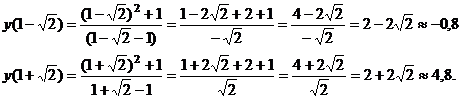
6. Изучение посредством 2-й производной
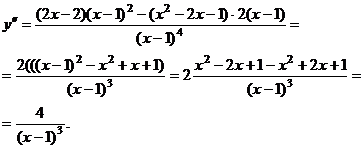
Выстроим числовую прямую
— 1 + х
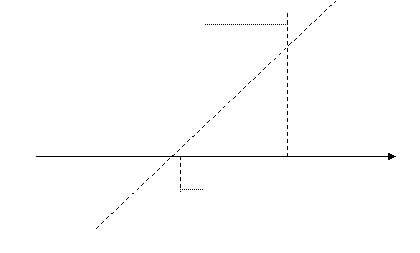
Выстроим график
Y
4,8
-1 -0,4 O 1 2,4 x
— 0,8
2. Совершить полное изучение и выстроить график функции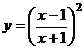 
.
1). Область определения данной функции: , либо .
2). Нули функции:
3). 
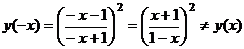и , т.е. функция неспециализированного вида.
4). Не периодична.
5). Вертикальная асимптота вероятна в точке . Отыщем односторонние пределы в данной точке:
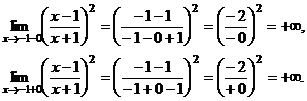
В точке график имеет вертикальную асимптоту.
Отыщем наклонную асимптоту в виде .
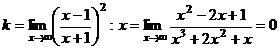, так как степень числителя меньше степени знаменателя.
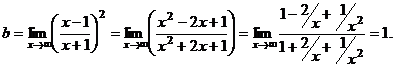
Так, график имеет горизонтальную асимптоту
6). Изучение посредством 1-й производной:
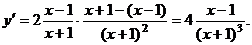
Критическая точка : при . Выстроим числовую прямую
+ -1 — 1 + х
7) Изучение посредством 2-й производной:
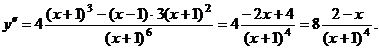
при . Выстроим числовую ось:
+ -1 + 2 _ х
8). Осталось выстроить график
 |
 |
||
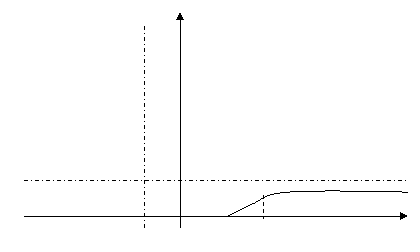
у
-1 О
1 2 х
Разглядим ещё один пример для случая, в то время, когда график функции имеет одностороннюю асимптоту
3. Совершить полное изучение и выстроить график функции .
1). Область определения данной функции — вся числовая прямая.
2) Нули функции:
3). и , т.е. функция неспециализированного вида.
4).. Не периодичная.
5). Вертикальных асимптот нет, поскольку нет точек разрыва.
При нахождении наклонных асимптот будет необходимо раздельно обнаружить пределы при и , из — за особенностей показательной функции.
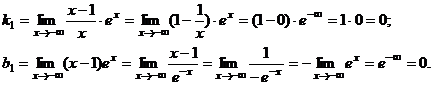(При вычислении второго предела мы применяли правило Лопиталя). Итак, при график имеет горизонтальную асимптоту .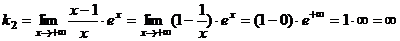 
Следовательно, при график асимптоты не имеет.
6).
при В случае, если при .
Следовательно, в точке функция имеет минимум
7). Отыщем вторую производную
.
при . В случае, если и график имеет выпуклость, направленную вверх. В случае, если и график имеет выпуклость, направленную вниз.
Выстроим график функции.
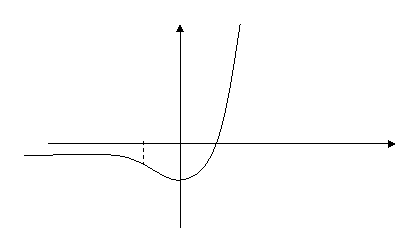
Y
-1 0 1 x
-1
Так возможно выстроить график любой функции.
Библиографический перечень.
Математика без Ху%!ни. Исследование функции, график. Первая, вторая производная, асимптоты.
Интересные записи:
- История литературы стран изучаемого языка.
- Итак вера от слышания, а слышание от слова божия. (послание к римлянам 10:17)
- I. тема№12: мышцы и фасции тазового пояса и свободной нижней конечности: строение, топография и функции. топография нижней конечности.
- Итоговый тест по учебной дисциплине «психология» для студентов 4 курса направления «теология»