КУРС ЛЕКЦИЙ ПО АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ и АЛГЕБРЕ
Учебно — Методическое пособие
для студентов инжинерно-технического
факультета ПГУ им. Т.Г. Шевченко
Издательство
Приднестровского
Университета
Тирасполь,2008
УДК
ББК
В-22
Составители:
Л.С. Николаева, ст. преп.
Л.В. Чуйко, канд. Пед. Наук, доц.
Критики:
Курс лекций по аналитической геометрии и алгебре.: Учебно – методическое пособие / Сост.:
Л.С. Николаева, Л.В. Чуйко. – Тирасполь, 2008. – 80 с.
УДК
ББК
В-26
Утверждено Научно-методическим советом ПГУ им. Т.Г. Шевченко
© Николаева Л.С.
Чуйко Л.В.,
составление, 2008
Оглавление.
Раздел: Линейная алгебра.
- Совокупности линейных уравнений и их ответ способом Гаусса. (4)
- Алгебра матриц. Операции над матрицами. Обратная матрица. Матричное уравнение вида AX=B, совокупность линейных уравнений как матричное уравнение(8)
- Определитель квадратной матрицы.(13)
- Матричный способ ответа совокупностей линейных уравнений.(16)
- Способ Крамера.(18)
- Понятие векторного пространства(19)
- независимость системы и Линейная зависимость векторов(20)
- размерность и Базис векторного пространства(22)
- Координатная строчок вектора относительно базиса(23)
- Связь между координатами вектора в различных базисах(24)
- Подпространство векторного пространства(25)
- Векторное пространство со скалярным умножением. Определение евклидова пространства(26)
- Протяженность вектора.Угол между векторами(26)
- Ортогональный базис евклидова пространства(27)
- Ортонормированный базис(28)
- Линейные отображения (операторы) векторных пространств(29)
- Матрица линейного оператора(31)
- Личные вектора и личные значения линейного оператора.(33)
Раздел: Аналитическая геометрия.
- Афинная совокупность координат на плоскости.(33)
- Полярная совокупность координат. Переход от полярной совокупности к декартовой и обратно.(36)
- Уравнение линии на плоскости.Уравнение прямой на плоскости.(37)
- Угол между прямыми на плоскости.(41)
- Расстояние от точки до прямой.(42)
- Кривые второго порядка: окружность(43), эллипс(44), преувеличение(46), парабола(48)
- Афинная совокупность координат в пространстве.(51)
- Векторное произведение двух векторов.(54)
- Смешанное произведение трёх векторов.(56)
- Разные методы задания плоскости. Неспециализированное уравнение плоскости.(58)
- Обоюдное размещение двух плоскостей в пространстве.(61)
- Разные методы задания прямой в пространстве.(62)
- плоскости и Взаимное расположение прямой.(65)
- Обоюдное размещение двух прямых.(66)
- Угол между плоскостями.(67)
- Угол между прямыми в пространстве.(68)
- Угол между плоскостью и прямой.(69)
- Расстояние от точки до плоскости.(70)
- Расстояние от точки до прямой.(71)
- Расстояние между двумя скрещивающимися прямыми.(72)
- Поверхности второго порядка:цилиндрические поверхности(73), поверхности вращения(74)
- Цилиндрическая и сферическая совокупности координат(78)
АЛГЕБРА.
Совокупности линейных уравнений и их ответ способом Гаусса.
- Линейное уравнение. Вид противоречивого линейного уравнения. Неспециализированный вид совокупности линейных уравнений (СЛУ). Множество ответов.
- Равносильные совокупности. Следствие совокупности.
- Элементарные преобразования совокупности линейных уравнений.
- Способ Гаусса ответа СЛУ. Распределение малоизвестных на главные и свободные.
В общем виде линейное уравнение (уравнение первой степени) имеет форму
a1x1+a2x2+…+anxn=b (1)
где ai,b R, . x1,x2,…,xn– малоизвестные переменные, ai — коэффициенты при малоизвестных, b – вольный член. Не исключается случай, в то время, когда уравнение имеет форму
0x1+0x2+…+0xn=b (2)
Ответом уравнения (1) именуется любой упорядоченный комплект чисел l1,l2,…,ln (либо вектор (l1,l2,…,ln)), таких что при подстановке их вместо соответствующих малоизвестных уравнение (1) обращается в верное равенство
a1l1+a2l2+…+anln=b
Разумеется, что при b=0 уравнение (2) имеет любой комплект значений малоизвестных, а при b?0 не удовлетворяет несколько комплект ответов. При b=0 уравнение (2) именуют тождественным, а при b?0 противоречивым.
Определение. Совокупность m уравнений с n малоизвестными в общем виде записывается следующим образом:
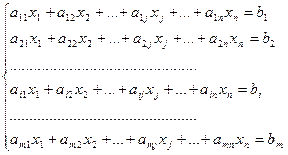(3),
где aij – коэффициенты, а bi – постоянные. Ответом совокупности именуется любой упорядоченный комплект чисел l1,l2,…,ln (либо вектор (l1,l2,…,ln)), таких, что при подстановке их в совокупность вместо соответствующих переменных они превращают каждое уравнение совокупности в тождество.
Вычеркнем из записи линейной совокупности уравнений знаки xi,+,= и отделим коэффициенты при малоизвестных от свободных участников вертикальной чертой, возьмём запись:
Ф такая таблица именуется расширенной матрицей совокупности, матрицей совокупности назовём таблицу следующего вида
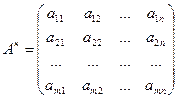
Определение. В случае, если совокупность имеет хотя бы одно ответ, то она именуется совместной. В случае, если совокупность не имеет ни одного решения, то она именуется несовместной.
Определение. Совокупность именуется определенной, если она имеет лишь одно ответ и неизвестной, в случае, если более одного.
Для любой совокупности вероятны лишь три случая:
- совокупность несовместна;
- совокупность имеет единственное ответ (совместно определённая);
- совокупность имеет очень много ответов (совместно неизвестная).
Промежуточный случай, в то время, когда ответов конечное число, притом больше чем одно, неосуществим.
Совокупность S1 именуется следствием совокупности S2, в случае, если всякое ответ совокупности S1 есть ответом совокупности S2 либо совокупность S1 несовместна.
Две линейные совокупности именуются равносильными (эквивалентными), в случае, если любая из них есть следствием второй, другими словами совокупности равносильны, в случае, если множества их ответов совпадают.
Элементарными преобразованиями (расширенной) матрицы именуют следующие действия над её строчками:
- перестановка i-той и j-той строчков. Этому преобразованию соответствует перестановка i-того и j-того уравнения. Обозначим это преобразование .
- прибавление к каждому элементу i-той строки, стоящего в том же столбце элемента j- той строки. Этому преобразованию соответствует сложение i-того и j-того уравнения. Обозначим это преобразование .
- умножение каждого уравнения i-той строки на некое число . Этому преобразованию соответствует умножение i-того уравнения на число . Обозначим это преобразование .
В случае, если J-это преобразование матрицы А, то J=J(A).
Теорема.Элементарные преобразования расширенной матрицы сохраняют эквивалентность соответствующих совокупностей.
Подтверждение. Пускай заданы две совокупности линейных уравнений: совокупность S1 в виде(3) и совокупность S2 в виде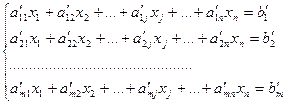 
( ) с множествами ответов М1 и М2 соответственно. Причём как мы знаем, что расширенная матрица совокупности S2 взята элементарными преобразованиями из расширенной матрицы совокупности S1. Докажем, что М1=М2, другими словами М1 М2 и М2 М1. Докажем вначале
М1 М2.
Допустим ответ (l1,l2,…,ln) М1, докажем что (l1,l2,…,ln) М2. Разглядим следующие случаи:
Пускай J=Iij, это указывает, что совокупность S2 взята из совокупности S1 перестановкой i-того и j-того уравнения. Ясно, что при подстановке чисел l1,l2,…,ln в совокупность S2 мы возьмём m верных равенств, но записанных в другом порядке. Следовательно (l1,l2,…,ln) М2, другими словами М1 М2.
Пускай J=IIij, это указывает, что уравнения в совокупности S2, не считая j-того, остались неизменными. j-тое уравнение имеет форму
Потому, что (l1,l2,…,ln) — ответ S1, подстановка чисел lk в её i-тое и j-тое уравнения даёт следующих два верных равенства:
Сложим их почленно и приведём подобные при участниках lk. Возьмём верное равенство
Легко видеть, что это и имеется итог подстановки чисел lk в j-тое уравнение совокупности S2.
Пускай J= , это указывает, что уравнения в совокупности S2, не считая j-того, остались неизменными, а j-тое уравнение почленно умножается на число и имеет форму
Потому, что (l1,l2,…,ln) М1, правильно равенство
соответственно, и равенство , которое и имеется итог подстановки чисел lk в i-тое уравнение совокупности S2. Итак, М1 М2.
Перед тем как обосновывать обратное включение, увидим, что матрица совокупности S1 возможно взята элементарными преобразованиями из матрицы совокупности S2. (В действительности, в случае, если две строки переставлены, их возможно опять переставить, в случае, если к i-той прибавлена j-тая, то i-тую возможно умножить на -1, сложить с j-той и позже опять умножить на -1, в случае, если строчок умножена на , то её возможно умножить на . Вот где мы используем то, что .) Тогда, по доказанному, М2 М1.
Способ Гаусса.
(Карл Фридрих Гаусс (1777-1855) германский математик).
Универсальным способом ответа линейных совокупностей есть способ последовательного исключения малоизвестных ( способ Гаусса).
Разглядим совокупность (3). Если она содержит уравнение вида (2) и b , то множество ответов пусто. Процесс ответа на этом закончен. В случае, если в уравнении (2) и b=0, то его возможно удалить из совокупности, не изменяя множества ответов. Исходя из этого можно считать, что в каждом уравнении исходной совокупности хотя бы один из коэффициентов при малоизвестных отличен от нуля. Пускай а11 ( в другом случае поменяем местами уравнения либо перенумеруем малоизвестные). Исключим сейчас x1 из всех уравнений, начиная со второго. Для этого ко второму уравнению прибавим первое, умноженное на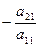 
, после этого к третьему уравнению прибавим первое, умноженное на 
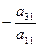, и т.д. к последнему уравнению прибавим первое, умноженное на 
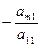. В следствии серии элементарных преобразований возьмём совокупность:
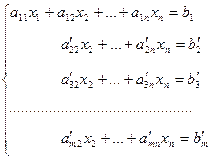(4)
равносильную исходной. Удалим из совокупности (4) нулевые уравнения (поэтому, в ходе ответа совокупности число уравнений может уменьшиться). В случае, если хотя бы одно из уравнений совокупности (4) есть противоречивым, то эта совокупность и, следовательно, исходная совокупность несовместны.
Потом предположим, что а22 , и продолжим процесс исключения малоизвестных. Потому, что число таких шагов не превышает n (числа малоизвестных), по окончании конечного числа преобразований возьмём совокупность вида:
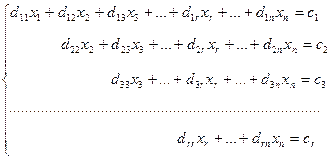(5)
(где диагональные коэффициенты d11,d22,d33,…,drr ,r ,хороши от нуля), равносильную исходной совокупности (3).
В случае, если r=n ( в этом случае говорят, что совокупность (5) имеет треугольный вид), то из последнего уравнения находим значения малоизвестной xn= . Подставив значение xn в предпоследнее уравнение, возьмём значение малоизвестной xn-1 и т.д., другими словами идя снизу в верх, определим значения всех малоизвестных.
Итак, при r=nрешение совокупности (5) ( соответственно, и (3) ) единственно.
В случае, если r
(l1, l2,…, lr, lr+1, lr+2,…, ln) исходной совокупности уравнений. Любое ответ совокупности (3) возможно взять так.
Совокупность, в которой главные малоизвестные выражены через свободные, возможно разглядывать как общее решениеисходной совокупности, т.е. как характеристическое свойство множества её ответов.
Так, при r
Пример. Решить совокупность линейных уравнений способом Гаусса.
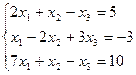
Составим расширенную матрицу совокупности.
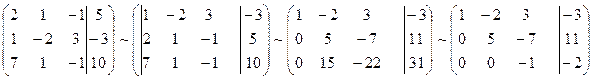
Так, исходная совокупность возможно представлена в виде:
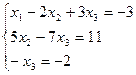, откуда приобретаем: x3 = 2; x2 = 5; x1 = 1.
Для независимого ответа:
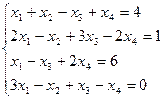Ответ: {1, 2, 3, 4}.
Алгебра матриц. Операции над матрицами. Обратная матрица. Матричное уравнение вида AX=B, совокупность линейных уравнений как матричное уравнение(операции сложения, умножения, транспонирование матриц, умножение матрицы на число, вычисление обратной матрицы посредством элементарных преобразований, теоремы о ранге произведения матриц).
Пускай P – некое поле (поле скаляров). Матрицы, составленные из элементов этого поля, будем именовать матрицами порядка m´n, где m и n натуральные числа показывающие число столбцов и строк (это таблица чисел, расположенных в определенном порядке). Место каждого элемента конкретно определяется номером столбца и строки, на пересечении которых он находится. Элементы матрицы обозначаются aij, где i- номер строчка, а j- номер столбца.
Обозначать матрицу будем так:
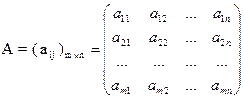
Матрица может состоять как из одной строки, так и из одного столбца. По большому счету говоря, матрица может состоять кроме того из одного элемента.
В случае, если число столбцов матрицы равно строчков (m=n), то матрица именуется квадратной порядка n.
Обозначим i-тую строчок матрицы Ai=(ai1,ai2,…,ain), а j-тый столбец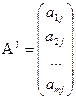 
.
Две матрицы порядка А=(aij)m n и B=(bij)m n именуются равными, в случае, если соответствующие элементы равны, т.е. A=B aij= bij, .
Матрица именуется нулевой, в случае, если все её элементы равны нулю.
Матрица вида:
,
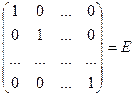именуется единичной матрицей.
Определение. В случае, если aij = aji , то матрица именуется симметрической.
Пример.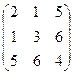 
— симметрическая матрица
Определение.Квадратная матрица вида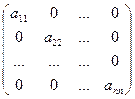 
именуется диагональнойматрицей.
вычитание и Сложение матриц сводится к соответствующим операциям над их элементами. Самым главным свойством этих операций есть то, что они выяснены лишь для матриц однообразного размера. Так, допустимо выяснить вычитания матриц и операции сложения:
Определение. Суммой (разностью) матриц есть матрица, элементами которой являются соответственно сумма (разность) элементов исходных матриц.
cij = aij ± bij
С = А + В = В + А.
Операция умножения (деления) матрицы любого размера на произвольное число сводится к умножению (делению) каждого элемента матрицы на это число.
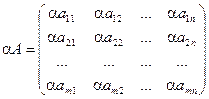
a (А+В) =aА ± aВ
А(a±b) = aА ± bА
Пример. Даны матрицы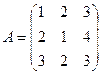 
; 
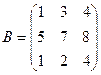, отыскать 2А + В.
, 
.
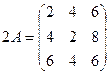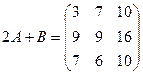Операция умножения матриц.
Разглядим матрицы А порядка m´n и В порядка n´k .
Произведением строчка Ai на столбец Br определим следующим образом:
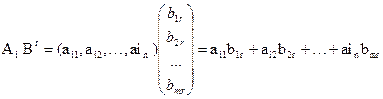
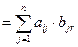
Произведением матрицы А на матрицу В назовём матрицу F порядка m´k, такую, что fij=AiBJ
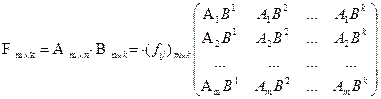
Из приведенного определения видно, что операция умножения матриц выяснена лишь для матриц, число столбцов первой из которых равно строчков второй.
Яркий анализ определения операции умножения матриц говорит о том, что любой столбец произведения матриц А и В линейно выражается через совокупность столбцов матрицы А, а любая строчок этого произведения линейно выражается через совокупность строчков матрицы В. Либо подробнее: j- тый столбец матрицы АВ имеется линейная комбинация всех столбцов матрицы А, а коэффициенты данной комбинации – элементы j- того столбца матрицы В, i- тая строчок матрицы АВ имеется линейная всех строчков матрицы В, а коэффициенты данной линейной комбинации – элементы i- той строки матрицыА. Эти утверждения лежат в базе доказательства первой теоремы о ранге произведения матриц: ранг произведения матриц не превосходит ранга каждого из сомножителей :
r(AB) r(A), r(AB) r(B).
Пример. Отыскать произведение матриц ,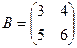 
? 
= = .
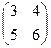Произведение ВА не существует, поскольку число столбцов матрицы В (=2) не равно строчков матрицы А (=1).
Пример. Отыскать произведение матриц А = и В = .
АВ = ? =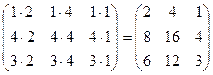 
.
ВА = ? = (2?1 + 4?4 + 1?3 )= (2 + 16 + 3) = (21).
Свойства операций над матриц.
1) Сумма матриц коммутативна и дистрибутивна
А+В=В+А
(А+В)+С=А+(В+С).
2) Умножение матриц не коммутативно, т.е. АВ ¹ ВА кроме того в случае, если выяснены оба произведения. Но, в случае, если для каких – или матриц соотношение АВ=ВА выполняется, то такие матрицы именуются перестановочными.
Самым характерным примером может служить единичная матрица, которая есть перестановочной с каждый матрицей того же размера.
Перестановочными смогут быть лишь квадратные матрицы одного и того же порядка.
А?Е = Е?А = А
Разумеется, что для любых матриц выполняются следующее свойство:
A?O = O; O?A = O,
где О – нулеваяматрица.
3) Операция перемножения матриц ассоциативна, т.е. в случае, если выяснены АВ и произведения (АВ)С, то выяснены ВС и А(ВС), и выполняется равенство:
(АВ)С=А(ВС).
4) Операция умножения матриц дистрибутивна по отношению к сложению, т.е. в случае, если имеют суть выражения А(В+С) и (А+В)С, то соответственно:
А(В + С) = АВ + АС
(А + В)С = АС + ВС.
5) В случае, если произведение АВ выяснено, то для любого числа a правильно соотношение:
a(AB) = (aA)B = A(aB).
6) В случае, если выяснено произведение АВ , то выяснено произведение ВТАТ и выполняется равенство:
(АВ)Т = ВТАТ, где
индексом Т обозначается транспонированная матрица.
6) Увидим кроме этого, что для любых квадратных матриц det (AB) = detA?detB.
Понятие det (определитель, детерминант) будет рассмотрено ниже..
Определение. Матрицу В именуют транспонированнойматрицей А, а переход от А к В транспонированием, в случае, если элементы каждой строки матрицы А записать в том же порядке в столбцы матрицы В.
А =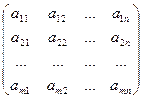 
; В = АТ= 
;
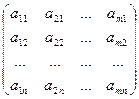иначе говоря bji = aij.
В качестве следствия из прошлого свойства (5) возможно записать, что:
(ABC)T = CTBTAT,
при условии, что выяснено произведение матриц АВС.
Пример. Даны матрицы А =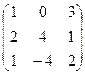 
, В = , С = 
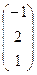и число a = 2. Отыскать АТВ+aС.
AT =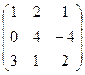 
; ATB = ? = 
= 
;
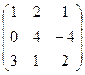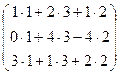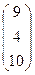aC =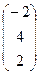 
; АТВ+aС = + = 
.
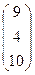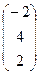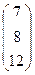Матричный способ ответа совокупностей линейных уравнений.
Матричный способ применим к ответу совокупностей уравнений, где число уравнений равно малоизвестных.
Способ удобен для ответа совокупностей низкого порядка.
Способ основан на применении особенностей умножения матриц.
Пускай дана совокупность уравнений:
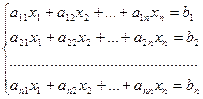
Составим матрицы: A =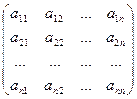 
; B = 
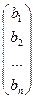; X =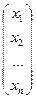 
,
где А- главная матрица совокупности, X- одностолбцовая матрица, составленная из малоизвестных данной совокупности, В — одностолбцовая матрица из её свободных участников.
Совокупность уравнений возможно записать в матричном виде:
A?X = B.
Совокупность линейных уравнений представляет собой частный случай матричных уравнений вида A?X = B. Уравнение вида YA=B сводятся к этому же типу матричных уравнений, потому, что (YA)Т=BТ и в следствии AТ?YT = BT.
Cогласно определению умножения матриц, A?X = B не имеет ответов, в случае, если матрицы А,В имеют разное число строчков. Исходя из этого имеет суть разглядывать матричные уравнение, в которых строчков у матриц А и В одно да и то же.
В случае, если В – k столбцовая матрица, то матричное уравнение A?X = B распадается на совокупность k матричных уравнений: A?X1 = B1, A?X2 = B2,…, A?Xk = Bk.
Каждое из этих матричных уравнений есть совокупностью линейных уравнений, причём все они имеют матрицу А собственной главной матрицей, и их ответами будут столбцы малоизвестной матрицы X. В большинстве случаев, все эти линейные совокупности решаются в один момент, в виде пакета.
Критерий разрешимости матричных уравнений:
Матричное уравнение A?X = B имеет ответ тогда и лишь тогда, в то время, когда ранг матрицы А равен рангу матрицы ( ), т.е. матрицы взятой из матрицы А присоединением к ней матрицы В.
Квадратную матрицу, ранг которой равен её порядку, именуют невырожденной. В случае, если ранг квадратной матрицы меньше её порядка, матрица вырождена. Увидим, что в случае, если в матричном уравнении A?X = B матрица А невырожденная, то это уравнение имеет единственное ответ, поскольку любая из этих совокупностей линейных уравнений, на каковые оно распадается, будет совместно определенной.
Как мы знаем, что квадратная матрица n порядка вида:
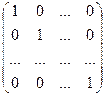= E,
именуется единичной матрицей. Разумеется, что в случае, если А – квадратная матрица n порядка, то A?Еn = En?A =A.
В случае, если A?С = Е, то матрицу С именуется правой обратной для матрицы А, а матрицу А – левой обратной для матрицы С.
Видно, что матрица С есть ответом матричного уравнения A?X =Е, причем, в случае, если А – невырожденная матрица, это решение единственное. Следовательно, любая невырожденная матрица имеет единственную правую обратную матрицу. Возможно доказать( применяя первую теорему о ранге произведения и ассоциативность умножения), что правая обратная матрица есть и левой обратной. Итак,любая невырожденная матрица имеет единственную двустороннюю обратную матрицу, которую обозначают А-1:
A-1A=AA-1=E.
Одним из способов нахождения матрицы, обратной для матрицы А, есть ответ матричного уравнения A?X =Е.
В соответствии с первой теореме о ранге произведения матриц, r(AB) r(B).
В случае, если матрица невырожденная, то матрицу В возможно записать в виде В=А-1(АВ), и тогда (по той же теореме) r(AB) r(B). Тем самым доказана вторая теорема о ранге произведения матриц: в случае, если матрица А невырожденная, то r(AB)=r(B).