Группировка — это распределение единиц совокупности по группам в соответствии с группировочным показателем. Назначение группировки пребывает в том, что данный способ снабжает обобщение данных, представление их в компактном, обозримом виде. На базе группировки рассчитываются сводные показатели по группам, появляется возможность их сравнения, изучения связей между показателями.
Различия в целевом назначении группировки выражаются в существующей в отечественной статистике классификации группировок: типологические, структурные, аналитические.
При осуществлении любой группировки решается вопрос об определении числа выделяемых групп. При группировке по количественному показателю вопрос о числе групп решается на базе выделения однородных, родных по значению показателя единиц совокупности. Нужно, дабы любая несколько характеризовала значительные типы явления. Число единиц в выделенных группах должно быть достаточным, дабы характеристики, вычисленные для отдельных групп были статистически устойчивыми. Количество выделяемых групп зависит от вариации показателя, числа наблюдений, и от количества отдельных вероятных значений показателя, т.е. от числа вариант показателя. При маленьком числе вариант показателя, положенного в базу группировки, любая варианта воображает отдельную группу.
В случае, если число вариант громадно, то значения группировочного показателя для отдельных групп указываются в промежутках «от – до». Для этого всю область трансформации показателя разбивают на пара промежутков и вычисляют, сколько элементов попадает в отдельный промежуток. Промежутки смогут быть равными и неравными, открытыми и закрытыми. Группировку с неравными промежутками нужно применять, в случае, если размах вариации показателя в совокупности велик, неравные промежутки используются как прогрессивно возрастающие либо убывающие. В этом случае границы каждого промежутка устанавливаются исследователем. Но нужно учесть, что наличие равных промежутков технически существенно облегчает вычисление разных статистических черт.
Равные промежутки используются в случаях, в то время, когда изменение показателя в совокупности происходит равномерно. Расчет величины промежутка при равных промежутках производится по формуле:
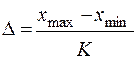 ,
,
где D — величина отдельного промежутка,
xmax — большое значение показателя в исследуемой совокупности,
xmin — минимальное значение показателя в исследуемой совокупности.
K — число групп,
После этого определяются границы каждого промежутка:
для первого промежутка: от xmin до xmin +D;
для второго промежутка: от xmin + D до xmin + 2D ;
………………………………………………………………
для промежутка: K от xmin + KD до xmax.
Типологическая группировка помогает для обнаружения типов элементов явлений.
Структурная группировка помогает для изучения совокупности по одному показателю.
По окончании того, как в следствии сводки статистику сгруппированы, они, в большинстве случаев, представляются в виде таблицы. Макет таблицы для представления результатов структурной группировки может выглядеть следующим образом:
Наименование таблицы
| Наименование группировочного показателя, (единицы измерения) | Количество единиц совокупности в отдельной группе | В процентах к итогу |
| … | … | … |
| … | … | … |
| … | … | … |
| Итого | Неспециализированное число элементов совокупности |
Тут в первой графе указываются варианты (промежутки) значений показателя для отдельных групп по возрастанию либо убыванию.
Аналитические группировки помогают для обнаружения аналитической зависимости между группировочными показателями. При построении аналитических группировок принципиально важно верно выяснить показатель-признак и результат-фактор.
Показатель, влияние которого на другие показатели исследуется, именуется показателем-фактором. Показатель, испытывающий влияние факторного, именуется показателем — результатом. Дабы установить связь между показателями аналитическая группировка осуществляется по показателю-фактору. После этого по каждой группе отбираются соответствующие значения показателя-результата и рассчитывается его среднее значение. Сопоставляя изменение средних значений показателя-результата от группы к группе с трансформациями показателя-фактора возможно сделать вывод о наличии либо отсутствии связи, и о ее направлении. Различие групповых средних разрешает утверждать, что показатели взаимозависимы. В случае, если изменение величины показателя-фактора в определенном направлении приводит к изменению величины показателя-результата в том же направлении, то сообщение прямая, в другом случае — сообщение обратная.
Макет таблицы для представления результатов аналитической группировки может выглядеть следующим образом:
Наименование таблицы
| Наименование показателя-фактора (единица измерения) | Количество элементов совокупности в отдельной группе | Среднее значение показателя-результата (единица измерения) |
| … | … | … |
| … | … | … |
| … | … | … |
| Итого | Неспециализированное число элементов совокупности | — |
Тут в первой графе указываются варианты (промежутки) значений показателя-фактора для отдельных групп по возрастанию либо убыванию.
Проследить зависимость между факторами возможно кроме этого на базе комбинационной группировки. Комбинационная группировка осуществляется в один момент по двум и более показателям, забранным в сочетании.
Макет комбинационной таблицы выглядит следующим образом:
Наименование таблицы
| Группировка по показателю- | Группировка по показателю-результату | Всего | ||||
| фактору | ||||||
| n11 | n12 | … | n1M | Sn1j | ||
| n21 | n22 | … | n2M | Sn2j | ||
| … | … | … | … | … | ||
| nK1 | nK2 | … | NKM | SnMj | ||
| Всего | Sni1 | Sni2 | … | SniK | Snij |
Тут nij — частота совместного появления значения i показателя-фактора (i = 1, 2,..,M) и значения j показателя результата (j = 1,2,…,K).
В случае, если громаднейшие частоты каждой каждого столбца и строки находятся на протяжении диагонали таблицы, идущей от левого верхнего угла таблицы к правому нижнему, то возможно сделать вывод, что связь между показателями есть прямой и близкой к линейной.
В случае, если громаднейшие частоты находятся на протяжении диагонали от правого верхнего угла к нижнему левому, то сообщение — обратная и близкая к линейной.
В случае, если частоты во всех клетках таблицы приблизительно однообразны, то связи между показателями нет.
Контрольное задание №1
На базе данных, приведенных в Приложении 1 и соответствующих Вашему варианту (таблица 1), выполнить:
1. Структурную равноинтервальную группировку по обоим показателям. В случае, если вариация группировочного показателя велика и его значение для отдельных групп нужно представить в виде промежутков, то при построении группировки по показателю № 1 принять число групп равным 7, а по показателю № 2 — 8. Результаты представить в таблице, сделать выводы.
2. Аналитическую группировку, для этого выяснить показатель-признак и результат-фактор, обосновав их выбор. При построении аналитической группировки применять равнонаполненную группировку по показателю-фактору (в каждой группе примерно однообразное количество наблюдений). Результаты группировки представить в таблице. Сделать выводы о направлении и наличии связи между показателями.
3. Комбинационную группировку по показателю-признаку и фактору-результату. Сделать выводы.
Таблица данных для создания статистической совокупности
Таблица 1
| Последние две цифры № зачетной книжки | Номер начального наблюдения | Номер конечного наблюдения | Номера показателей из приложения 1 | Последние две цифры № зачетной книжки | Номер начального наблюдения | Номер конечного наблюдения | Номера показателей из приложения 1 |
| 1,2 | 1,3 | ||||||
| 3,4 | 4,5 | ||||||
| 1,3 | 1,4 | ||||||
| 4,5 | 2,5 | ||||||
| 1,4 | 1,5 | ||||||
| 2,5 | 2,3 | ||||||
| 1,5 | 1,2 | ||||||
| 2,3 | 3,4 | ||||||
| 1,2 | 1,3 | ||||||
| 3,4 | 4,5 | ||||||
| 1,3 | 1,4 | ||||||
| 4,5 | 2,5 | ||||||
| 1,4 | 1,5 | ||||||
| 2,5 | 2,3 | ||||||
| 1,5 | 1,2 |
Окончание таблицы 1
| 2,3 | 3,4 | ||||||
| 1,2 | 1,3 | ||||||
| 3,4 | 4,5 | ||||||
| 1,3 | 1,4 | ||||||
| 4,5 | 2,5 | ||||||
| 1,4 | 1,5 | ||||||
| 2,5 | 2,3 | ||||||
| 1,5 | 1,2 | ||||||
| 2,3 | 3,4 | ||||||
| 1,2 | 1,3 | ||||||
| 3,4 | 4,5 | ||||||
| 1,3 | 1,4 | ||||||
| 4,5 | 2,5 | ||||||
| 1,4 | 1,5 | ||||||
| 2,5 | 2,3 | ||||||
| 1,5 | 1,2 | ||||||
| 2,3 | 3,4 | ||||||
| 1,2 | 1,3 | ||||||
| 3,4 | 4,5 | ||||||
| 1,3 | 1,4 | ||||||
| 4,5 | 2,5 | ||||||
| 1,4 | 1,5 | ||||||
| 2,5 | 2,3 | ||||||
| 1,5 | 1,2 | ||||||
| 2,3 | 3,4 | ||||||
| 1,2 | 1,3 | ||||||
| 3,4 | 4,5 | ||||||
| 1,3 | 1,4 | ||||||
| 4,5 | 2,5 | ||||||
| 1,4 | 1,5 | ||||||
| 2,5 | 2,3 | ||||||
| 1,5 | 1,2 | ||||||
| 2,3 | 3,4 | ||||||
| 1,2 | 1,3 | ||||||
| 3,4 | 4,5 |
Методические указания к исполнению задания №2
Обощающие характеристики совокупностей
Анализ статистических совокупностей включает в себя: построение последовательностей распределения; графическое представление распределения; определение черт центра распределения, показателей вариации.
Последовательностями распределения именуют числовые последовательности, характеризующие структуру совокупности по некоему показателю. Последовательность распределения возможно взят в следствии структурной группировки. Последовательность распределения, образованный по количественному показателю (он именуется вариационным рядом), возможно дискретным, в случае, если значения показателя выражены целыми числами и любая варианта представлена в вариационном последовательности отдельной группой, либо интервальным (постоянным), в случае, если значения показателя выражены вещественными числами либо число вариант показателя велико.
Последовательность распределения складывается из следующих элементов:
xi — варианта- отдельное, вероятное значение показателя i=1,2,…,K, где K — число значений показателя;
Ni — частоты — численность отдельных групп соответствующих значений показателей;
N — количество совокупности — неспециализированное число элементов совокупности;
qi — частость — часть отдельных групп во всей совокупности;
Di — величина промежутка;
— полная плотность распределения;
— относительная плотность распределения.
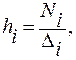
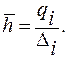
Полученный вариационный последовательность оформляется в виде таблицы, где в первой графе указываются варианты (промежутки) значений показателя, а в следующих графах частота, частость, либо в случае, если нужно безотносительная либо относительная плотность распределения.
Последовательность распределения по частоте (частости) в целом характеризует структуру совокупности по этому показателю. Но для описания распределения совокупность смогут употребляться и кумулятивные последовательности, т.е. последовательности накопленных частот (либо частостей), каковые время от времени имеют кроме того кое-какие преимущества.
Накопленная частота (частость) данного значения показателя — это число (часть) элементов совокупности, личные значения показателя которых не превышают данного.
Обозначим: F(x) — накопленная частота для данного значения x;
G(x) — накопленная частость для данного значения x.
Эти характеристики владеют следующими особенностями:
0 ? F(x) ? N; 0 ? G(x) ? 1
Разглядим промежутки [xi -xi+1], i=1,2,…,K:
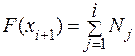 .
.
Первым этапом изучения вариационного последовательности есть его графическое изображение. Методы построения графиков для различных видов последовательностей распределения разны.
Изображением дискретного последовательности распределения есть полигон. В совокупности координат по оси абсцисс откладываются варианты (xi), по оси ординат — частоты (частости), после этого отмечают точки с координатами (xi;Ni), каковые последовательно соединяются отрезками прямой.
Интервальный последовательность распределения изображается графически в виде гистограммы. При её построении на оси абсцисс откладывают промежутки последовательности. Над осью абсцисс строятся прямоугольники, основанием которых есть промежуток, а высота — соответствующая этому промежутку полная плотность распределения (либо частота, частость — в случае, если последовательность равноинтервальный).
Изображением последовательности накопленных частот помогает кумулята. Накопленные частоты наносятся в совокупности координат в виде ординат для границ промежутков; соединяя нанесенные точки отрезками прямых, приобретаем кумуляту.
Вторым этапом изучения вариационного последовательности есть определение черт центра распределения. Черта центра распределения представляет собой такую величину,
которая в некоем отношении характерна для данного распределения и есть его центральной величиной.
К чертям центра распределения относятся: средняя арифметическая, медиана, мода.
Для сгруппированных данных, представленных в вариационном последовательности средняя арифметическая (`x) определяется как:
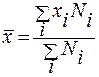 ,
,
т.е. в качестве веса при сглаживании берётся частота Ni, соответствующая групповым значениям xi. В случае, если последовательность дискретный, то каждое значение показателя представлено. В случае, если же последовательность интервальный, то его необходимо перевоплотить в условно дискретный: в качестве группового значения xi для каждого промежутка вычисляется его середина.
Медиана(Me[x]) — это такое значение показателя, которое дробит количество совокупности пополам в том смысле, что число элементов совокупности с личными значениями показателя, меньшими медианы, равна числу элементов совокупности с личными значениями больше медианы.
Численное значение медианы возможно выяснить по последовательности накопленных частот. Накопленная частота для Me[x] равна половине количества совокупности ( F(Me[x]) = N/2 ); имея последовательность накопленных частот, возможно вычислить, при каком значении показателя накопленная частота равна половине количества совокупности. Для интервального последовательности в этом случае определяется лишь промежуток в котором будет пребывать Me[x], само значение приближённо возможно выяснить как:
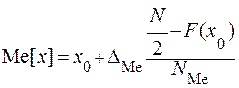 ,
,
где x0 — начало промежутка, содержащего медиану;
DMe — величина промежутка, содержащего медиану;
F(x0) — накопленная частота на начало промежутка, содержащего медиану;
N — количество совокупности;
NMe — частота того промежутка, в котором расположена медиана.
Квартили (Q1, Q2, Q3) – значения показателя, дробящие упорядоченную по значению показателя совокупность на 4 равные части. 1-ая квартиль (Q1) определяет такое значение показателя, что ¼ единиц совокупности имеют значения показателя меньше, чем Q1, а ¾ — значения больше чем Q1. 2-ая квартиль (Q2) равна медиане. 3-я квартиль (Q3) определяет такое значение показателя, что ¾ единиц совокупности имеют значения показателя меньше, чем Q3, а ¼ — больше чем Q3. Значения квартилей для сгруппированных данных определяются по накопленным частотам. Наряду с этим для 1-ой квартили накопленная частота сравнивается с величиной N·1/4; для 3-ей квартили – с величиной N·3/4. Значение квартили для интервального последовательности распределения возможно уточнено по формуле:
Qi=x0+DQi (i*N/4 – F(x0))/NQi.
x0- нижняя граница промежутка, в котором находится i-ая квартиль;
DQi — величина промежутка, содержащего i-ую квартиль;
F(x0) — сумма накопленных частот промежутков, предшествующих промежутку, в котором находится i-ая квартиль;
NQi — частота промежутка, в котором находится i-ая квартиль.
Децили (D1, D2, D3, D4, D5, D6, D7, D8, D9) – значения показателя, дробящие упорядоченную по значению показателя совокупность на 10 равных частей.
Мода (Mo[x]) — чаще всего видящееся значение показателя в совокупности.
Для дискретного последовательности — это то значение, которому соответствует громаднейшая частота распределения. Для интервального последовательности в начале определяется промежуток, содержащий моду, — тот, которому соответствует громаднейшая плотность распределения. После этого приближённо определяется численное значение моды.
В случае, если последовательность равноинтервальный, то употребляется формула:
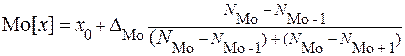 ,
,
где x0 — начало промежутка, содержащего моду,
DMo — величина промежутка, содержащего моду,
NMo — частота того промежутка, в котором расположена мода,
NMo-1 — частота промежутка, предшествующего модальному,
NMo+1 — частота промежутка, следующего за модальным.
Средняя величина характеризует лишь уровень, закономерный для данной совокупности. Во многих случаях одно да и то же численное значение средней может характеризовать совсем разные совокупности. Исходя из этого чтобы делать выводы о типичности средней для данной совокупности, её направляться дополнить показателями, характеризующими вариацию (колеблемость) показателя. Самый распространёнными из них являются дисперсия, среднее квадратичное отклонение, коэффициент вариации.
Дисперсия ( ) — это среднее из квадратов отклонений от средней величины, для вариационного последовательности она определяется по формуле:
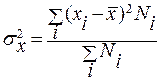 ,
,
В случае, если последовательность интервальный, то в качестве варианты (xi), кроме этого как при расчете средней, берётся середина промежутка.
При применении калькулятора, и для дискретных последовательностей распределения более эргономичной возможно вторая формула вычисления дисперсии:
где 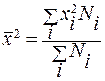
Самый обширно в статистике используется таковой показатель вариации, как среднее квадратичное отклонение ( ), что представляет собой квадратный корень из дисперсии.
Относительным показателем колеблемости показателя в данной совокупности, есть коэффициент вариации (V):
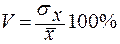
Коэффициент вариации разрешает сравнивать вариации разных показателей, и одноименных показателей в различных совокупностях.
Контрольное задание №2
1. На базе равноинтервальной структурной группировки (для любого показателя) выстроить вариационный частотный и кумулятивный последовательности распределения, оформить в таблице, изобразить графически.
2. Проанализировать вариационный последовательность распределения, вычислив:
- среднее арифметическое значение показателя;
- моду и медиану, квартили и децили (первую и девятую) распределения;
- среднее квадратичное отклонение;
- дисперсию;
- коэффициент вариации.
3. Сделать выводы.
Методические указания к исполнению задания №3
Индексы
В статистике под индексами понимаются относительные размеры, характеризующие результаты сравнения двух уровней одноименных объектов. Но это не каждые показатели сравнения, а особые, выстроенные при особенных условиях обобщения.
Любой индекс включает два вида данных: эти текущего (либо отчетного) уровня, каковые принято обозначать «1», и базового уровня, служащего базой сравнения, обозначаемые «0».
В зависимости от степени охвата подвергнутых обобщению единиц изучаемой совокупности индексы подразделяются на личные(частные) и агрегатные (неспециализированные).
Личные индексы характеризуют изменение отдельных единиц статистической совокупности (к примеру, изменение цен на отдельные виды услуг и работ и т.д.):
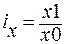
где x1 — текущий уровень индексируемой величины;
x0 — базовый уровень индексируемой величины.
Агрегатные индексы высказывают сводные обобщающие результаты совместного трансформации всех единиц, образующих статистическую совокупность (к примеру, изменение цен на все виды делаемых услуг и работ и т.д.):
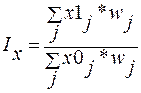 , где
, где
— коэффициент соизмерения;
— текущий уровень индексируемой величины;
— базовый уровень индексируемой величины.
Так как совокупность состоит в большинстве случаев из элементов, конкретно не поддающихся суммированию, то агрегатный индекс включает комплект значений индексируемой величины {xj} и соответствующих им коэффициентов соизмерения (весов) {wj}.
Ответственной изюминкой неспециализированных индексов есть то, что они владеют синтетическими и аналитическими особенностями. Синтетические особенности индексов пребывают в том, что при помощи индексного способа производится соединение в целое разнородных единиц статистической совокупности. Аналитические особенности определяются тем, что посредством индексного способа возможно оценить действие факторов на трансформацию изучаемого показателя.
Различают индексы количественных и качественных показателей. К индексам количественных (объемных) показателей относятся индексы физического количества продукции, услуг и работ, грузооборота, товарооборота и т.д. — показателей, каковые характеризуются безотносительными размерами. К индексам качественных показателей относятся индексы стоимостей, выработки, себестоимости единицы продукции, заработной платы и др., — показателей, уровень которых дается в форме средних (относительных) размеров.
Совокупность этих индексов возможно разглядеть на примере таких показателей, как цена, физический объем работ либо одолжений и цена работ либо одолжений.
Обозначим цену отдельного вида работ либо одолжений (качественный показатель) p, а физический количество, т.е. объем работ либо одолжений отдельного вида в натуральном выражении (количественный показатель) q.
Тогда личные индексы этих показателей имеют вид:
* физического количества работ либо одолжений ,
* цены ,
* стоимости .
При определении неспециализированного индекса стоимостей Ip существует два подхода: