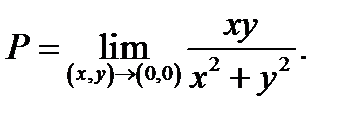Определение 2.Говорят, что на множестве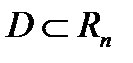 
задана функция 
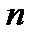переменных 
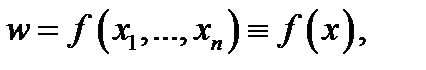отображающая множество 
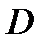в множество 
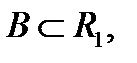в случае, если каждому 
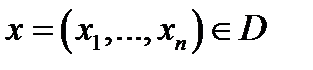поставлено в соответствие единственное число 
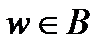по закону 
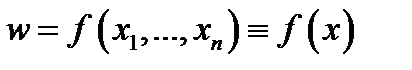. Наряду с этим множество 
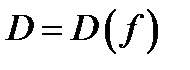именуется областью определения функции 
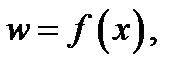а множество 
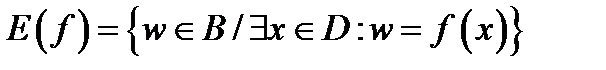именуется областью значений функции 
.
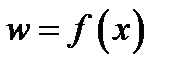Довольно часто при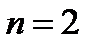 
функцию многих переменных 
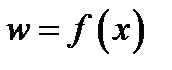записывают в виде 
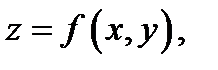а при 
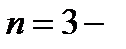в виде 
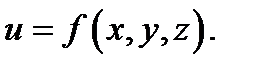При 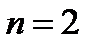множество точек 
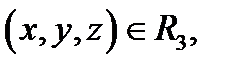удовлетворяющих уравнению 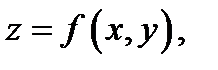именуется графиком функции двух переменных 
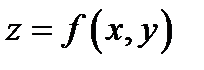(см. Р.2). Увидим, что при аналитической записи 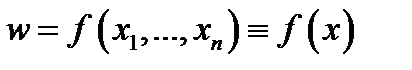функции нескольких переменных под областью определения знают естественную область определе-
ния данной функции, т.е. множество доводов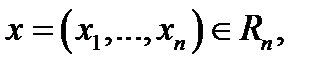 
при которых выражение 
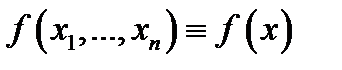имеет суть (возможно вычислено). К примеру, областью определения функции 
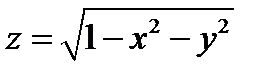яляется множество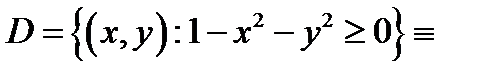 
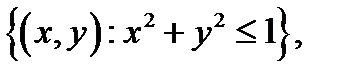т.е. замкнутый круг радиуса, равного единице.
Замечание 1.При изображении области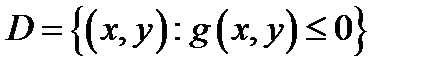 
на плоскости 
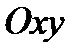рисуют кривую 
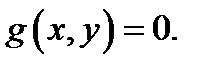Пускай эта кривая несложная, т.е. постоянна и без точек самопересечения. Тогда берут произвольную точку 
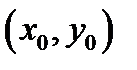и подставляют её в 
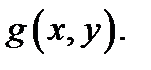В случае, если 
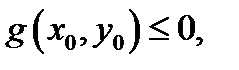то эта точка и все точки 
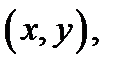находящиеся на кривой 
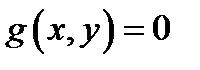и по одну сторону от неё, будут лежать в области 
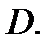Это правило действует и в том случае, в то время, когда уравнение 
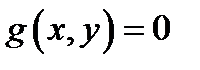задаёт на плоскости пара несложных кривых.
График функции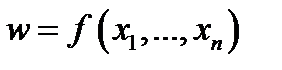 
нереально изобразить, в случае, если число свободных переменных больше двух. Но при функции 
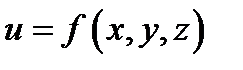трех переменных возможно привлечь кое-какие геометрические иллюстрации. Поверхность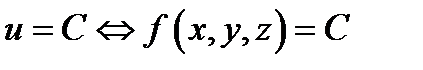 
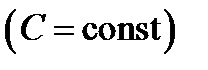в трехмерном пространстве 
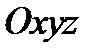именуется поверхностью уровня функции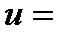 
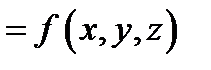. Изменяя постоянную 
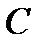, возможно визуально себе представить все подробности поверхности 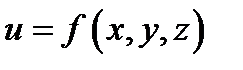в плоскости 
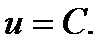При функции 
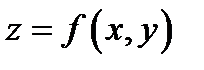двух переменных линии 
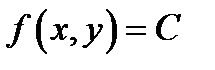являются плоскими кривыми, именуемыми линиями уров-
ня. Ими пользуются при, в то время, когда объёмную фигуру желают изобразить на плоскости. К примеру, при составлении географических карт, гора (бугор) изображается в виде семейства линий уровня с ответвлениями во вне маленьких отрезков, а впадины – с ответвлениям во вовнутрь маленьких отрезков ( посмотрите эти изображения на любой географической карте).
Дадим сейчас непрерывности функции и понятия предела многих переменных. Потому, что эти определения подобны определениям функции одной переменной, то сделаем это коротко. Пускай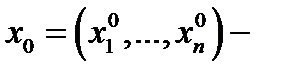 
предельная точка множеств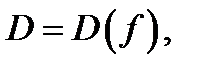а 
а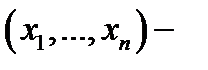 
произвольная точка пространства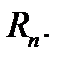 
Определение 3.Следующее высказывание есть определением предела функции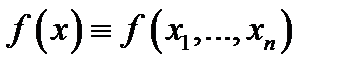 
в точке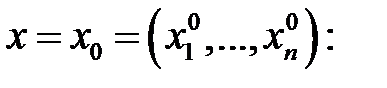 
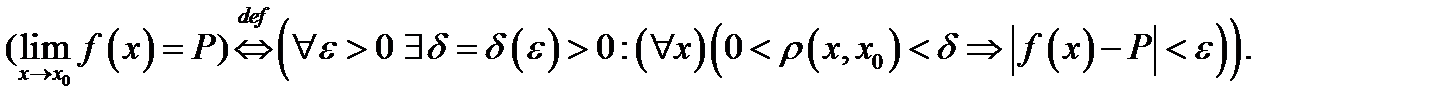[1]
Определение 4.Функция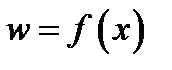 
именуется постоянной в точке 
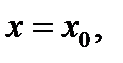в случае, если 
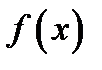выяснена в точке 
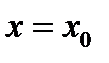и некоей её окрестности и в случае, если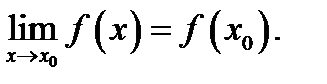 
Для функции двух переменных определение предела записывается так:
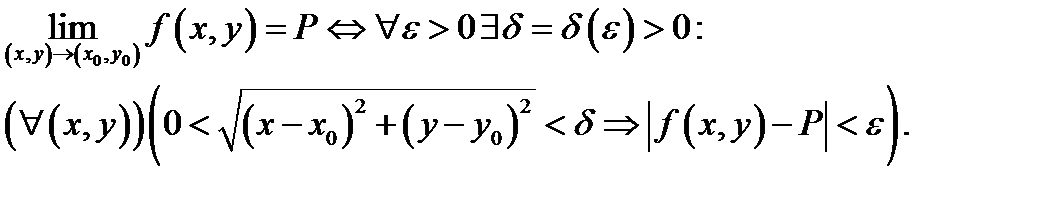
Из этого следует, что в случае, если предел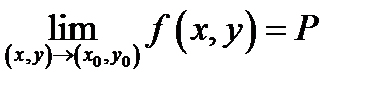 
существует, то он не зависит от того, по какому пути точка 
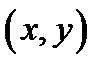пытается к предельной точке 
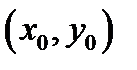(см. Р.3).В случае, если найдутся два разных дороги, по которым указанный предел имеет разные значения, то 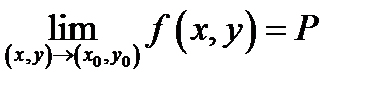не существует.
Увидим, что все теоремы об арифметических действиях над непрерывными функциями и пределами, и теоремы о переходе к пределу под знаком постоянной функции непрерывности сложной функции и теорема о символе предела, сформулированные для функций одной переменной, очевидным образом переносятся на функции многих переменных (рекомендуем записать соответствующие формулировки в качестве упражнения).
Ответ.Перейдем к полярным координатам посредством форомул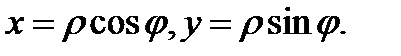 
Тогда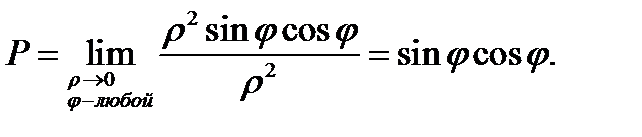 
В случае, если точка 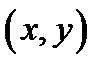пытается к точке 
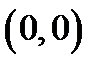по пути 
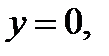то 
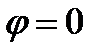и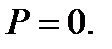 
В случае, если 
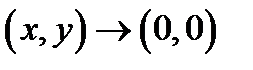по пути 
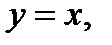то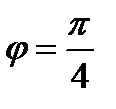 
и тогда 
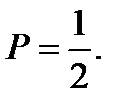Так, по двум разным дорогам, ведущим в точку 
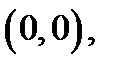разглядываемый предел оказал-
ся разным. Следовательно, предел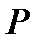 
не существует.
Выписанные ниже пределы
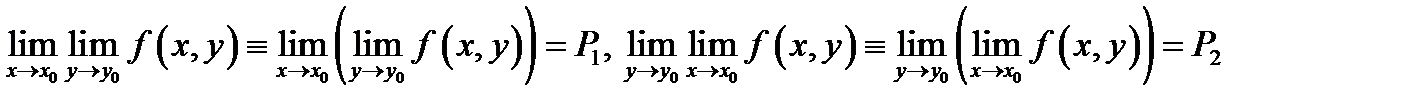
именуются повторными пределами функции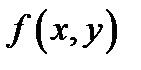 
в точке 
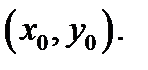Они смогут не совпадать между собой.
Теорема 1.Пускай существует простой предел 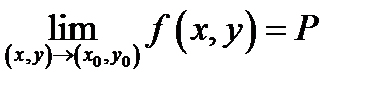и пускай при любом фиксированном 
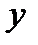из некоей окрестности точки 
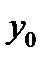существует предел 
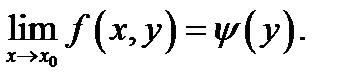Тогда существует и повторный предел 
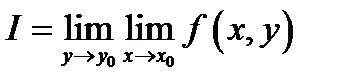и он равен двойному пределу 
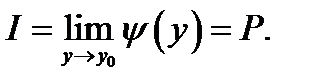В случае, если, помимо этого, при каждом 
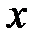из некоей окрестности точки 
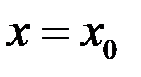существует предел 
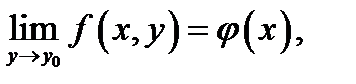то
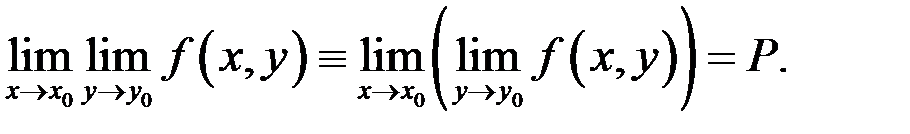
Введем сейчас понятие элементарной функции нескольких переменных. Понятие простейщей элементарной функции одной переменной было дано в прошлом семестре. Составим сейчас таблицу всех несложных элементарных функций по каждой из переменных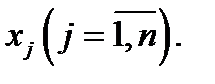 
Тогда функция 
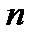переменных 
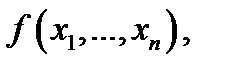полученная из функций указанной таблицы путём применения к ним взятия функции и 
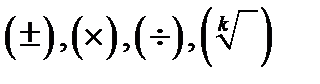конечного числа операций от функции (образования сложных функций), именуется элементарной функцией 
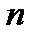переменных 
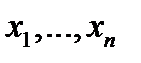(неспециализированного вида).
Применяя теоремы об арифметических действиях над пределами и пределе сложной функции, докажем следующий итог.
Теорема 2.Каждая элементарная функция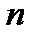 
переменных постоянна в любой внутрен-
ней точке собственной области определения.
К примеру, функция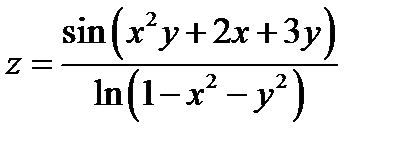 
есть элементарной с областью определения
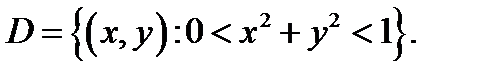Все точки этого множества – внутренние, исходя из этого эта функция постоянна в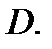 
Потому, что все результаты, касающиеся функций двух переменных, очевидным образом переносятся и на функции бо?льшего числа переменных, то предстоящее изложение материала
будем давать для функций двух переменных.
Перейдем к изложению дифференциального исчисления функций многих переменных. Пускай функция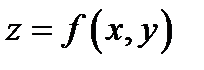 
выяснена в точке 
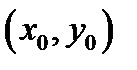и некоей её окрестности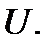 
Определение 3.Пределы
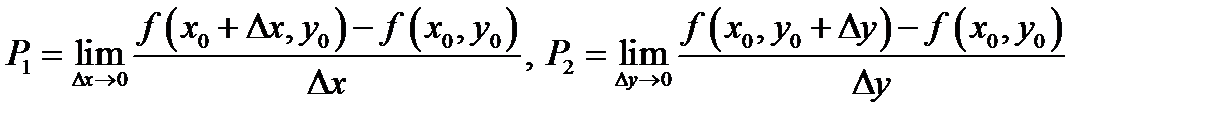
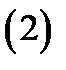
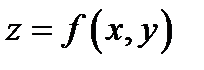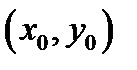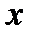(если они существуют и конечны) именуются частными производными функции в точке по 
и по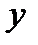 
соответственно и обозначаются
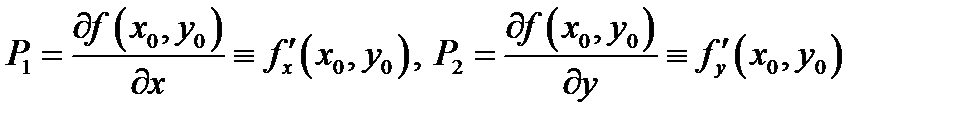
(довольно часто штрихи опускают и пишут легко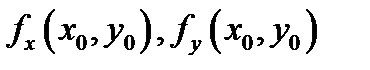 
).
Геометрический суть частных производных пребывает в следующем. Совершим плоскость
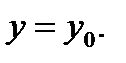Она вырежет из поверхности 
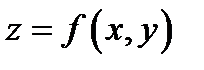кривую (см. Р.4)
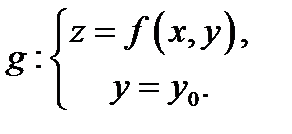
Угловой коэффициент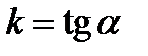 
данной кривой в точке 
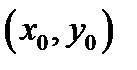будет равен 
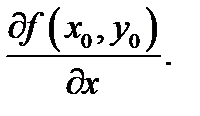И подобно, личная производная 
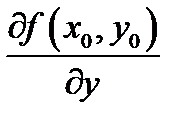есть угловым коэффициентом кривой
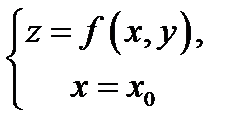
в точке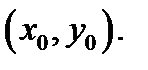 
Из определения 3 вытекает, что для вычисления личной производной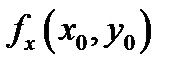 
нужно зафиксировать переменную 
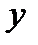(сделать ее параметром) и забрать простую производную по 
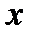как функции одной переменной. Подобное замечание справедливо и по отношению к личной производной 
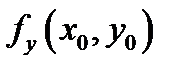. К примеру, 
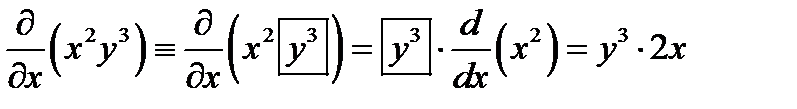(тут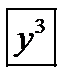 
свидетельствует, что переменная 
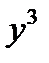фиксируется). И подобно,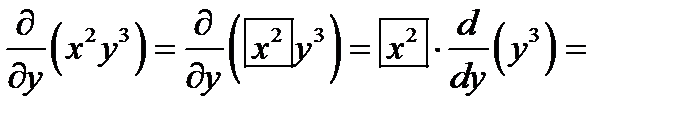 
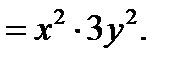
3. Дифференцируемость функций многих переменных, сообщение с частными производными. Полный дифференциал. Достаточное условие дифференцируемости
Для функции одной переменной дифференцируемость равносильно существованию конечной производной. Для функций многих переменных это не верно. Перейдем к разъяснению этого факта.
Определение 4.Говорят, что функция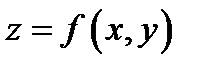 
(определенная в точке 
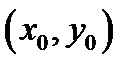и некоей её окрестности) дифференцируема в точке 
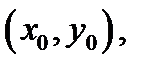в случае, если её полное приращение 
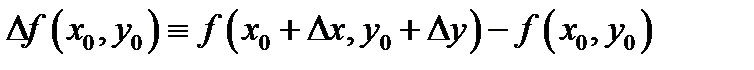в данной точке возможно представлено в виде
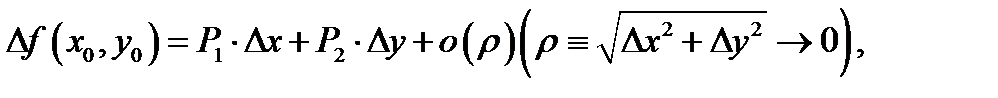
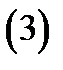
где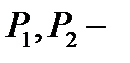 
числа, не зависящие от 
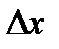и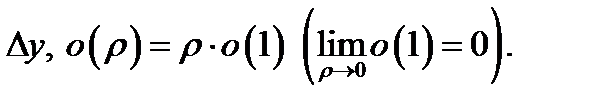 
Наряду с этим линейная часть 
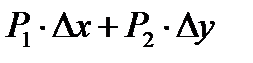приращения (3) именуется дифференциалом функции 
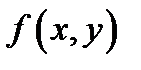в точке 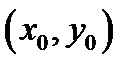и обозначается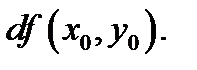 
Теорема 3 (нужное условие дифференцируемости).В случае, если функция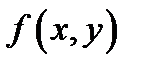 
дифференцируема в точке 
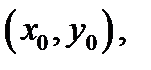то она постоянна в данной точке и имеет в ней частные производные, причем 
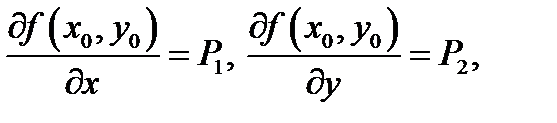где 
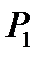и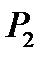 
совпадают с числами, указанными в (3). Наряду с этим [2]
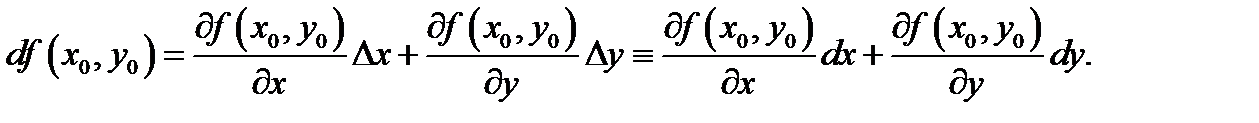
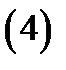
Подтверждение.Пускай 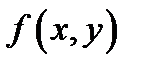дифференцируема в точке 
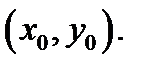Тогда имеет место представление (3), верное для любых приращений 
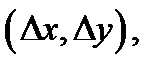только бы 
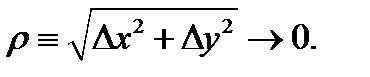Значит, оно правильно в частности и для приращений 
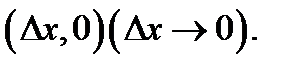Для таких приращений соотношение (3) записывается в виде
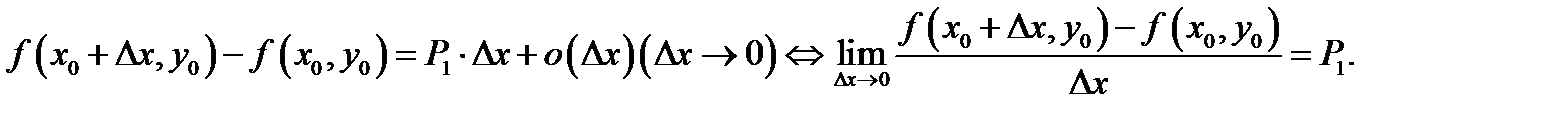
Это указывает, что существует личная производная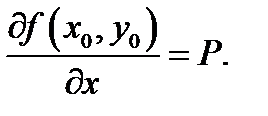 
Забрав приращения вида 
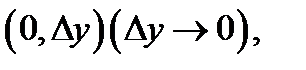возьмём, что существует личная производная 
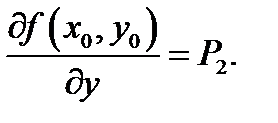И, наконец, в случае, если
в (3) перейти к пределу при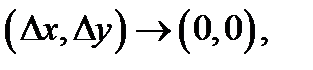 
то возьмём, что 
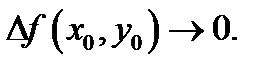Это указывает, что функция 
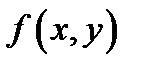постоянна в точке 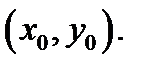Теорема доказана.
Замечание 2. Из существования частных производных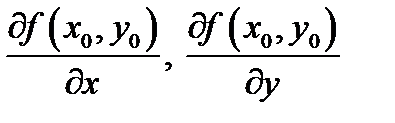 
не вытекает дифференцируемость функции 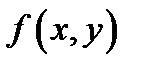в точке 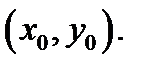К примеру, для функции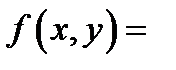 
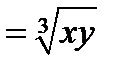частные производные jсуществуют и равны нулю, но эта функция не есть дифференцируемой в точке 
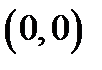(докажите это в качестве упражнения).
Теорема 4 (достаточные условия дифференцируемости).Пускай функция 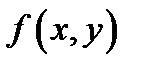имеет в точке 
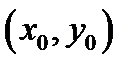и некоей её окрестности частные производные 
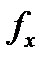и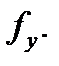 
В случае, если эти производные постоянны в точке 
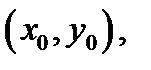то функция 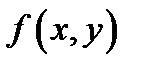дифференцируема в точке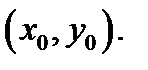 
Упражнение 1.Продемонстрируйте, что функция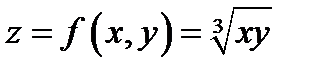 
имеет в точке 
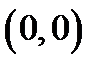и некото-рой её окрестности частные производные 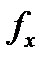и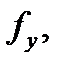 
но они не являются постоянными в ука-
занной точке(исходя из этого дифференцируемость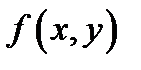 
в точке 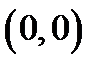нельзя гарантировать).