М К Э
Лекция 1. Способ Галёркина
Об ортогональности функций
Пускай ? область трансформации , а ? функции, определенные в . Через обозначим класс этих функций.
а) В случае, если . Обозначение: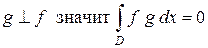 
.
б) Пускай ? полная в совокупность базовых функций. Тогда каждая функция представима в виде разложения по базису
,
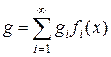где коэффициенты определяются конкретно. Базовые функции линейно свободны, т.е. из равенства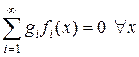 
направляться, что все коэффициенты равны нулю. Но тогда и . Итак, в случае, если функция ортогональна совокупности базовых функций, то она тождественно равна нулю.
Способ взвешенных невязок
Разглядим уравнение
. (1.1)
Пускай ? приближение к ответу уравнения (1). Обозначим через
(1.2)
невязку уравнения (1) на этом приближенном ответе. Пускай, потом, ? совокупность базовых функций. Тогда возможно записать
.
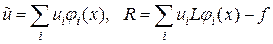Дабы отыскать коэффициенты , потребуем, дабы невязка была ортогональна некоей совокупности весовых функций , т.е.
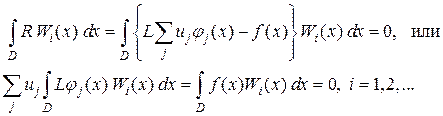(1.3)
Способ Галеркина
Галеркин применял базовые функции вместо весовых, что ведет к следующей совокупности линейных уравнений относительно искомых коэффициентов разложения
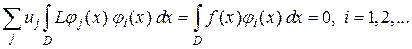
либо
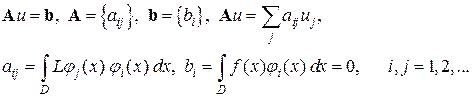(1.4)
Замечание. В конечномерном пространстве , и совокупность уравнений (4) делается конечной.
Пример применения способа Галеркина.
Решим задачу
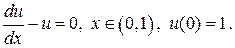(1.5)
Правильное ответ данной задачи разумеется: . Выберем совокупность базовых функций
(1.6)
и представим ответ в виде разложения по базису,
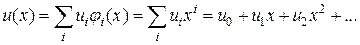. (1.7)
В разложении (7) искомыми являются коэффициенты . Полагая , находим . Пускай , тогда осталось отыскать . Подставим (1.7) в (1.5) и вычислим невязку
.
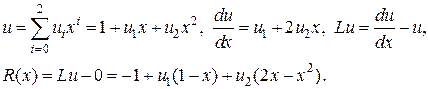Потребуем, дабы невязка была ортогональна базовым функциям: . Возьмём совокупность уравнений
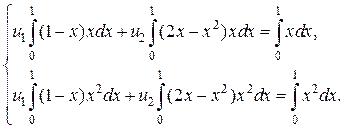
Вычислим интегралы и возьмём
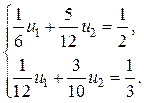
Ответ данной совокупности таково: , а приближенное ответ (7) задачи (5) имеется парабола
.
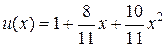График данной функции в сравнении с правильным ответом продемонстрирован на рисунке
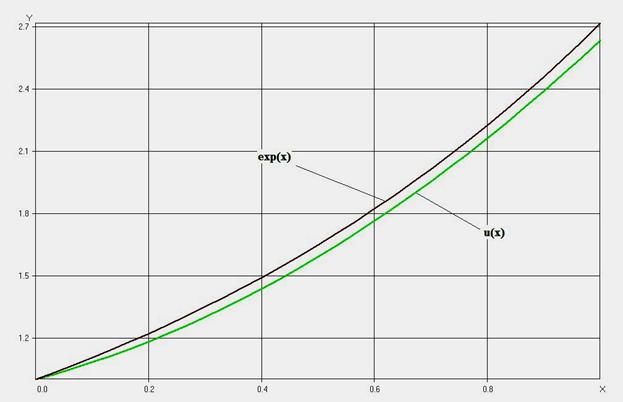
Рис. 1.1. Правильное и приближенное ответ задачи (1.5) способом Галеркина при N=2.
Упражнение 1. Решить задачу (1.5) при N=3, сравнить с ответом для N=2.
Лекция 3. Совокупность уравнений МКЭ
Сетка МКЭ
Покроем область сеткой конечных элементов , , так дабы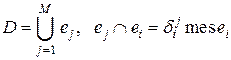 
.
Тогда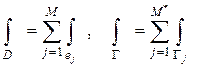 
. Звёздочка свидетельствует, что при интегрировании по границе в сумму входят только те конечные элементы , границы которых не смотря на то, что частично лежат на границе области .
Разглядим отдельный конечный элемент. К примеру, это многоугольник. Пускай он имеет узлов. Тогда возможно ввести базовые функции этого элемента . Эти функции линейно свободны и нормированы так, что . Произвольная функция на элементе возможно представлена разложением по базису
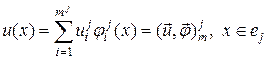(3.1)
Индекс обозначает принадлежность к -му элементу. В будущем, в случае, если это не ведет к недоразумениям, индекс довольно часто будем опускать. Индекс употребляется для локальной нумерации узлов конечного элемента. направляться подчернуть, что локальные узлы элемента смогут совпадать с вершинами многоугольника , а смогут и не совпадать с ними, как продемонстрировано на рис. 3.1. Наровне с локальной вводят сквозную глобальную нумерацию узлов. Соответствие локальных и глобальных номеров, их координаты, и связность (т.е. указание, какие конкретно узлы образуют элемент) задаётся посредством двух главных таблиц, каковые воображают МКЭ-сетку.
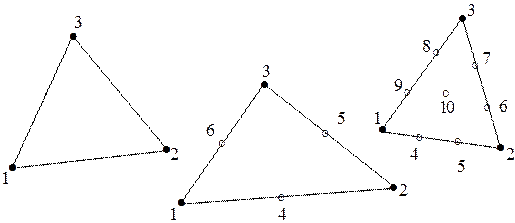
Рис. 3.1. Трехузловой, шестиузловой и десятиузловой
треугольные конечные элементы
Таблица 1. Узлы
| № | x | y | b | z |
| i | ||||
| N |
Поле (bound) употребляется, дабы отличить внутренние узлы ( ) от граничных ( ). Показатель разрешает в программе, применяющей эту сетку, задавать необходимое граничное условие; к примеру, в случае, если , ? то это условие Дирихле, в случае, если , ? то ставится условие Неймана, и т.д. на различных участках границы . Поле (zone) употребляется, дабы задавать разные функции для коэффициентов решаемой задачи; к примеру, коэффициент теплопроводности в композитных материалах: ? сталь, ? алюминий и т.д.
Таблица 1 не разрешает нарисовать МКЭ-сетку, а лишь узлы. Это значит, что требуется еще одна таблица элементов, либо таблица связности, в которой указывались бы связи узлов ребрами да и то, какие конкретно узлы образуют элемент.
Таблица 2. Элементы
| № | n1 | n2 | n3 | … | nm | z |
| направляться | ||||||
| M |
Строчок таблицы элементов говорит о том, что конечный элемент ? это треугольник с вершинами в узлах 213, 45 и 41246 и расположенный в зоне 3. Так, эта таблица показывает соответствие локальных и глобальных номеров узлов. Наряду с этим локальный порядок нумерации выяснен заблаговременно, к примеру как продемонстрировано на рис. 3.1. Принято, дабы «главные» узлы элемента, т.е. узлы, совпадающие с вершинами многоугольника, нумеровались против хода часовой стрелки.
Посредством двух элементов – и таблиц узлов – легко нарисовать МКЭ-сетку. Для этого в цикле рисуем любой элемент. Конечный элемент рисуется так: в строчке таблицы 2 последовательно берутся глобальные номера , для каждого из них в строчках таблицы 1 берутся координаты и узлы соединяются ребрами в порядке . Так, элементов и таблицы узлов конкретно определяют МКЭ-сетку.
Замечание. На практике наровне с этими таблицами комфортно пользоваться таблицами инцидентности (либо таблицами соседей). Так, для фрагмента сетки, продемонстрированной на рис. 3.2 таблицы 3, 4 элементов и инцидентных узлов выглядят так (заполнены лишь 1-я и 19-я строки)
Рис. 3.2. Фрагмент МКЭ-сетки
Таблица 3. Инцидентные узлы
| № | e1 | e2 | e3 | e4 | e5 | e6 | … | ep |
| N |
Таблица 4. Инцидентные элементы
| № | k1 | k2 | k3 | k4 | k5 | k6 | … | kz |
| N |
Билинейный элемент
Пускай сетка складывается из четырехугольников, см. рис. 1.
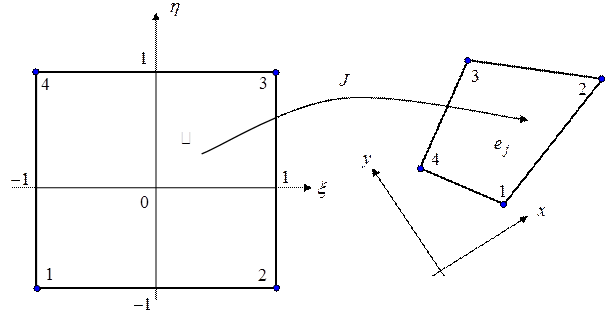
Рис. 1 Базовый квадрат и четырехугольный элемент сетки
Введем базовый квадрат и определим преобразование актуальных координат в локальные :
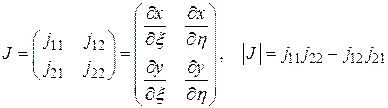(1)
На базовом квадрате введем базовые функции , и выразим через них преобразование координат :
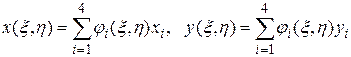(2)
Функции комфортно строить посредством интерполянтов Лагранжа
, (**)
то есть
(3)
Дифференцирование
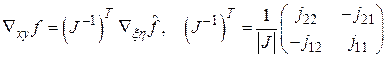(4)
Интегрирование
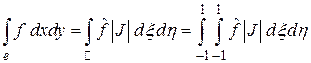(5)
Вычислим элементы матрицы Якоби посредством формул (2) – (4).
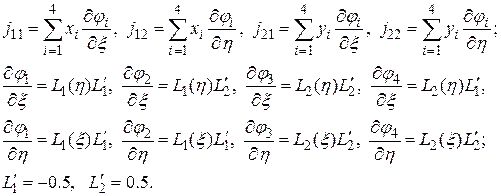(6)
Сейчас возможно подсчитать градиент (4) функции , предварительно разложив по базизу в , то есть, записав
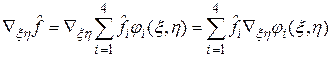. (7)
Ко мне входят градиенты базовых функций и вычислим градиенты . Дабы вычислить их, подставим (**) в (6). Возьмём
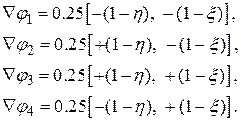(8)
Итак, (7) + (8) определяют операцию дифференцирования. А подстановка (8) в (2) и после этого в (1) разрешает отыскать все элементы матрицы Якоби. К примеру,
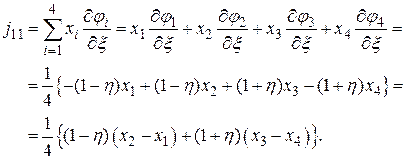
Совершенно верно кроме этого отыщем
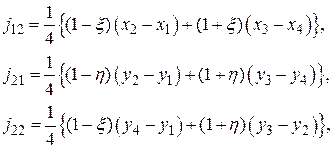(9)
Лекция 5. Введение в М К О
Базы метода
Требуется решить задачу в области , где ? дифференциальный оператор, ? заданная функция.
Примеры.
1) Стационарное уравнение теплопроводности
(5.1)
2) Нестационарное уравнение теплопроводности. Полудискретизованная неявная схема по времени с шагом
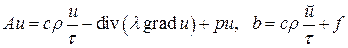(5.2)
Возможно и умножить все на и поделить на .
3) Конвективная теплопроводность, схема явная по конвекции
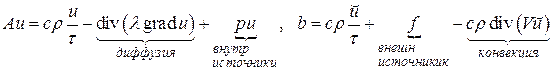(5.3)
Как решать? МКО: покрыть непересекающимися конечными количествами, 
? конечный количество.
Примеры.
1) 1D.
2) 2D cтруктурированная
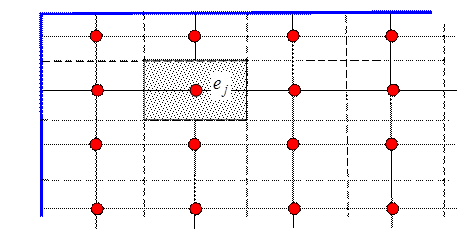
3) 2D неструктурированная
Интегрируем уравнение (5.3) по с границей
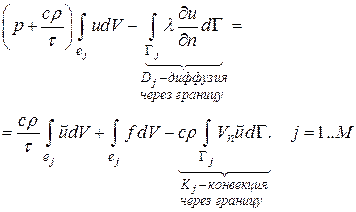(5.4)
Тут ? внешняя нормаль к границе .
Консервативность МКО.
В случае, если сложить все уравнение (5.4), то интегралы по всем внутренним границам КО взаимно уничтожатся, т.к. эти границы попарно-смежные, и нормали у пар направлены противоположно. Останутся только интегралы по внешним участкам границы . Будем иметь
,
,
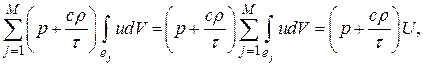
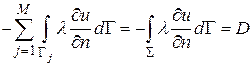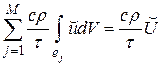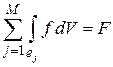
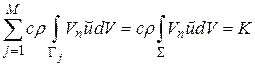
Совсем имеем закон сохранения энергии
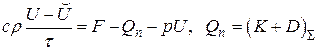
Возвратимся к совокупности уравнений (5.4), чтобы получить из него СЛАУ довольно узловых значений. Для этого нужна какая-то аппроксимация при вычислении интегралов в (5.4). В большинстве случаев, в то время, когда с каждым КО связан один узел , полагают
,
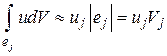где ? количество элемента . Так вычисляются все интегралы по КО от функций. Сложнее дело обстоит с вычислением потоков и через границу, т.е. выражение этих потоков через узловые значения . Этим и различаются одни схемы МКО от вторых. Принципиально важно соблюдение следующего правила: для каждой пары смежных внутренних границ КО потоки имеют одно значение, но различаются знаком (конкретно из этого направляться консервативность всей схемы).
М К Э
Лекция 1. Способ Галёркина
Об ортогональности функций
Пускай ? область трансформации , а ? функции, определенные в . Через обозначим класс этих функций.
а) В случае, если . Обозначение: .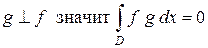
б) Пускай ? полная в совокупность базовых функций. Тогда каждая функция представима в виде разложения по базису
,
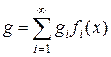где коэффициенты определяются конкретно. Базовые функции линейно свободны, т.е. из равенства 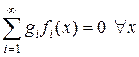направляться, что все коэффициенты равны нулю. Но тогда и . Итак, в случае, если функция ортогональна совокупности базовых функций, то она тождественно равна нулю.
Способ взвешенных невязок
Разглядим уравнение
. (1.1)
Пускай ? приближение к ответу уравнения (1). Обозначим через
(1.2)
невязку уравнения (1) на этом приближенном ответе. Пускай, потом, ? совокупность базовых функций. Тогда возможно записать
.
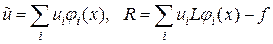Дабы отыскать коэффициенты , потребуем, дабы невязка была ортогональна некоей совокупности весовых функций , т.е.
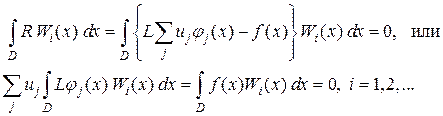(1.3)
Способ Галеркина
Галеркин применял базовые функции вместо весовых, что ведет к следующей совокупности линейных уравнений относительно искомых коэффициентов разложения
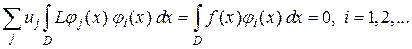
либо
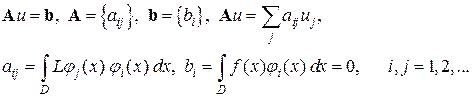(1.4)
Замечание. В конечномерном пространстве , и совокупность уравнений (4) делается конечной.
Пример применения способа Галеркина.
Решим задачу
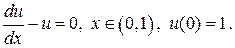(1.5)
Правильное ответ данной задачи разумеется: . Выберем совокупность базовых функций
(1.6)
и представим ответ в виде разложения по базису,
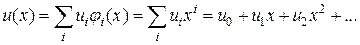. (1.7)
В разложении (7) искомыми являются коэффициенты . Полагая , находим . Пускай , тогда осталось отыскать . Подставим (1.7) в (1.5) и вычислим невязку
.
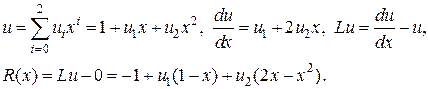Потребуем, дабы невязка была ортогональна базовым функциям: . Возьмём совокупность уравнений
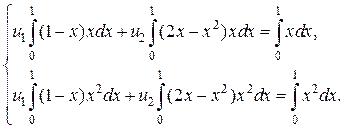
Вычислим интегралы и возьмём
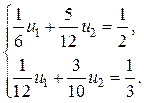
Ответ данной совокупности таково: , а приближенное ответ (7) задачи (5) имеется парабола
.
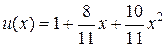График данной функции в сравнении с правильным ответом продемонстрирован на рисунке
Рис. 1.1. Правильное и приближенное ответ задачи (1.5) способом Галеркина при N=2.
Упражнение 1. Решить задачу (1.5) при N=3, сравнить с ответом для N=2.
Базовые функции с конечным носителем
До сих пор мы разглядывали базовые функции, определенные везде в . Довольно часто таковой выбор неудобен; к примеру при выборе при громадном получаются полиномы большого порядка, что затрудняет вычисления. В МКЭ в большинстве случаев используют базовые функции с конечным носителем, что связан с триангуляцией области, т.е. с ее сеточным разбиением на конечные элементы. Разглядим несложный пример равномерной сетки на отрезке с узлами Для каждого узла определим т.н. пирамидальную базовую функцию
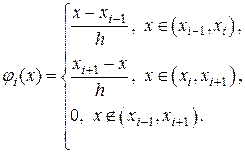(1.8)
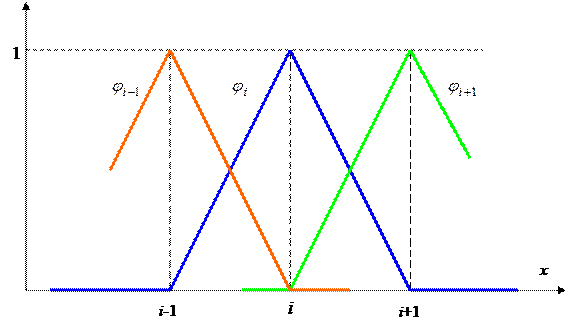Рис. 1.2. Пирамидальные базовые функции
Увидим, что
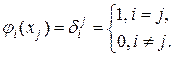(1.9)
Исходя из этого, во-первых, такая совокупность базовых функций линейно-свободна, а во-вторых, коэффициенты разложения (1.7) любой функции по этому базису будут равны значениям функции в узлах сетки, .
Лекция 2. не сильный (обобщенная) форма постановки краевых задач
для дифференциальных уравнений
Пускай ? дифференциальный оператор, и требуется решить задачу . Умножим это уравнение на произвольную пробную функцию и проинтегрируем по области . Возьмём
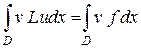(2.1)
Это уравнение должно выполняться . Оно именуется не сильный формой исходного дифференциального уравнения. Идейно не сильный форма (2.1) связана с подходом Галеркина либо способом взвешенных невязок, потому, что возможно представлена в виде
.
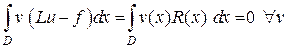Довольно часто при записи обобщенных формулировок задач вместо интегралов применяют эквивалентный знак скалярного произведения:
(2.2)
Чтобы получить из (2.1) либо (2.2) совокупность уравнений для узловых значений, достаточно
1) совершить триангуляцию области;
2) выбрать ассоциированную с триангуляцией конечную совокупность базовых функций, владеющую свойством (1.9);
3) записать способ Галеркина ( )
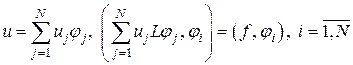(2.3)
либо
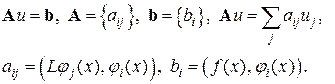(2.4)
Пример применения базовых функций с конечным носителем.
Решим задачу теплопроводности
. (2.5)
Правильное ответ задачи (2.5) имеет форму .
;
выберем пирамидальные базовые функции (1.8) и подсчитаем их производные:
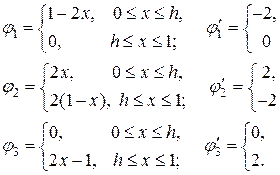(2.6)
Применяя представление приближенного ответа
(2.7)
и граничные условия в точках и , приобретаем
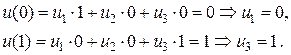
Так, осталось отыскать коэффициент . Для этого достаточно выяснить вторую строчок совокупности уравнений (2.4), то есть коэффициенты . Яркое использование формул (2.4) для вычисления нереально, потому, что предполагает вычисления вторых производных от линейных базовых функций (2.6). Это отражает очевидный факт, что линейные функции не могут служить базисом в классе два раза дифференцируемых функций, у которого в собствености ответ исходной дифференциальной задачи. Но в случае, если ослабить требование гладкости, то посредством формулы интегрирования по частям возможно записать
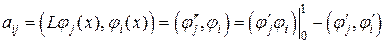(2.8)
В правую часть формулы (2.8) сейчас входят только первые производные базовых функций, каковые выяснены в (2.6). Наряду с этим, не обращая внимания на то, что производные терпят разрыв в узлах сетки, возможно вычислить
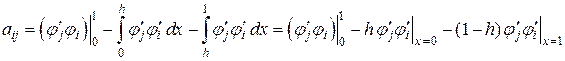(2.9)
Увидим, что для интересующих нас коэффициентов подстановка в правой части (2.9) равна нулю, т.к. . Совсем при возьмём формулу
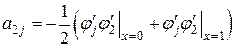(2.10)
Подставляя в (2.10) необходимые значения производных из (2.6), отыщем , , . Правая часть уравнения вычисляется интегрированием
.
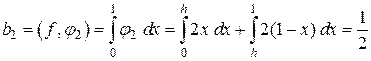Итак, второе уравнение совокупности уравнений для определения коэффициентов разложения имеет форму
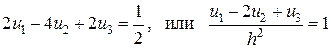. (2.11)
Нетрудно видеть, что уравнение (2.11) сходится с конечно-разностной аппроксимацией исходного уравнения в центральном узле сетки.
Ранее посредством граничных условий было обнаружено, что , так что из (2.11) легко отыскать . Совсем приближенное ответ задачи способом Галёркина имеет форму
.
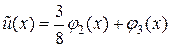На рисунке продемонстрирован график данной функции в сравнении с правильным ответом .
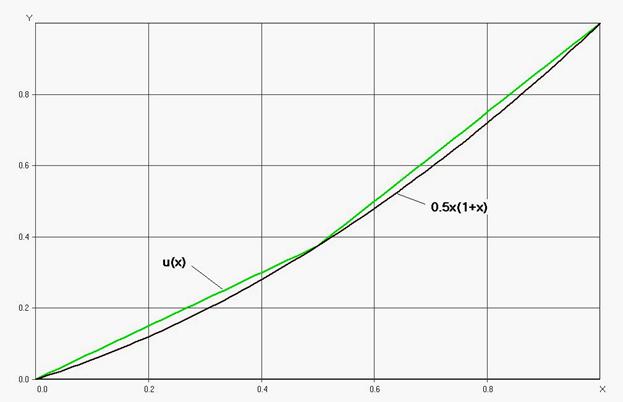
Рис. 2.1. Правильное и приближенное ответ МКЭ задачи (2.5) при N=3
Упражнение 2. Решить задачу (2.5) при N=4, сравнить с ответом для N=3.