Обоюдное размещение прямых в пространстве
Разглядим две прямые, записанные в каноническом виде
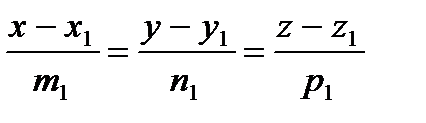 и
и 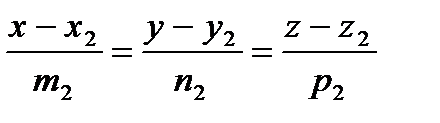 ,
,
где 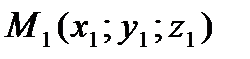 и
и 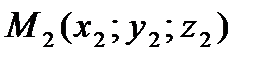 – точки, находящиеся в собствености этим прямым, а
– точки, находящиеся в собствености этим прямым, а 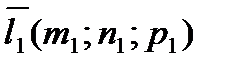 и
и 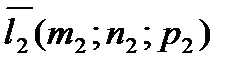 – направляющие векторы этих прямых.
– направляющие векторы этих прямых.
1. Прямые параллельны, в случае, если параллельны их направляющие векторы:
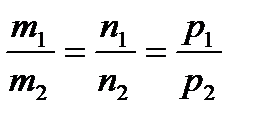 . (5.13)
. (5.13)
Но направляющие векторы прямых не должны быть параллельны вектору 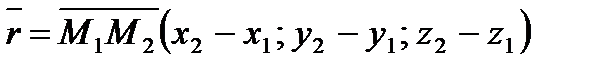 .
.
2. Прямые перпендикулярны, в случае, если перпендикулярны их направляющие векторы:
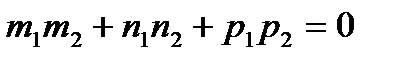 (5.14)
(5.14)
3. В случае, если прямые образуют угол 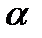 , то
, то
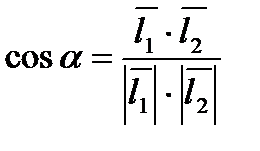 . (5.15)
. (5.15)
4. Прямые скрещиваются, если они лежат в различных плоскостях, другими словами векторы 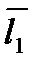 ,
, 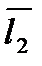 и
и 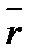 не компланарны:
не компланарны:
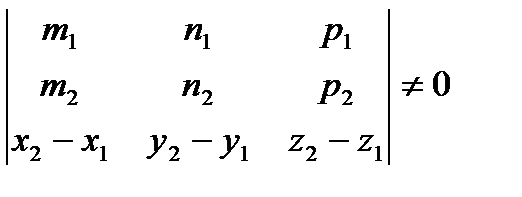 . (5.16)
. (5.16)
Пример 9. Установите обоюдное размещение прямых 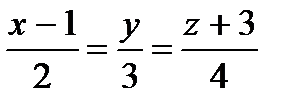 и
и 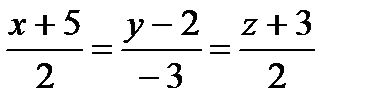 .
.
Ответ. 1. В соответствии с условию запишем: 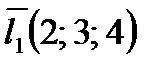 ,
, 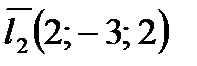 ,
, 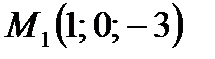 ,
, 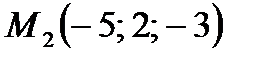 .
.
2. Узнаем, являются ли прямые параллельными: 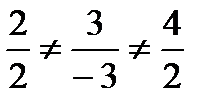 . Так как не выполняется условие 5.13, то эти прямые не параллельны.
. Так как не выполняется условие 5.13, то эти прямые не параллельны.
3. Узнаем, являются ли прямые скрещивающимися:
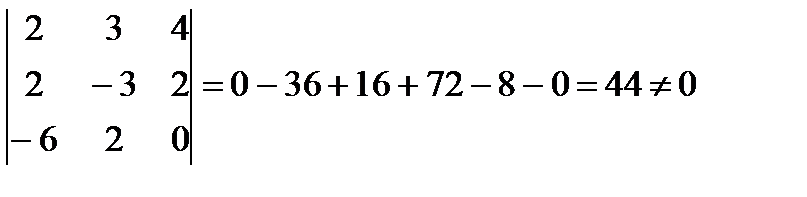 .
.
Так как выполняется условие 5.16, то эти прямые скрещиваются.
Ответ: прямые скрещиваются.
Пример 10. Отыщите угол между прямыми 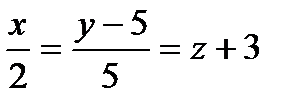 и
и 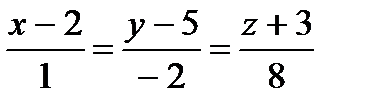 .
.
Ответ. 1. Запишем направляющие векторы этих прямых:
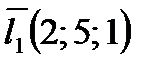 и
и 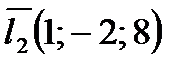 .
.
2. Отыщем скалярное произведение направляющих векторов:
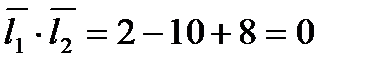 .
.
Так как эти прямые перпендикулярны, то 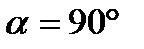 .
.
Ответ: 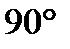 .
.
плоскости и Взаимное расположение прямой
Разглядим плоскость 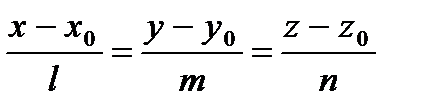 и прямую
и прямую 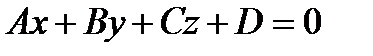 .
.
1. Прямая параллельна плоскости, в случае, если
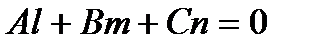 . (5.17)
. (5.17)
2. Прямая перпендикулярна плоскости, в случае, если
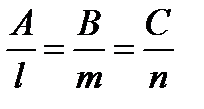 . (5.18)
. (5.18)
3. В случае, если прямая образует с плоскостью угол 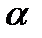 , то
, то
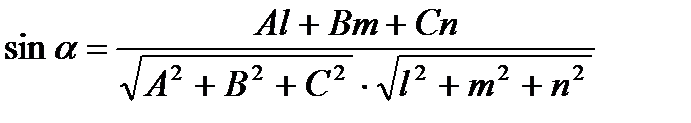 . (5.19)
. (5.19)
Пример 11. Определите значение p, при котором прямая 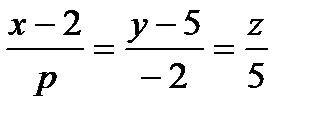 параллельна плоскости
параллельна плоскости 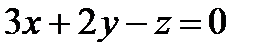 .
.
Ответ. В соответствии с условию задачи запишем:
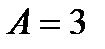 ,
, 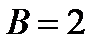 ,
, 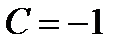 ,
, 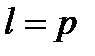 ,
, 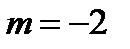 ,
, 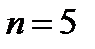 .
.
Подставляя эти значения в формулу 5.17, возьмём:
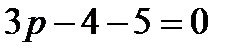 , откуда
, откуда 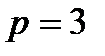 .
.
Ответ: 3.
Расстояние от точки до плоскости
Расстояние от точки 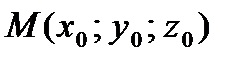 до плоскости
до плоскости
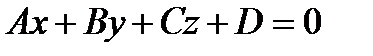
с обычным вектором 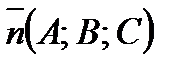 находят по формуле:
находят по формуле:
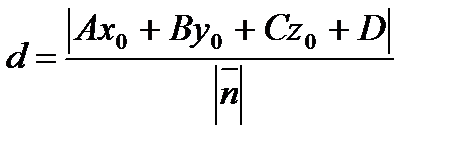 . (5.20)
. (5.20)
Пример 12. Отыщите расстояние между плоскостями 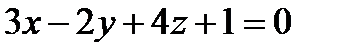 и
и 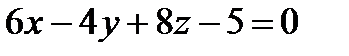 .
.
Ответ. 1. Эти плоскости параллельны, поскольку выполняется условие 5.6: 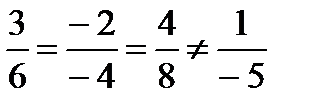 .
.
2. Отыщем любую точку, принадлежащую первой плоскости. К примеру, полагая 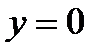 , а
, а 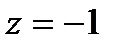 , возьмём
, возьмём 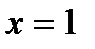 .
.
2. Отыщем расстояние от точки 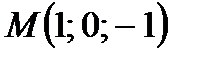 до плоскости
до плоскости 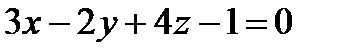 . В соответствии с формуле 5.20 запишем:
. В соответствии с формуле 5.20 запишем:
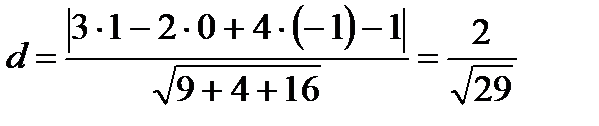 .
.
Ответ: 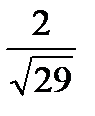 .
.
Контрольный тест 5
Укажите верный вариант ответа (1 – 10):
1. В случае, если точка 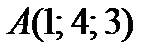 в собственности плоскости
в собственности плоскости
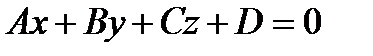 ,
,
а вектор 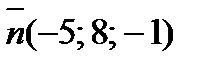 – обычный вектор данной плоскости, то значение D равняется
– обычный вектор данной плоскости, то значение D равняется
Варианты ответов: 1) 0; 2) 14; 3) – 8; 4) – 24; 5) 24.
2. В случае, если плоскость проходит через точки 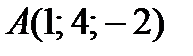 ,
, 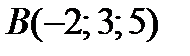 и
и 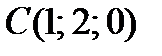 , то сумма координат обычного вектора данной плоскости равна
, то сумма координат обычного вектора данной плоскости равна
Варианты ответов: 1) 4; 2) 9; 3) 0; 4) – 4; 5) 17.
3.В случае, если 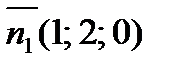 – обычный вектор плоскости
– обычный вектор плоскости 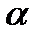 , а
, а 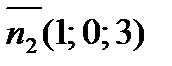 – обычный вектор плоскости
– обычный вектор плоскости 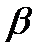 , то угол между этими плоскостями равен
, то угол между этими плоскостями равен
Варианты ответов: 1) 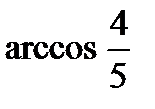 ; 2)
; 2) 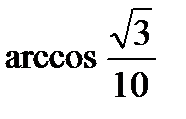 ; 3)
; 3) 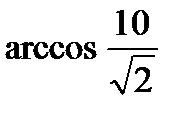 ; 4)
; 4) 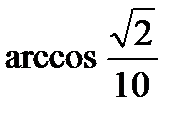 ; 5)
; 5) 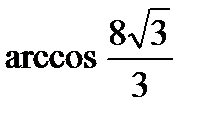 .
.
4. Расстояние от точки 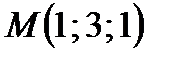 до плоскости
до плоскости 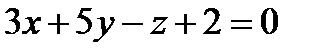 равняется
равняется
Варианты ответов:
1) 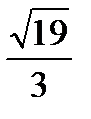 ; 2)
; 2) 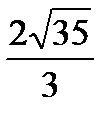 ; 3)
; 3) 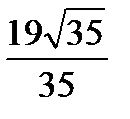 ; 4)
; 4) 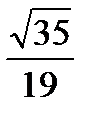 ; 5)
; 5) 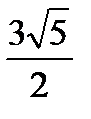 .
.
5.Плоскости 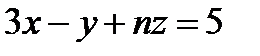 и
и 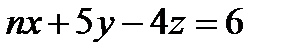 перпендикулярны при условии, что значение n равняется
перпендикулярны при условии, что значение n равняется
Варианты ответов: 1) – 2; 2) 1; 3) 0; 4) 4; 5) – 5.
6.В случае, если прямая 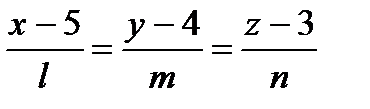 параллельна вектору
параллельна вектору 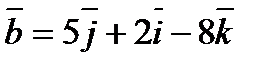 и проходит через точку
и проходит через точку 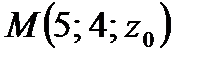 , то значение выражения
, то значение выражения 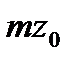 равняется
равняется
Варианты ответов: 1) 10; 2) 15; 3) – 24; 4) 24; 5) – 6.
7.В случае, если прямая перпендикулярна векторам 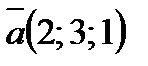 и
и 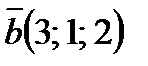 , то она параллельна вектору
, то она параллельна вектору
Варианты ответов: 1) 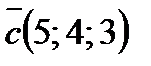 ; 2)
; 2) 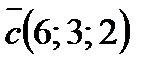 ; 3)
; 3) 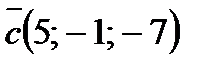 ; 4)
; 4) 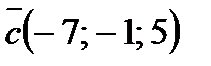 ; 5)
; 5) 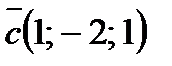 .
.
8. В случае, если точки 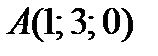 ,
, 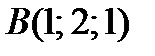 ,
, 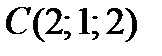 и
и 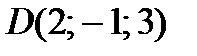 – вершины пирамиды, то безотносительная величина скалярного произведения обычных векторов граней ABC и ADC равна
– вершины пирамиды, то безотносительная величина скалярного произведения обычных векторов граней ABC и ADC равна
Варианты ответов: 1) 3; 2) 0; 3) 1; 4) – 6; 5) 33.
9. В случае, если точки 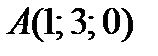 ,
, 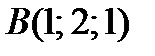 ,
, 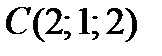 и
и 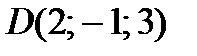 – вершины пирамиды, то угол между гранями ABC и ADC равен
– вершины пирамиды, то угол между гранями ABC и ADC равен
Варианты ответов:
1) 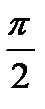 ; 2)
; 2) 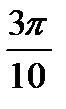 ; 3)
; 3) 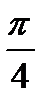 ; 4)
; 4) 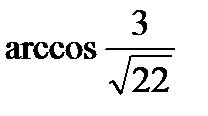 ; 5)
; 5) 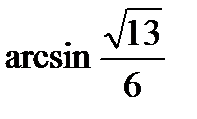 .
.
10. В случае, если точки 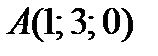 ,
, 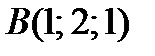 ,
, 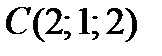 и
и 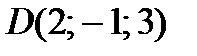 – вершины пирамиды, то прямая AD образует с гранью ABC угол, величина которого равна
– вершины пирамиды, то прямая AD образует с гранью ABC угол, величина которого равна
Варианты ответов:
1) 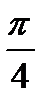 ; 2)
; 2) 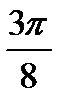 ; 3)
; 3) 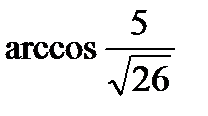 ; 4)
; 4) 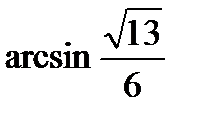 ; 5)
; 5) 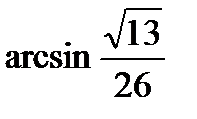 .
.
ФУНКЦИИ
6.2. Функция: определения и основные понятия
Функцией 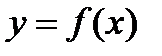 именуют такую зависимость переменной
именуют такую зависимость переменной 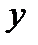 от переменной
от переменной 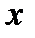 , при которой каждому допустимому значению
, при которой каждому допустимому значению 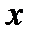 соответствует единственное значение
соответствует единственное значение 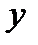 . Наряду с этим переменную х именуют свободной переменной либо доводом функции, а переменную у – зависимой от х переменной либо значением функции.
. Наряду с этим переменную х именуют свободной переменной либо доводом функции, а переменную у – зависимой от х переменной либо значением функции.
К примеру, равенства 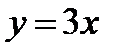 ,
, 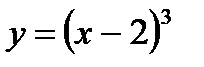 ,
, 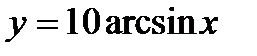 ,
, 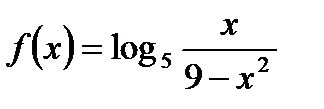 ,
, 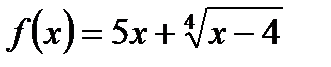 – функции.
– функции.
Уравнение 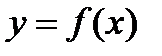 задает функцию очевидно, а уравнение
задает функцию очевидно, а уравнение 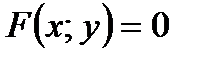 задает функцию неявно. Дабы задать функцию очевидно, нужно в уравнении
задает функцию неявно. Дабы задать функцию очевидно, нужно в уравнении 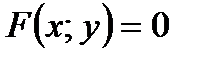 выразить одну переменную через другую.
выразить одну переменную через другую.
К примеру, зададим очевидно уравнение преувеличения 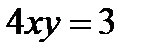 , выразив переменную y через переменную x:
, выразив переменную y через переменную x: 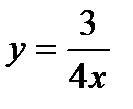
Но, не всякое равенство, содержащее переменные, есть функцией. К примеру, уравнение окружности 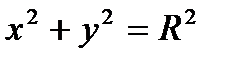 нельзя считать функцией, поскольку каждому значению х соответствует два значения у.
нельзя считать функцией, поскольку каждому значению х соответствует два значения у.
К примеру, в случае, если уравнение окружности имеет форму 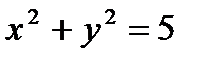 , то при
, то при 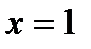 возьмём:
возьмём: 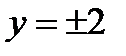 . Но в случае, если разглядывать не всю окружность, а лишь ее часть, то возможно конкретно записать у, как функцию от х. Так, к примеру, в случае, если забрать часть окружности, расположенную над осью абсцисс, то
. Но в случае, если разглядывать не всю окружность, а лишь ее часть, то возможно конкретно записать у, как функцию от х. Так, к примеру, в случае, если забрать часть окружности, расположенную над осью абсцисс, то 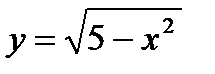 , а вдруг забрать часть окружности, расположенную под осью абсцисс, то
, а вдруг забрать часть окружности, расположенную под осью абсцисс, то 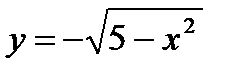 .
.
Множество всех допустимых значений переменной 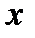 образуют область определения функции. Область определения функции обозначают
образуют область определения функции. Область определения функции обозначают 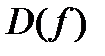 . Множество всех допустимых значений переменной
. Множество всех допустимых значений переменной 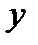 образуют область значений функции. Область значений функции обозначают
образуют область значений функции. Область значений функции обозначают 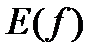 .
.
К примеру:
1) областью определения функции 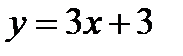 есть множество всех настоящих чисел и область значений данной функции – множество всех настоящих чисел;
есть множество всех настоящих чисел и область значений данной функции – множество всех настоящих чисел;
2) область определения функции 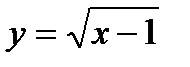 составляют числа, находящиеся в собствености промежутку
составляют числа, находящиеся в собствености промежутку 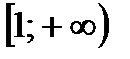 , а область ее значений – числа, находящиеся в собствености промежутку
, а область ее значений – числа, находящиеся в собствености промежутку 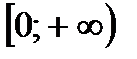 .
.
Графиком функции 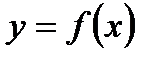 именуют множество точек плоскости, координаты которых удовлетворяют данной функциональной зависимости, другими словами точек вида
именуют множество точек плоскости, координаты которых удовлетворяют данной функциональной зависимости, другими словами точек вида 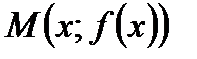 . График функции представляет собой некую линию на плоскости. Дабы выстроить график функции, возможно, придавая переменной х каждые допустимые значения, отыскать соответствующие им значения функции и нанести полученные точки на координатную плоскость. Соединив эти точки, возьмём график функции. Наряду с этим выстроенный так график не всегда верно отражает функциональную зависимость между переменными. Дабы выстроить графическое изображение верно, нужно знать вид функциональной зависимости и наносить на координатную плоскость характерные для данной зависимости точки. В случае, если функция сложная, то выполняют ее полное изучение.
. График функции представляет собой некую линию на плоскости. Дабы выстроить график функции, возможно, придавая переменной х каждые допустимые значения, отыскать соответствующие им значения функции и нанести полученные точки на координатную плоскость. Соединив эти точки, возьмём график функции. Наряду с этим выстроенный так график не всегда верно отражает функциональную зависимость между переменными. Дабы выстроить графическое изображение верно, нужно знать вид функциональной зависимости и наносить на координатную плоскость характерные для данной зависимости точки. В случае, если функция сложная, то выполняют ее полное изучение.
Функция 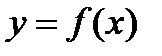 возрастает на промежутке (a; b), в случае, если для любых x1 и x2, принадлежащих промежутку (a; b), из неравенства
возрастает на промежутке (a; b), в случае, если для любых x1 и x2, принадлежащих промежутку (a; b), из неравенства 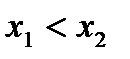 направляться неравенство
направляться неравенство 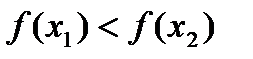 (рис. 6.1).
(рис. 6.1).
Функция 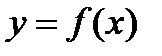 убывает на промежутке (a; b), в случае, если для любых x1 и x2, принадлежащих промежутку (a; b), из неравенства
убывает на промежутке (a; b), в случае, если для любых x1 и x2, принадлежащих промежутку (a; b), из неравенства 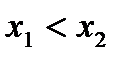 направляться неравенство
направляться неравенство 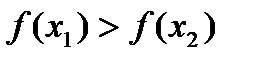 (рис. 6.2).
(рис. 6.2).
| b |
| y = f (x) |
| а |
| f (x2) |
| f (x1) |
| х2 |
| х1 |
| у |
| х |
| y = f (x) |
| f (x1) |
| f (x2) |
| х2 |
| а |
| х1 |
| у |
| х |
Функция есть монотонной, если она или лишь возрастает, или лишь убывает на 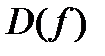 .
.
К примеру, функция, график которой изображен на рисунке 6.3, монотонна, поскольку она возрастает на множестве всех настоящих чисел, а функция, график которой изображен на рисунке 6.4, не монотонна, поскольку на промежутке 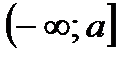 она убывает, а на промежутке
она убывает, а на промежутке 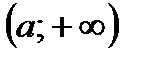 – возрастает.
– возрастает.
| y = f (x) |
| х |
| О |
| у |
| y = f (x) |
| х |
| О |
| у |
Говорят, что числовое множество симметрично относительно точки 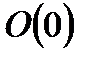 (начала отсчета) координатной прямой, если оно содержит лишь противоположные элементы.
(начала отсчета) координатной прямой, если оно содержит лишь противоположные элементы.
К примеру, числовые множества 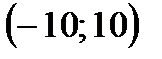 ,
, 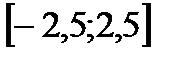 ,
, 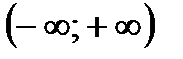 – симметричные, а множества
– симметричные, а множества 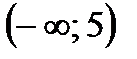 ,
, 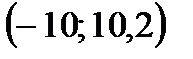 и
и 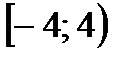 – не симметричные.
– не симметричные.
Функция есть четной, в случае, если: 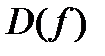 – симметричное множество относительно начала отсчета и
– симметричное множество относительно начала отсчета и 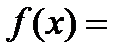
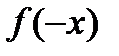 . График четной функции симметричен относительно оси
. График четной функции симметричен относительно оси 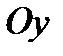 .
.
Функция есть нечетной, в случае, если: 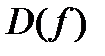 – симметричное множество относительно начала отсчета и
– симметричное множество относительно начала отсчета и 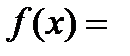
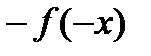 . График нечетной функции симметричен относительно точки
. График нечетной функции симметричен относительно точки 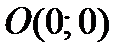 .
.
К примеру:
1) функция 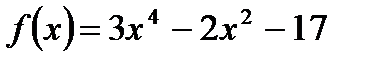 четная, поскольку:
четная, поскольку:
а) 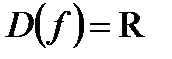 – симметричное множество относительно начала отсчета;
– симметричное множество относительно начала отсчета;
б) 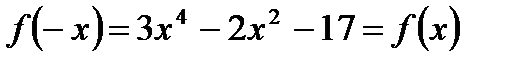 ;
;
2) функция 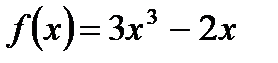 четная, поскольку:
четная, поскольку:
а) 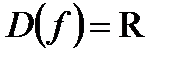 – симметричное множество относительно начала отсчета;
– симметричное множество относительно начала отсчета;
б) 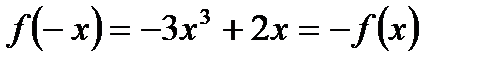 ;
;
3) функция 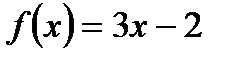 не есть четной и не есть нечетной, поскольку
не есть четной и не есть нечетной, поскольку 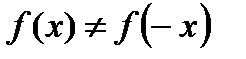 .
.
Функция 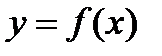 именуется периодической, в случае, если существует такое число
именуется периодической, в случае, если существует такое число 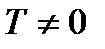 , при котором для всех х из области определения функции выполняется равенство
, при котором для всех х из области определения функции выполняется равенство 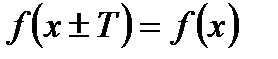 .
.
К примеру, тригонометрические функции 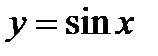 ,
, 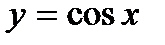 ,
, 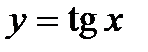 и
и 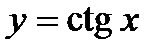 являются периодическими, поскольку выполняются равенства:
являются периодическими, поскольку выполняются равенства: 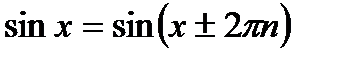 ,
, 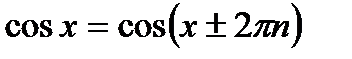 ,
, 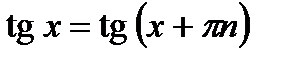 и
и 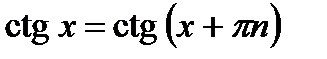 , где
, где 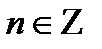 .
.
Дабы выстроить график периодической функции, достаточно выстроить ее график на главном (мельчайшем) периоде T и выполнить параллельный перенос этого графика на протяжении оси абсцисс на любое количество периодов влево и вправо.
К примеру, разглядим функцию 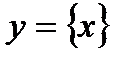 . Увидим, что запись
. Увидим, что запись 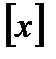 обозначает солиднейшую целую часть некоего числа, не превосходящую это число, а запись
обозначает солиднейшую целую часть некоего числа, не превосходящую это число, а запись 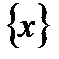 обозначает его дробную часть. Так, к примеру,
обозначает его дробную часть. Так, к примеру, 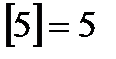 ,
, 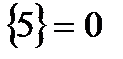 ,
, 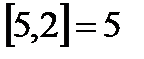 ,
, 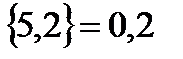 ,
, 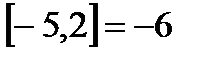 ,
, 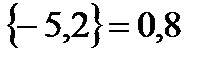 . Тогда функция
. Тогда функция 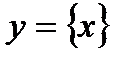 есть периодической с главным периодом, равным 1. На рисунке 6.5 выстроен график данной функции на ее главном периоде
есть периодической с главным периодом, равным 1. На рисунке 6.5 выстроен график данной функции на ее главном периоде 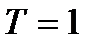 , а на рисунке 6.6 выстроен график данной функции на нескольких периодах.
, а на рисунке 6.6 выстроен график данной функции на нескольких периодах.
| х |
| О |
| у |
| х |
| О |
| у |
Точки пересечения графика функции с осью абсцисс именуют нулями функции.
Дабы отыскать нули функции 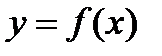 нужно решить уравнение
нужно решить уравнение 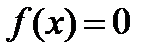 .
.
К примеру, отыщем нули функции 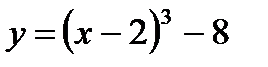 . Решая уравнение
. Решая уравнение 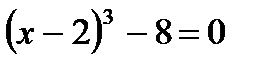 , возьмём
, возьмём 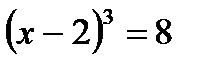 ,
, 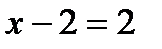 и
и 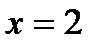 .
.
Функция 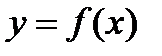 обратима, т. е. имеет обратную функцию
обратима, т. е. имеет обратную функцию 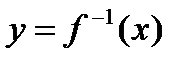 , если она либо монотонно возрастает либо монотонно убывает на всей собственной области определения.
, если она либо монотонно возрастает либо монотонно убывает на всей собственной области определения.
Функции 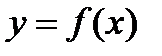 и
и 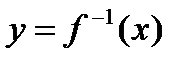 образуют несколько взаимно обратных функций. Взаимно обратные функции владеют следующими особенностями:
образуют несколько взаимно обратных функций. Взаимно обратные функции владеют следующими особенностями:
1) область определения функции 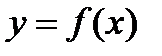 есть областью значений функции
есть областью значений функции 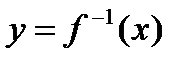 , а область значений функции
, а область значений функции 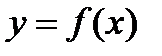 есть областью определения функции
есть областью определения функции 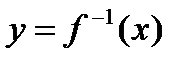 , т.е.
, т.е. 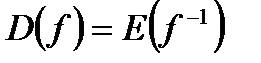 ,
, 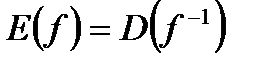 ;
;
2) в случае, если функция 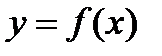 монотонно возрастает (убывает), то и функция
монотонно возрастает (убывает), то и функция 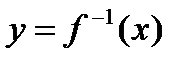 возрастает (убывает);
возрастает (убывает);
3) графики взаимно обратных функций симметричны относительно прямой 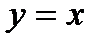 .
.
К примеру, функции 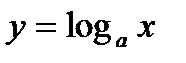 и
и 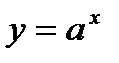 (рис. 6.7) взаимно обратные, поскольку формулы
(рис. 6.7) взаимно обратные, поскольку формулы 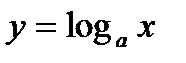 и
и 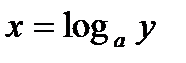 высказывают одну и ту же функциональную зависимость между переменными. Причем:
высказывают одну и ту же функциональную зависимость между переменными. Причем:
а) 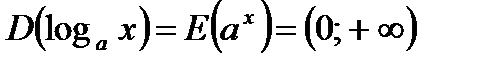 ,
, 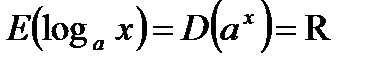 ;
;
б) обе функции монотонно возрастают на всей области их определения;
в) их графики симметричны относительно прямой 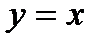 .
.
| y = x |
| y=ax |
| y=loga x |
| О |
| у |
| х |
Дабы отыскать функцию обратную функции 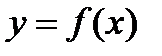 нужно решить уравнение довольно переменной х и в этом уравнении заменить х на у, а у заменить на х.
нужно решить уравнение довольно переменной х и в этом уравнении заменить х на у, а у заменить на х.
К примеру, отыщем функцию обратную функции 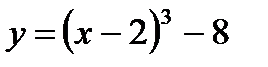 . Решим уравнение
. Решим уравнение 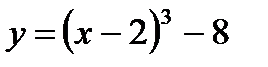 довольно х, другими словами, выразим переменную х очевидно. Возьмём:
довольно х, другими словами, выразим переменную х очевидно. Возьмём: 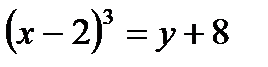 ,
, 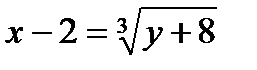 и
и 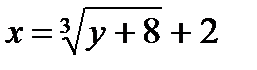 . Заменив в этом уравнении х на у, а у на х, запишем:
. Заменив в этом уравнении х на у, а у на х, запишем: 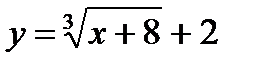 . Функции
. Функции 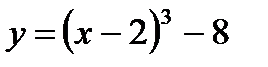 и
и 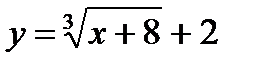 взаимно обратные.
взаимно обратные.
Разглядим две функции 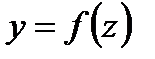 и
и 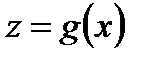 . Функцию вида
. Функцию вида 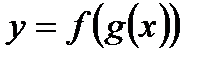 именуют сложной функцией.
именуют сложной функцией.
К примеру: 1) в случае, если 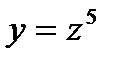 , а
, а 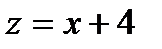 , то
, то 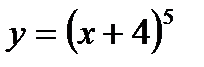 ;
;
2) в случае, если 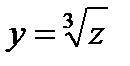 , а
, а 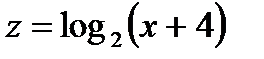 , то
, то 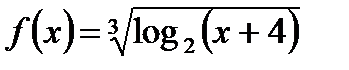 ;
;
3) в случае, если 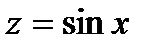 , а
, а 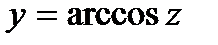 , то
, то 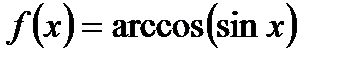 .
.
Асимптоты графика функции
Асимптотой линии именуют прямую, к которой неограниченно приближается эта линия, в то время, когда ее точка неограниченно удаляется от начала координат.
Виды асимптот:
1) вертикальные – параллельные оси Оу;
2) наклонные – пересекающие ось Оу;
3) горизонтальные – параллельные оси ОУ.
1. Уравнение вертикальной асимптоты графика функции 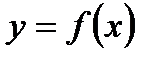 имеет форму
имеет форму 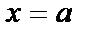 , при условии, что выполняется хотя бы одно из условий:
, при условии, что выполняется хотя бы одно из условий: 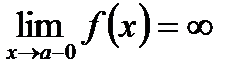 ,
, 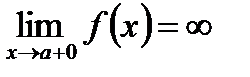 .
.
2. Уравнение наклонной асимптоты графика функции 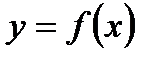 имеет форму
имеет форму 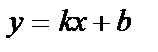 , где
, где
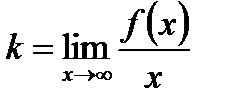 , (6.18)
, (6.18)
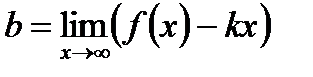 . (6.19)
. (6.19)
3. В случае, если 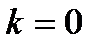 , то имеем горизонтальную асимптоту
, то имеем горизонтальную асимптоту 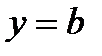 .
.