2.4.1. Аналитическое определение положения полностью жёсткого тела. Углы Эйлера
Продемонстрируем, как возможно задать шесть свободных параметров, конкретно определяющих положение полностью жёсткого тела. Пускай – неподвижная прямоугольная совокупность координат и пускай жёсткое тело неизменно связано с некоей второй подвижной, прямоугольной совокупностью O??? (рис. 2.35).
Координаты начала О подвижной совокупности довольно неподвижной следующие:
В общем случае, в то время, когда начала обеих совокупностей координат разны, возможно выяснить положение жёсткого тела тремя числами a, b, c и углами Эйлера ?, ?, ?, определяющими положение подвижной совокупности O??? довольно третьей промежуточной совокупности координат , начало которой сходится с началом подвижной совокупности, а оси параллельны осям неподвижной.
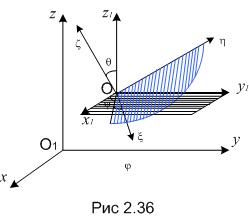В случае, если прямая ОК имеется прямая пересечения O?? и , именуемая линией узлов, то углы эти следующие (рис. 2.36):
1) угол ? между O? и ОК;
2) угол ? между ОК и ;
3) угол ? между O? и .
Рис.2.36
Все углы берутся между хорошими направлениями осей. Хорошее направление линии узлов ОК выбирается так, дабы наблюдатель, наблюдающий на протяжении КО, видел поворот к O?, против хода часовой стрелки.
По аналогии с терминами, принятыми в астрономии, эти углы время от времени именуют:
- ? – углом собственного вращения тела;
- ? – углом прецессии;
- ? – углом нутации.
Перемещение свободного жёсткого тела определяется шестью уравнениями, именуемыми уравнениями перемещения свободного жёсткого тела:
(2.71)
Вид первых трех уравнений, определяющих поступательную часть перемещения жёсткого тела, зависит от выбора полюса, поскольку координаты разных точек тела разны. Вид остальных трех уравнений от выбора полюса не зависит.
2.4.2. Понятие мгновенного перемещения
Кинематическое состояние любого материального тела в разглядываемый момент времени определяется размещением в пространстве его точек и их скоростям сейчас. Перемещение тела мы воображаем как постоянный и последовательный переход его из одного кинематического состояния в второе. Наровне с определением положения точек движущегося тела, появляется вопрос о распределении скоростей точек тела в разглядываемый момент времени.
Под мгновенным перемещением тела будем осознавать только распределение скоростей точек движущегося тела сейчас времени. Что касается ускорений точек и траекторий тела этих точек, то они смогут быть какими угодно.
Допустим, что распределение скоростей точек жёсткого тела сейчас времени определяется формулой
где – некая точка тела; – некий вектор, отложенный от данной точки (рис. 2.37). В этом случае будем говорить о мгновенном вращательном перемещении тела около мгновенной оси вращения с вектором мгновенной угловой скорости, равным .
Мгновенная ось вращения проходит через точку и определяется линией действия вектора .
2.4.3. Теорема Эйлера
Установим закон распределения скоростей точек тела в разглядываемый момент времени (мгновенных скоростей) в общем случае перемещения свободного жёсткого тела.
Для любого перемещения жёсткого тела честна теорема:
Всякое мгновенное перемещение жёсткого тела возможно представить как следствие сложения мгновенного поступательного перемещения со скоростью произвольно выбранной точки тела и мгновенного вращательного перемещения около мгновенной оси вращения, проходящей через эту точку.
Для доказательства выберем в пространстве неподвижную совокупность координат Oxyz (рис. 2.38). Перемещение жёсткого тела возможно выяснить, введя совокупность координат , жестко связанную с телом. Тогда положение жёсткого тела определится положением системы и положением полюса координат довольно Oxyz;
– орты осей координат.
Из рис. 2.38 для точки М имеем
где .
Вектор скорости точки М определим, дифференцируя выражение (2.72) по времени:
Второе слагаемое в равенстве (2.73) определим с учетом того, что вектор , соединяющий две точки жёсткого тела, постоянный по величине
где – вектор угловой скорости вращения жёсткого тела около мгновенной оси вращения, проходящей через точку .
С учетом выражения (2.74) возьмём формулу для вектора скорости любой точки М жёсткого тела:
Векторы и не зависят от выбора точки М. Второе слагаемое в формуле (2.75) имеется та скорость, которую имела бы точка М, если бы тело вращалось около некоей неподвижной оси, проходящей через точку , с вектором угловой скорости, равным .
Так, перемещение жёсткого тела возможно разглядывать как сложение двух перемещений: для того чтобы, в котором все точки тела имеют сейчас одну и ту же скорость (что соответствует мгновенному поступательному перемещению) и другого – мгновенного вращения около некоей оси, проходящей через точку с угловой скоростью .
В следующий момент времени все векторы, входящие в правую часть формулы (2.75), изменяются. Никаких вторых мгновенных перемещений жёсткое тело, как это направляться из приведенного доказательства, не имеет.
Теорема Эйлера доказана.
Доказано, что вектор мгновенной угловой скорости тела не зависит от выбора полюса .
Тема 2.5. Перемещение жёсткого тела, имеющего
одну неподвижную точку
Разглядим перемещение жёсткого тела, одна из точек которого во все время перемещения остается неподвижной. При таком перемещении все остальные точки тела движутся по сферическим поверхностям, центры которых совпадают с неподвижной точкой. Такое перемещение именуют сферическим.
2.5.1. Уравнение сферического перемещения жёсткого тела. Мгновенная ось вращения и мгновенная угловая скорость
Для определения положения тела в любой момент времени воспользуемся двумя совокупностями осей координат: неподвижной совокупностью Oxyz с началом в неподвижной точке О и подвижной совокупностью O???, неизменно связанной с жёстким телом, с началом в той же неподвижной точке О (рис. 2.39).
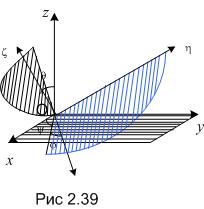Положение тела конкретно определяется тремя углами Эйлера – ?, ?, ?. При перемещении жёсткого тела, одна из точек которого остается неподвижной, углы ?, ?, ? непрерывно изменяются во времени, являясь функциями времени t:
Эти уравнения – уравнения сферического перемещения жёсткого тела. Рис.2.39
Для разглядываемого перемещения теорема Эйлера возможно сформулирована так:
Всякое мгновенное перемещение жёсткого тела, имеющего одну неподвижную точку, есть мгновенным вращательным перемещением около мгновенной оси вращения, проходящей через эту точку.
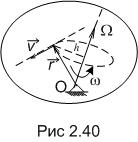
В отличие от вращения жёсткого тела около неподвижной оси, у вектора мгновенной угловой скорости с течением времени изменяется не только модуль, но и линия действия. Вектор откладывается от неподвижной точки О по мгновенной оси в такую сторону, дабы, смотря навстречу
этому вектору, видеть вращение тела, Рис.2.40
происходящее против перемещения часовой стрелки (рис. 2.40). Мгновенная ось представляет собой геометрическое место точек тела, скорость которых сейчас равна нулю.
2.5.2. Угловое ускорение тела при сферическом
перемещении
При сферическом перемещении тела положение мгновенной оси вращения со временем изменяется, и, следовательно, изменяется не только модуль, но и направление вектора угловой скорости тела.
Пускай моменту времени t соответствует вектор угловой скорости , а моменту времени вектор (рис. 2.41), ? — приращение вектора за время .
Вектор среднего углового ускорения определяется по формуле
Направление сходится с направлением . Предел этого отношения при именуется угловым ускорением тела в момент времени t:
В случае, если мы будем откладывать вектор от неподвижной точки О, то финиш его обрисует кривую либо годограф скорости (рис. 2.42).
Определим скорость перемещения точки А – финиша вектора угловой скорости – по годографу в момент времени t. Радиус-вектор данной точки есть вектор , а скорость точки равна
Так как векторы и равны одной и той же величине, то они равны между собой:
(2.77)
т.е. угловое ускорение тела геометрически равняется линейной скорости финиша вектора угловой скорости. Вектор откладывается от неподвижной точки.
Прямая, по которой направлен вектор углового ускорения, именуется осью углового ускорения и обозначается Е.
2.5.3. Скорости точек тела при сферическом перемещении. Формулы Эйлера
На основании теоремы Эйлера вектор скорости любой точки М жёсткого тела, имеющего одну неподвижную точку, равен
где , а – вектор мгновенной угловой скорости тела (рис. 2.43).
В случае, если мы обозначим через проекции вектора на подвижные координаты оси Oxyz, а через x, y, z – координаты точки М в данной же совокупности координат, то возьмём
где – орты осей координат Oxyz. Тогда
Проекции вектора на неподвижные оси координат будут иметь вид
В правых частях формул изменяются и координаты и проекции точки М. Дабы избежать последнего события, проектируют векторное равенство (2.78) на подвижные оси координат O???, скрепленные с телом. Подобно приобретаем:
В правых частях последних формул с течением времени изменяются лишь проекции векторов , а координаты точки М в подвижной совокупности координат, жестоко связанной с телом, остаются неизменными. Формулы (2.79) и (2.80) установлены Эйлером.
Модуль скорости любой точки тела имеет форму
(2.81)
Иначе, потому, что скорость любой точки тела определяется как вращательная около мгновенной оси, то модуль определяется по формуле
где – протяженность перпендикуляра, опущенного из точки М на мгновенную ось вращения (рис. 2.44).
2.5.4. Ускорение точек жёсткого тела при сферическом перемещении. Теорема Ривальса
Для вычисления ускорения какой-либо точки тела при сферическом перемещении воспользуемся векторным выражением скорости данной же точки:
Ускорение точки определяется по формуле
Учтем, что
Тогда равенство (2.82) принимает вид
где — вращательное ускорение точки; – осестремительное ускорение точки.
Так,
Равенство (2.40) высказывает теорему Ривальса об ускорении точки тела, совершающего сферическое перемещение.
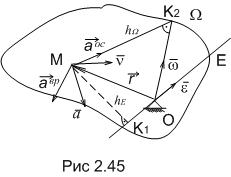Ускорение любой точки жёсткого тела при сферическом перемещении определяется как геометрическая сумма ее вращательного и осестремительного ускорения (рис. 2.45).
Модуль вращательного ускорения определяется следующим образом: Рис.2.45
(2.84)
где – малейшее расстояние от точки М до оси углового ускорения Е.
Направление определяется по правилу векторного произведения.
Вектор осестремительного ускорения направлен перпендикулярно векторам , т.е. по перпендикуляру, опущенному из точки М на мгновенную ось ?.
Модуль осестремительного ускорения определяется по формуле
(2.85)
где – малейшее расстояние от точки М до мгновенной оси вращения ?.
Модуль ускорения точки как диагональ параллелограмма ускорений возможно выяснить по формуле
(2.86)
2.5.5. Теорема об ускорении точек свободного
жёсткого тела
Ускорение точки свободного жёсткого тела равняется геометрической сумме ускорения полюса, осестремительного ускорения точки и ее вращательного ускорения, определенных довольно мгновенных оси и оси вращения углового ускорения, проходящих через полюс.
Скорость произвольной точки М свободного тела (рис. 2.46) равна
Ускорение точки
где
– ускорение полюса O; – вращательное ускорение точки М относительно оси углового ускорения Е, проходящей через полюс О; – осестремительное ускорение точки М довольно мгновенной оси вращения ?, проходящей через полюс О. Исходя из этого
. (2.88)
Тема 2.6. Сложное перемещение точки
Сложное перемещение точки – это такое перемещение, при котором точка (тело) в один момент участвует в двух либо нескольких перемещениях.
Примером сложного перемещения могут служить: перемещение пассажира, перемещающегося в вагоне движущегося поезда; перемещение человека, перемещающегося по лестнице движущегося эскалатора.
2.6.1. Относительное, переносное и полное
перемещение точки
Разглядим движущееся тело А (рис. 2.47) и точку М, не принадлежащую этому телу, а совершающую по отношению к нему некое перемещение.
Через произвольную точку О движущегося тела совершим неизменно связанные с этим телом оси Ox, Oy, Oz. Совокупность осей Oxyz именуют подвижной совокупностью отсчета. Неподвижной совокупностью отсчета именуют совокупность осей O1x1y1z1, связанную с некоторым условно неподвижным телом, в большинстве случаев с Почвой.
Перемещение точки М по отношению к неподвижной совокупности отсчета именуют безотносительным перемещением точки.
ускорение и Скорость точки в полном перемещении именуют полной абсолютным ускорением и скоростью точки и обозначают и .
Перемещение точки М по отношению к подвижной совокупности отсчета именуют относительным перемещением точки.
ускорение и Скорость точки в относительном перемещении именуют относительной относительным ускорением и скоростью точки и обозначают и .
Перемещение подвижной совокупности отсчета Oxyz и связанного с ней тела А по отношению к неподвижной совокупности отсчета O1x1y1z1 есть для точки М переносным перемещением.
ускорение и Скорость точки тела А, связанного с подвижной совокупностью отсчета, совпадающей сейчас с движущейся точкой М, именуют переносной переносным ускорением и скоростью точки М и обозначают и . К примеру, в случае, если человек идет на протяжении радиуса вращающейся платформы (рис. 2.48), то с платформой возможно связать подвижную совокупность отсчета, а с Почвой – неподвижную. Тогда перемещение платформы будет переносным, перемещение человека относительно платформы – относительным, а перемещение человека относительно Земли – безотносительным перемещением.
Переносной переносным ускорением и скоростью человека есть ускорение и скорость той точки платформы, где находится сейчас человек.
Перемещение точки М (см. рис. 2.48) по отношению к неподвижной совокупности отсчета, которое названо безотносительным перемещением, есть сложным, складывающимся из относительного и переносного перемещения точки.
Главная задача изучения сложного перемещения пребывает в установлении зависимости между ускорениями и скоростями относительного, переносного и безотносительного перемещений точки.
Положение точки М довольно неподвижной совокупности отсчета определяется радиус-вектором . Положение точки М довольно подвижной совокупности отсчета определяется радиус-вектором либо тремя координатами x, y, z:
Изменение радиус-вектора характеризует относительное перемещение точки М. Так, уравнения относительного перемещения точки имеют вид
(2.89)
2.6.2. Полная и относительная производные от вектора. Формула Бура
При рассмотрении сложного перемещения точки в общем случае переносного перемещения определяют трансформации векторных размеров с течением времени по отношению к совокупностям отсчета, движущимся относительно друг друга.
Введем обозначение производных от векторных размеров при рассмотрении их трансформации довольно разных совокупностей отсчета. Для любого вектора его производную по времени по отношению к неподвижной совокупности отсчета именуют полной (либо полной) производной и обозначают . Производную по времени при учете трансформации вектора довольно подвижной совокупности отсчета именуют относительной либо локальной производной и обозначают либо .
Установим зависимость между полной и относительной производными по времени векторов и размерами, характеризующими перемещение подвижной совокупности отсчета довольно неподвижной. Для этого разложим вектор на составляющие, параллельные осям подвижной совокупности координат (рис. 2.49):
Изменение вектора довольно неподвижной совокупности отсчета O1x1y1z1 в зависимости от времени складывается из трансформаций его проекций , , и единичных векторов , , подвижных осей благодаря перемещения подвижной совокупности координат довольно неподвижной. Вычислим полную производную:
Первые три слагаемые выражения (2.91) учитывают изменение вектора при неизменных , , и исходя из этого составляют относительную производную
Производные по времени единичных векторов определим по формулам Пуассона:
так как эти векторы не изменяются от поступательного перемещения со скоростью вместе с подвижной совокупностью отсчета. Вектор – угловая скорость вращения подвижной совокупности отсчета около мгновенной оси вращения, проходящей через точку О. Подставляя значения производных единичных векторов в выражение (2.91), возьмём
либо, учитывая выражение (2.41),
Формула (2.92) – это формула Бура зависимости производных вектора в двух совокупностях отсчета, движущихся относительно друг друга. Из данной формулы направляться, что поступательная часть перемещения вместе с полюсом не воздействует на зависимость между производными, а воздействует лишь вращательная часть перемещения.
2.6.3. Теорема о сложении скоростей
Перемещение подвижной совокупности осей координат довольно неподвижной возможно охарактеризовать скоростью ее поступательного перемещения вместе с точкой О и вектором угловой скорости ее вращения около мгновенной оси вращения, проходящей через точку О (рис. 2.50).