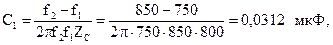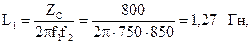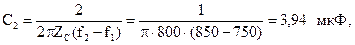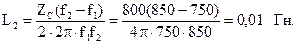К вторичным параметрам четырехполюсника относятся характеристические постоянная передачи и сопротивления.
Для каждого пассивного четырехполюсника существуют два таких характеристических сопротивления Z1C, Z2C (со стороны входных и выходных зажимов соответственно), каковые удовлетворяют следующим условиям: в случае, если сопротивление нагрузки ZH2 на выходе четырехполюсника равняется характеристическому Z2C, то входное сопротивление со стороны первичных зажимов равняется характеристическому Z1C; в случае, если при обратном включении четырехполюсника сопротивление нагрузки ZH1 равняется характеристическому Z1C, то входное сопротивление со стороны вторичных зажимов будет равняется характеристическому сопротивлению Z2C.
Такая нагрузка четырехполюсника именуется согласованной. При согласованной нагрузке утраты в четырехполюснике минимальны.
Характеристические сопротивления возможно вычислить как по известным коэффициентам четырехполюсника, так и по умелым данным, взятым при проведении опытов короткого замыкания и холостого хода:
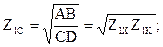
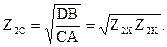
При согласованной нагрузке: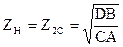 
.
Выходной напряжение и ток связаны зависимостью:
.
Тогда ток и напряжение на входе четырехполюсника:
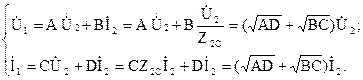
Комплексное число полагают равным еg,
где – постоянная передачи.
Входные и выходные напряжения и токи при согласованной нагрузке связаны соотношением:
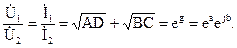
Либо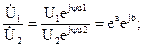 
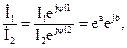
откуда: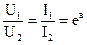 
, другими словами модуль входного напряжения в еа раз отличается от модуля выходного напряжения, а модуль входного тока в еа раз отличается от модуля выходного тока;
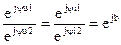, другими словами входное напряжение опережает выходное напряжение на угол b и начальные фазы входного и выходного токов отличаются на такой же угол.
Величина а именуется коэффициентом затухания. Единицами измерения коэффициента затухания являются неперы (Нп) и белы (Б).
Затухание в неперах: аНп=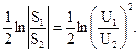 
В случае, если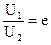 
, то затухание равняется 1 Нп.
Затухание в белах: аБ=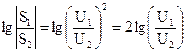 
, а в децибелах: адБ= 
.
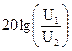Величина b именуется коэффициентом фазы и измеряется в градусах либо в радианах.
Энергопередача от источника через пассивный четырехполюсник к приемнику характеризуется коэффициентом нужного действия четырехполюсника и утратами мощности в нем. КПД определяется как отношение мощности нагрузки P2=U2I2 cos 2 к входной мощности P1=U1I1 cos 1, а утраты мощности как разность этих мощностей Р = Р1-Р2.
Электрические фильтры
Электрические фильтры – это четырехполюсники, включаемые между источником питания (генератором) и приемником (нагрузкой), назначение которых пребывает в том, дабы без затухания пропускать к приемнику токи одних частот и задерживать либо пропускать, но с громадным затуханием, токи вторых частот (рис. 5.4).
 |
Рис. 5.4
Диапазон частот, пропускаемый фильтром без затухания, именуется полосой прозрачности (ПП). В совершенном случае нужно обеспечить нулевое затухание сигнала (коэффициент затухания = 0) в этом диапазоне. Диапазон частот, пропускаемый с затуханием именуется полосой затухания (ПЗ).
Электрические фильтры делают в большинстве случаев из L и С элементов. В базе их работы лежит зависимость реактивных сопротивлений от частоты:
Подключение резисторов с сопротивлением R ведет к подавлению сигналов всех частот, исходя из этого в пассивных электрических фильтрах они не используются.
Делают фильтры по симметричной Т- либо П- образной схеме четырехполюсника, ( либо ), согласованного по нагрузке (ZH=ZC). Сопротивления Z1 и Z4 именуют продольными, а Z3 и Z5 – поперечными.
Электрические фильтры, в которых произведение продольного сопротивления на соответствующее поперечное, представляет собой некое постоянное для данного фильтра число k, независящее от частоты, принято именовать k-фильтрами. Фильтры, у которых это произведение зависит от частоты, именуют m-фильтрами.
 |
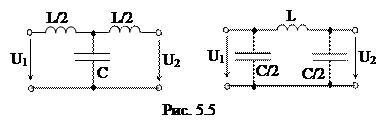Фильтры нижних частот (ФНЧ) пропускают сигналы в диапазоне частот от ?1 = 0 до ?2. На рис. 5.4 изображены несложные П- и Т-образные схемы фильтров низкой частоты.
В этих схемах и . Индуктивные продольные сопротивления с возрастанием частоты возрастают и гасят высшие гармоники; поперечные емкостные проводимости с повышением частоты так же возрастают и токи высших гармоник через поперечные ветви возвращаются на вход четырехполюсника.
Граничные частоты для полосы пропускания определяют из условия:
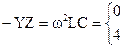откуда и .
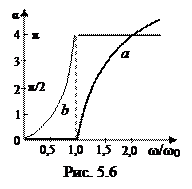На рис. 5.6 продемонстрированы зависимости коэффициента затухания a и коэффициента фазы b в зависимости от .
Фильтры верхних частот (ФВЧ) пропускают сигналы в диапазоне частот от ?1 до ?2= ?. На рис. 5.7 изображены несложные П- и Т-образные схемы фильтров, пропускающих сигналы верхних и задерживающие сигналы нижних частот.
 |
В этих схемах и . Продольные емкостные сопротивления при низких частотах имеют громадные сопротивления и гасят токи низших гармоник, а при повышении частоты емкостное сопротивление значительно уменьшается, и высшие гармоники с маленьким затуханием передаются на выход. Продольная индуктивная проводимость имеет громадное значение на низких частотах, и токи этих частот через поперечные ветви возвращаются на вход фильтра. На громадных частотах проводимость поперечных ветвей значительно уменьшается, и токи высших частот по пути мельчайшего сопротивления поступают на выход фильтра.
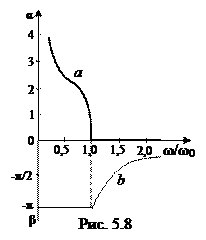Граничные частоты для полосы пропускания определяют из условия:
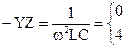откуда
и .
На рис. 5.8 продемонстрированы зависимости коэффициента затухания a и коэффициента фазы b в зависимости от .
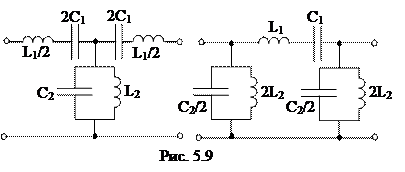
Полосовые фильтры (ПФ) пропускают сигналы в диапазоне частот от ?1 до ?2 и подавляют сигналы остальных частот. Полосовой фильтр возможно взять, в случае, если совместить электрически между собой схемы фильтров низкой частоты (рис. 5.5) с полосой пропускания ?Н1 = 0 до ?Н2 и высокой частоты (рис. 5.7) с полосой пропускания ?В1 до ?В2 =?. Тогда полученный фильтр будет пропускать сигналы в диапазоне частот от ?В1 до ?Н2, как продемонстрировано на частотной чёрте рис. 5.10. На рис. 5.9 приведены две схемы полосовых фильтров, имеющие Т- и П-образные формы.
Дабы при одной и той же частоте стали равны нулю продольные сопротивления Z (резонанс напряжений) и поперечные проводимости Y (резонанс токов), нужно выполнить условие, определяющее частоту:
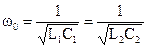при котором .
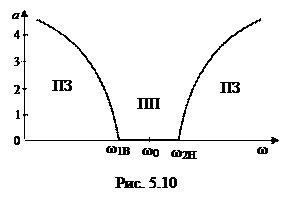
Заграждающие фильтры (ЗФ) пропускают сигналы в диапазоне частот от 0 до ?1 и от ?2 до ?, сигналы в диапазоне частот от ?1 до ?2 подавляются. Заграждающий фильтр возможно взять в случае, если, в случае, если совместить электрически между собой схемы фильтров низкой частоты с полосой пропускания ?Н1 = 0 до ?Н2 и высокой частоты с полосой пропускания ?В1 до ?В2 = ?. Тогда полученный фильтр будет подавлять сигналы в диапазоне частот от ?Н2 до ?В1, как продемонстрировано на частотной чёрте рис. 5.11.
Тогда при частоте ?0 возможно взять разрыв продольных сопротивлений Z и замыкание поперечных проводимостей Y. Для этого нужно выполнить условия:
и .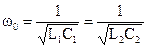
На рис. 5.12 приведены две схемы заграждающих фильтров, имеющие Т- и П-образные формы.
 |
Примеры ответа задач
5.2.1 Четырехполюсник, схема соединения элементов которого приведена на рис. 5.13, имеет параметры R=XL=10 Ом, ХС=20 Ом.
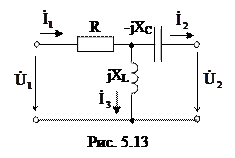Выяснить коэффициенты А-формы записи уравнений четырехполюсника и убедиться, что результаты удовлетворяют соотношению AD-BC=1.
Расчет коэффициентов выполнить посредством законов Кирхгофа и по входным сопротивлениям в режиме короткого замыкания и холостого хода.
Уравнения четырехполюсника в А-форме имеют вид:
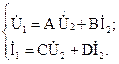
1) Составим уравнения по законам Кирхгофа для разглядываемой схемы.
В соответствии с первому закону Кирхгофа: .
По второму закону Кирхгофа составим уравнения для внешнего и правого контуров схемы:
;
.
Из второго уравнения выразим ток:
,
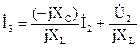и подставим полученное выражение в уравнение, составленное по первому закону Кирхгофа:
.
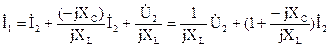Сравнив полученное выражение с уравнением четырехполюсника, составленным для тока, возможно выяснить коэффициенты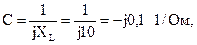 
и
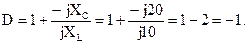
Для определения коэффициентов А и В подставим выражение, полученное для тока в уравнение, составленное по второму закону Кирхгофа для внешнего контура:
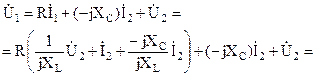
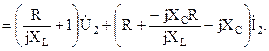
Сравнив полученное выражение с уравнением четырехполюсника, составленным относительно напряжения, отыщем коэффициенты:
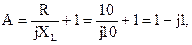
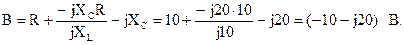
Удостоверимся в надежности исполнение соотношения между коэффициентами А-формы записи уравнений четырехполюсника:
AD – BC = (1 – j1)(–1) – (–10 – j20)(–j0,1) = –1 + j1 – j1+ 2 = 1,
что и требовалось доказать.
2) Вычислим коэффициенты по входным сопротивлениям в режиме короткого замыкания и холостого хода.
Вычислим входные сопротивления в режимах короткого замыкания и холостого хода при прямом включении четырехполюсника (рис.2.14, а, б):
,
 |
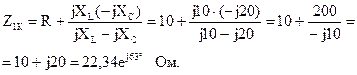
Вычислим входные сопротивления в режимах короткого замыкания и холостого хода при обратном включении четырехполюсника (рис. 5.15, а, б):
 |
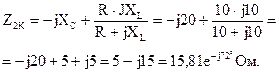
По известным формулам вычислим значения коэффициентов:
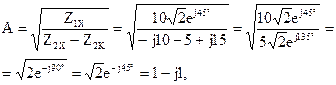
B=A Z2K=(1-j1)·(5-j15)=5-j5-j15-15= (-10-j20) Ом;
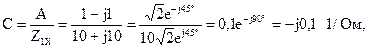
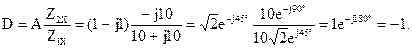
Результаты расчетов соответствуют значениям коэффициентов, взятым посредством законов Кирхгофа.
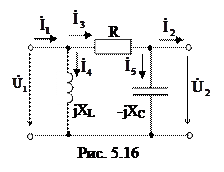5.2.2Четырехполюсник, схема которого приведена на рис. 5.16, имеет параметры:
R = XL = 10 Ом, ХС = 20 Ом. Выяснить коэффициенты А-формы записи уравнений четырехполюсника и убедиться, что результаты удовлетворяют соотношению AD – BC = 1.
Расчет коэффициентов выполнить посредством законов Кирхгофа и по входным сопротивлениям в режиме короткого замыкания и холостого хода.
Уравнения четырехполюсника в А-форме имеют вид:
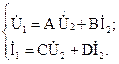
1) Составим уравнения по законам Кирхгофа для разглядываемой схемы.
По первому закону Кирхгофа составим два уравнения
и
По второму закону Кирхгофа составим уравнение для внешнего контура схемы:
Так как напряжение на зажимах четвертой ветви рано входному напряжению четырехполюсника, а напряжение на пятой ветви равняется – выходному, то по закону Ома возможно выразить токи в ветвях:
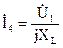и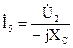 
.
Выразим значение тока третьей ветви через выходные режимные параметры четырехполюсника, подставив выражение для тока в уравнение, составленное по первому закону Кирхгофа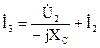 
. Полученное выражение подставим в уравнение, составленное по второму закону Кирхгофа:
.
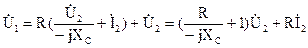Сравнив полученное выражение с уравнением четырехполюсника, составленным относительно напряжения, отыщем коэффициенты:
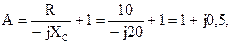
Возможно записать, подставив одно в второе уравнения, составленные по первому закону Кирхгофа .
Подставим в полученное уравнение значения токов четвертой и пятой ветвей и уже известное выражение для входного напряжения:
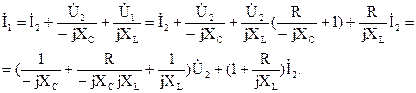
Сравнив полученное выражение с уравнением четырехполюсника, составленным довольно входного тока, отыщем коэффициенты:
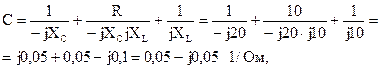
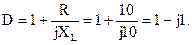
Удостоверимся в надежности исполнение соотношения между коэффициентами А-формы записи уравнений четырехполюсника:
AD-BC=(1+j0,5)·(1-j1)-10·(0,05-j0,05)=1-j1+j0,5+0,5-0,5+j0,5=1.
2) Вычислим коэффициенты по входным сопротивлениям в режиме короткого замыкания и холостого хода.
 |
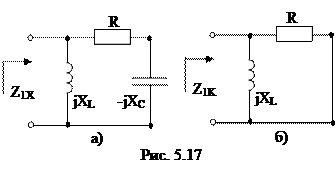Вычислим входные сопротивления в режимах короткого замыкания и холостого хода при прямом включении четырехполюсника (рис. 5.17, а и б).
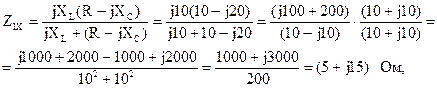
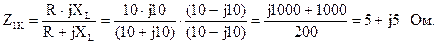
Вычислим входные сопротивления в режимах короткого замыкания и холостого хода при обратном включении четырехполюсника (рис. 5.18, а и б).
 |
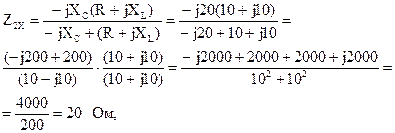
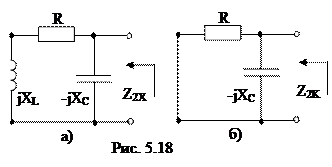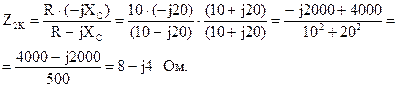
По известным формулам вычислим значения коэффициентов уравнений А-формы записи:
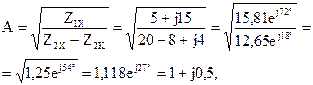
B = A Z2K = (1 + j0,5)·(8 – j4) = 8 + j4 – j4 + 2 = 10 Ом;
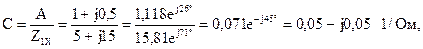
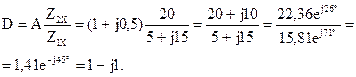
Результаты расчетов соответствуют значениям коэффициентов, взятым посредством законов Кирхгофа.
5.2.3 Несимметричный четырехполюсник имеет параметры А = 1; В = 2,83еj45° Ом; С = j0,5 См; D = j1. Отыскать характеристические постоянную передачи и сопротивления четырехполюсника.
Отыщем характеристические сопротивления:
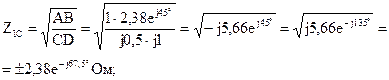
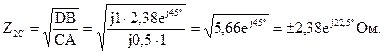
Отрицательные значения комплексного сопротивления не имеют физического смысла, поскольку они не реализуемы.
Определим постоянную передачи:
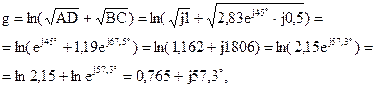
где коэффициент затухания , а коэффициент фазы либо
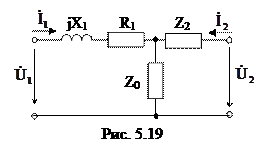5.2.4 Для четырехполюсника, эквивалентная схема которого приведена на рис. 5.19, составить уравнения, высказывающие зависимость комплексных напряжения входной ветви и тока выходной ветви от комплексных тока входной ветви и напряжения выходной ветви.
Параметры элементов цепи: Z0=12 Ом, Z2=6 Ом, Z1=(4+j3) Ом.
Искомую зависимость высказывают уравнения четырехполюсника Н-типа:
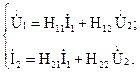
Коэффициенты Н11, Н12, Н21 и Н22 возможно выяснить на базе рассмотрения исходной схемы сперва при разомкнутых первичных зажимах, а после этого при короткозамкнутых вторичных полюсах с одновременным анализом уравнений Н-формы записи, соответствующим этим состояниям.
При разомкнутых первичных зажимах = 0 и совокупность уравнений примет вид:
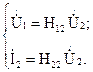откуда запишем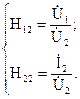 
Для разглядываемого режима:
, ,
и тогда возможно выяснить коэффициенты:
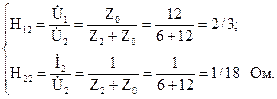
При короткозамкнутых вторичных полюсах =0 совокупность уравнений примет вид:
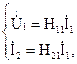откуда запишем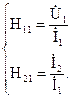 
Для разглядываемого режима:
, 
.
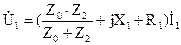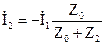Тогда возможно выяснить коэффициенты:
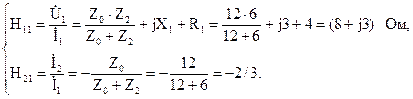
5.2.5 Выразить Z параметры обоюдного четырехполюсника через сопротивления его Т-схемы замещения (рис. 5.20).
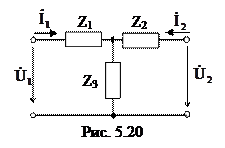Совокупность уравнений четырехполюсника в Z-форме записи имеет форму:
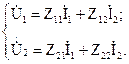
Запишем уравнения по законам Кирхгофа, связывающие напряжения четырехполюсника с входным и выходным токами, в один момент проводя анализ уравнений z-формы:
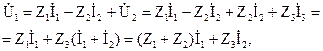
где – ток в поперечной ветви;
Сравнив выражение, полученное для входного напряжения четырехполюсника с первым уравнением Z- формы, возможно выяснить коэффициенты:
Довольно выходного напряжения запишем:
Сравнив полученное уравнение со вторым уравнением совокупности уравнений в z-форме, определим коэффициенты:
Из взятых значений видно, что для обоюдного четырехполюсника равны коэффициенты
5.2.6 При питании четырехполюсника со стороны первичных зажимов были измерены U1, I1, P1 в двух режимах:
а) холостого хода U1X = 100 B; I1X = 1 A; P1X = 0; б) в режиме замыкания U1К = 100 B; I1К = 1,41 A; P1К = 100 Вт. И в том и другом случае темперамент сопротивлений емкостный.
При обратном включении четырехполюсника при закороченных первичных зажимах были измерены U2К = 100 B; I2К = 1 A; P2К = 100 Вт. Как мы знаем, что Z1K/Z2K = Z1X/Z2X. Вычислить сопротивления прямого, обратного короткого замыкания и холостого хода. Выяснить по ним Z-параметры четырехполюсника.
При прямом включении четырехполюсника входные сопротивления для режимов короткого замыкания и холостого хода по показаниям измерительных устройств определяются:
,
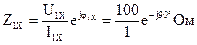где так как, в соответствии с исходным данным, нагрузка носит чисто емкостный темперамент (Р1Х=0);
,
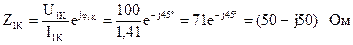где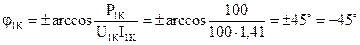 
,
так как как мы знаем, что темперамент сопротивлений емкостный.
,
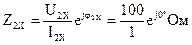где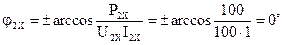 
.
Сопротивление Z2K отыщем из соотношения Z1K/Z2K = Z1X/Z2X:
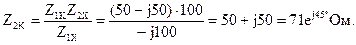
Уравнения четырехполюсника в Z-форме записи имеют вид:
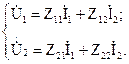
Для режима холостого хода при прямом = 0 и обратном = 0 включении четырехполюсника запишем:
тогда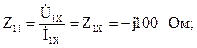 
тогда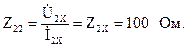 
Для режима замыкания на вторичных зажимах четырехполюсника ( ) запишем:
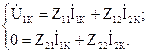
Выразим из второго уравнения ток на выходе четырехполюсника, и подставим полученное выражение в первое уравнение:
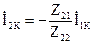, тогда 
.
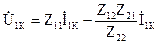Сопротивление замыкания со стороны первичных зажимов:
.
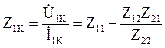Из этого вычислим коэффициенты:
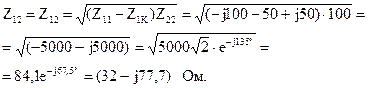
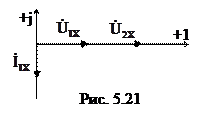5.2.7 Для симметричного четырехполюсника, трудящегося в режиме холостого хода, на рис. 5.21 задана векторная диаграмма токов и напряжений. Выяснить А-параметры четырехполюсника. Действующие значения напряжений и тока: U1Х = 100 В; U2Х = 200 В; I1Х = 2,5 А.
Запишем уравнения четырехполюсника А-формы для режима холостого хода ( ):
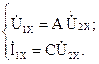
Действующие значения напряжений и тока на зажимах четырехполюсника в режиме холостого хода заданы, а их начальные фазы возможно выяснить по векторной диаграмме. Тогда уравнения четырехполюсника запишутся, как
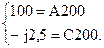
Из этого коэффициенты А = 0,5, С = –j0,0125 1/Ом.
Для симметричного четырехполюсника D = A = 0,5.
Из соотношения, связывающего коэффициенты А-формы AD – BC = 1 определим коэффициент В:
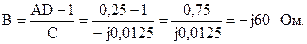
5.2.8 Для ослабления сигнала в нагрузке между источником питания и нагрузкой включен симметричный четырехполюсник. Вычислить параметры Т-схемы замещения, если он нагружен на согласованное сопротивление ZH = ZC = 200 Ом, а сигнал необходимо ослабить на 0,5 Нп без его задержки во времени.
Параметры Т-схемы замещения легко взять через значения коэффициентов А-формы записи уравнений:
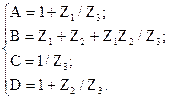тогда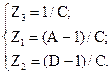 
Определим коэффициенты А-формы, составив уравнения:
A = D, поскольку четырехполюсник симметричный;
е(a+jb) = =e0,5, так как сигнал передается без отлагательств во времени, то коэффициент фазы b = 0; A2 – BC = 1.
Составим совокупность уравнений с тремя малоизвестными коэффициентами:
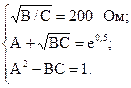
Решаем совокупность уравнений и находим коэффициенты:
А = 1,128; C = 0,0026 1/Ом; B = 10,2 Ом.
По вычисленным значениям коэффициентов определим параметры симметричной Т-схемы замещения:
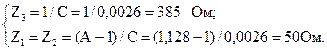
Как видно по значениям взятых комплексных сопротивлений схема разглядываемого четырехполюсника реализована на активных сопротивлениях.
5.2.9 Выяснить параметры П-схемы замещения симметричного четырехполюсника, нагруженного на характеристическое сопротивление ZH = ZC = 500 Ом, благодаря которому осуществляется задержка синусоидального сигнала на четверть периода без его ослабления.
Параметры П-схемы замещения легко взять через значения коэффициентов А-формы записи уравнений:
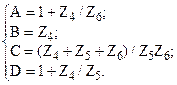откуда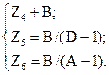 
Определим коэффициенты А-формы, составив уравнения:
A = D, поскольку четырехполюсник симметричный;
е(a+jb) = =ej90°, так как сигнал передается без ослабления, то коэффициент затухания a = 0; так как задержка во времени образовывает четверть периода, то коэффициент фазы b=90°; A2 – BC = 1.
Составим совокупность уравнений:
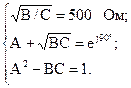
Решив эту совокупность уравнений определим значения коэффициентов А = 0; В = j500 Ом; С = j0,002 1/Ом.
По вычисленным значениям коэффициентов определим параметры симметричной П-схемы замещения:
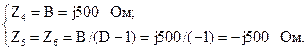
Как видно по значениям взятых комплексных сопротивлений схема разглядываемого четырехполюсника реализована абсолютно на чисто реактивных элементах. В последовательной ветви включена совершенная индуктивная катушка, а в продольных ветвях конденсаторы.
5.2.10Выяснить параметры полосового фильтра, имеющего Т-образную схему (рис. 5.22), нагруженного на характеристическое сопротивление при резонансной частоте. Нижняя граница полосы пропускания кожный покров1 = 750 Гц, верхняя граница полосы пропускания f2 = 850 Гц.
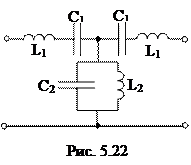
Резонансная частота Гц.
Параметры Т-образной схемы:
