Лабораторная работа №1
по дисциплине:
«Теория автоматического управления»
ОПРЕДЕЛЕНИЕ ВРЕМЕННЫХ И ЧАСТОТНЫХ Черт ТИПОВЫХ ЗВЕНЬЕВ
Вариант 4
Выполнил: ст.гр. 121191
Илюхина И.М.
Проверил: к.т.н., доцент каф. ПУ
Матвеев В.В.
Тула 2012
Цель работы: изучение временных и частотных черт типовых динамических звеньев.
Теоретическая часть
Временные характеристики типовых звеньев
Динамические особенности линейных систем и звеньев автоматического управления смогут быть обрисованы как дифференциальными уравнениями, так и графическими чертями. Процесс нахождения дифференциального уравнения совокупности через уравнения ее элементов в общем случае есть достаточно трудоемким. Изучение САУ значительно упрощается при применении прикладных математических способов операционного исчисления в частности преобразований Лапласа. Преобразование дифференциальных уравнений по Лапласу есть базой очень удобного для изучений САУ способа передаточных функций. Посредством передаточных функций возможно легко оценить динамические особенности любого элемента САУ.
Передаточной функцией W(s) звена (совокупности) именуется отношение преобразования по Лапласу выходной координаты X(s) звена (совокупности) к изображению по Лапласу входной координаты Y(s) при нулевых начальных условиях:
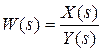 (1)
(1)
Под временными чертями динамического звена (совокупности) в общем случае понимается графическое изображение процесса трансформации выходной величины в функции времени при переходе звена из одного равновесного состояния в второе. Так как дифференциальное уравнение также определяет изменение выходной величины в функции времени при некоторых начальных условиях, то временная черта представляет собой графическую форму ответа дифференциального уравнения звена для принятого типового действия и, следовательно, абсолютно характеризует динамические особенности звена (совокупности).
Переходная функция, либо переходная черта, h(t) обрисовывает переходной процесс на выходе звена (совокупности), появляющийся при подаче на его вход быстрого действия, которое мгновенно возрастает от нуля до единицы и потом остается неизменным при нулевых начальных условиях.
Единичная ступенчатая функция 1(t).Типовое входное действие, при котором функция y(t)=1(t) определяется соотношениями y(t) =0 при t 0 и y(t) =1 при t³ 0, т.е.
0, т.е.
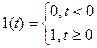 (2)
(2)
именуется единичной ступенчатой функцией 1(t) – рисунок 1а. Предполагается, что единичной ступенчатой функцией 1(t) имеет туже размерность, что и физическая величина на входе звена. В случае, если действие представляет собой неединичную ступенчатую функцию y(t)=ууст.?1(t), выходная величина будет равна x(t)= ууст.h(t).
Ступенчатая функция представляет собой распространенный вид входного действия в САУ. К такому виду сводятся мгновенное изменение нагрузки электрического генератора, мгновенное возрастание нагрузки на валу двигателя, мгновенный поворот командной оси следящей совокупности и т.п. Умножение какой-либо функции времени x(t) на единичную ступенчатую функцию 1(t) свидетельствует, что функция времени x(t) будет существовать лишь при t³ 0, при t 0 она обращается в нуль.
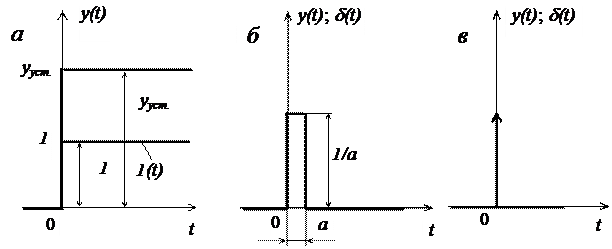
Рисунок 1 – Типовые входные действия
а – ступенчатые функции – единичная и произвольной величины;
б — единичная импульсная функция конечных параметров;
в — единичная импульсная функция нулевой ширины
Единичный импульс – дельта-функция d(t)– это математическая идеализация предельно маленького импульсного сигнала, площадь которого равна единице при длительности равной нулю, и высоте равной бесконечности. Дельта-функция является производной от единичной ступенчатой функции
либо в операционной форме
d(s) = sL[1(t)] = s =1. (4)
Исходя из этого
L[w(t)] = W(s) d(s) =W(s),(5)
т.е. изображение импульсной переходной функции равняется передаточной функции. Из этого, для чёрта динамических особенностей звена (совокупности) в равной мере смогут быть использованы как передаточная, так и импульсная переходная функция. Дельта-функция тождественно равна нулю везде, не считая точки t = 0, где она пытается к бесконечности.
Применение ступенчатого постоянного либо импульсного действия в виде стандартного входного сигнала имеет кроме этого да и то преимущество, что настоящие, любой формы, раздражающие действия на совокупность возможно представить в виде последовательности таких сигналов, к примеру так как продемонстрировано на рисунке 2.

Рисунок 2 – Представление входного действия произвольной формы суммой входных ступенчатых действий
При поступлении на вход звена либо разомкнутой совокупности с передаточной функцией W(p) входной величины y(t) = 1(t) на выходе приобретаем переходную чёрта x = h(t). Входная и выходная величины, преобразованные по Лапласу запишутся следующим образом
Y(p) = L[y(t)] = L[1(t)] = 1/p; (9)
X(p) = L[h(t)] = h(p). (10)
С учетом этих соотношений возьмём:
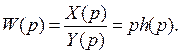 (11)
(11)
Из выражения (11) направляться, что по временной чёрту совокупности (по переходной функции) возможно взять передаточную функцию совокупности. Со своей стороны изображение по Лапласу переходной функции определяется выражением
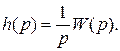 (12)
(12)
Из выражения (12) посредством обратного преобразования Лапласа возможно выяснить переходную функцию разомкнутой совокупности:
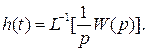 (13)
(13)
Подобно переходная функция замкнутой совокупности имеет форму:
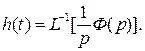 (14)
(14)
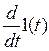 = 1¢(t) (3
= 1¢(t) (3