Аналитическая геометрия
Векторы
Вектором именуется направленный отрезок , где точка — начало, точка — финиш вектора.
Действия с векторами
Суммой векторов и именуют таковой третий вектор , начало которого сходится с началом , а финиш — с финишем при условии, что начало вектора и конец вектора совпадают.
Разностью векторов и именуется вектор таковой, что выполняется условие: .
Произведением вектора на число именуется вектор , удовлетворяющий условиям:
- , в случае, если , , в случае, если .
1.2. Коллинеарные и компланарные векторы
Вектора, параллельные одной прямой либо лежащие на одной прямой именуют коллинеарными векторами
1) Два вектора коллинеарны, в случае, если отношения их координат равны.
2) Два вектора коллинеарны, в случае, если их векторное произведение равняется нулевому вектору.
Подтверждение:
Пускай имеется два коллинеарные вектора a = {ax; ay; az} и b = {nax; nay; naz}. Отыщем их векторное произведение
| a ? b = | i | j | k | = i (aybz — azby) — j (axbz — azbx) + k (axby — aybx) = |
| ax | ay | az | ||
| bx | by | bz |
= i (aynaz — aznay) — j (axnaz — aznax) + k (axnay — aynax) = 0i + 0j + 0k = 0
Вектора, параллельные одной плоскости либо лежащие на одной плоскости именуют компланарными векторами.
1) Три вектора компланарны в случае, если их смешанное произведение равняется нулю.
2) Три вектора компланарны если они линейно зависимы.
3) Вектора компланарны в случае, если среди них не более двух линейно свободных векторов.
1.3. Скалярное произведение векторов и его св-ва
Скалярным произведением двух ненулевых векторов и именуется число, равное произведению длин этих векторов на косинус угла между ними:
Свойства скалярного произведения:
1° — симметричность.
2° . Обозначается и именуется скалярный квадрат.
3° В случае, если , то
4° В случае, если и и , то . Правильно и обратное утверждение.
5°
6°
7°
1.4. Косинус угла между векторами
Углом между двумя векторами, отложенными от одной точки, именуется малейший угол, на что необходимо развернуть один из векторов около собственного начала до положения сонаправленности с другим вектором.
Косинус угла между векторами равен скалярному произведению векторов, поделенному на произведение модулей векторов.
| cos ? = | a·b |
| |a|·|b| |
1.5. Векторное произведение векторов и его св-ва
Векторным произведением ненулевых векторов и именуется вектор , обозначаемый знаком либо , протяженность которого .
Свойства векторного произведения:
1° , тогда и лишь тогда, в то время, когда
2°
3° Модуль векторного произведения равен площади параллелограмма, выстроенного на заданных векторах и (рис. 2), т.е.
4°
5°
1.6. Смешанное произведение векторов и его св-ва
Смешанным произведением трех векторов , , именуется число, равное скалярному произведению вектора на вектор :
Свойства смешанного произведения:
1°
2°
3° Три вектора компланарны тогда и лишь тогда, в то время, когда
4° Тройка векторов есть правой тогда и лишь тогда, в то время, когда . В случае, если же , то векторы , и образуют левую тройку векторов.
5°
6°
7°
8°
9°
10° Тождество Якоби:
1.7. Двойное векторное произведение
Двойное векторное произведение векторов — векторное произведение вектора на векторное произведение векторов и
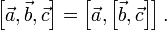
Прямая на плоскости
Уравнение прямой на плоскости в прямоугольной совокупности координат Oxy имеется некое уравнение с двумя переменными x и y, которое обращается в тождество при подстановке в него координат любой точки данной прямой.
Плоскость в пространстве
Любая плоскость в пространстве определяется линейным уравнением
Прямая в пространстве
Прямая в пространстве возможно задана как линия пересечения двух плоскостей. Так как точка прямой прнадлежит каждой из плоскостей, то ее координаты обязаны удовлетворять уравнениям обеих плоскостей, другими словами удовлетворять совокупности из двух уравнений.
Кривые второго порядка
Кривая второго порядка — геометрическое место точек плоскости, прямоугольные координаты которых удовлетворяют уравнению вида
в котором по крайней мере один из коэффициентов отличен от нуля.
Матрицы
Ма?трица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца либо поля (к примеру, целых, настоящих либо комплексных чисел), которая является совокупностью столбцов и строк, на пересечении которых находятся её элементы.
Транспонирование матрицы
Транспонирование матрицы А. Транспонированную матрицу обозначают AT либо A’
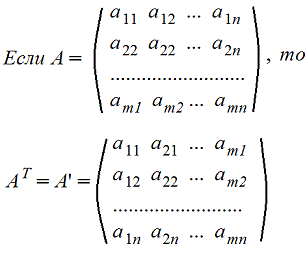
Строки и столбцы поменялись местами
6.3. Обратная матрица
Обра?тная ма?трица — такая матрица A?1, при умножении на которую исходная матрица A даёт в следствии единичную матрицу E:
Свойства обратной матрицы
-
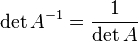, где обозначает определитель. - для любых двух обратимых матриц и .
- , где обозначает транспонированную матрицу.
- для любого коэффициента .
- .
- В случае, если нужно решить совокупность линейных уравнений , (b — ненулевой вектор) где — искомый вектор, и в случае, если существует, то . В другом случае или размерность пространства ответов больше нуля, или их нет вовсе.
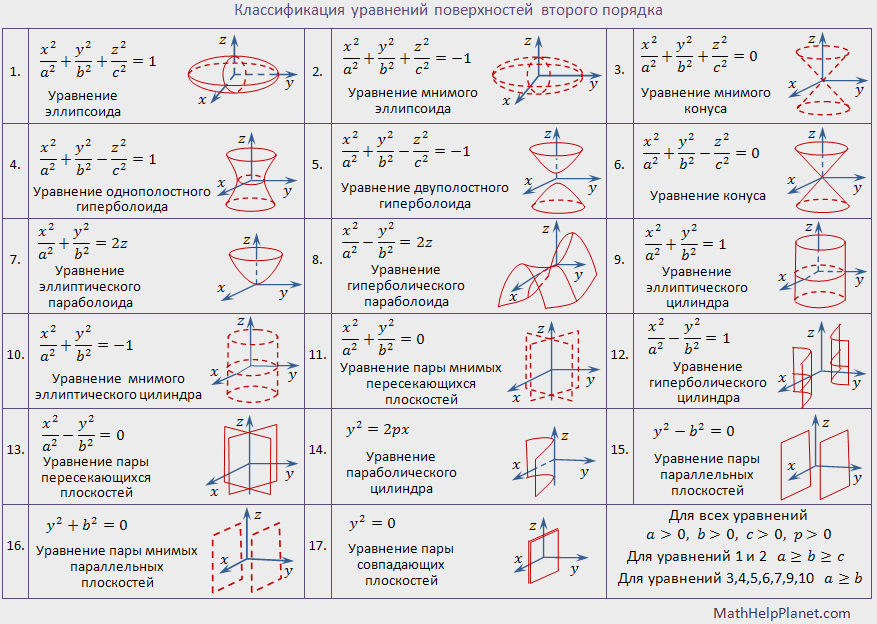
Поверхности второго порядка
Линейное пространство
Лине?йное простра?нство, либо ве?кторное простра?нство, есть обобщением понятия совокупности всех векторов n-мерного пространства.
Квадратная форма и ее св-ва
Квадратичная форма — функция на векторном пространстве, задаваемая однородным многочленом второй степени от координат вектора.
Пускай имеется векторное пространство над полем и — базис в .
Функция именуется квадратичной формой, в случае, если её возможно представить в виде
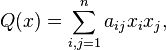
где , а — кое-какие элементы поля .
Свойства:
- Критерий Сильвестра
- Квадратичная форма есть положительно определенной, тогда и лишь тогда, в то время, когда все угловые миноры её матрицы строго хороши.
- Квадратичная форма есть отрицательно определенной, тогда и лишь тогда, в то время, когда символы всех угловых миноров её матрицы чередуются, причем минор порядка 1 отрицателен.
- Для любой невырожденной квадратичной формы существует базис, в котором её матрица диагональна, а сама форма имеет канонический вид:
- Отыскать данный базис возможно при помощи способа Лагранжа.
- Разность между числом хороших ( ) и отрицательных ( ) участников в данной записи именуется сигнатурой квадратичной формы. Сигнатура, кроме этого как и числа хороших и отрицательных слагаемых, не зависят от способов приведения квадратичной формы к каноническому виду (закон инерции Сильвестра).
Аналитическая геометрия
Векторы
Вектором именуется направленный отрезок , где точка — начало, точка — финиш вектора.
Действия с векторами
Суммой векторов и именуют таковой третий вектор , начало которого сходится с началом , а финиш — с финишем при условии, что начало вектора и конец вектора совпадают.
Разностью векторов и именуется вектор таковой, что выполняется условие: .
Произведением вектора на число именуется вектор , удовлетворяющий условиям:
- , в случае, если , , в случае, если .
1.2. Коллинеарные и компланарные векторы
Вектора, параллельные одной прямой либо лежащие на одной прямой именуют коллинеарными векторами
1) Два вектора коллинеарны, в случае, если отношения их координат равны.
2) Два вектора коллинеарны, в случае, если их векторное произведение равняется нулевому вектору.
Подтверждение:
Пускай имеется два коллинеарные вектора a = {ax; ay; az} и b = {nax; nay; naz}. Отыщем их векторное произведение
| a ? b = | i | j | k | = i (aybz — azby) — j (axbz — azbx) + k (axby — aybx) = |
| ax | ay | az | ||
| bx | by | bz |
= i (aynaz — aznay) — j (axnaz — aznax) + k (axnay — aynax) = 0i + 0j + 0k = 0
Вектора, параллельные одной плоскости либо лежащие на одной плоскости именуют компланарными векторами.
1) Три вектора компланарны в случае, если их смешанное произведение равняется нулю.
2) Три вектора компланарны если они линейно зависимы.
3) Вектора компланарны в случае, если среди них не более двух линейно свободных векторов.
1.3. Скалярное произведение векторов и его св-ва
Скалярным произведением двух ненулевых векторов и именуется число, равное произведению длин этих векторов на косинус угла между ними:
Свойства скалярного произведения:
1° — симметричность.
2° . Обозначается и именуется скалярный квадрат.
3° В случае, если , то
4° В случае, если и и , то . Правильно и обратное утверждение.
5°
6°
7°
1.4. Косинус угла между векторами
Углом между двумя векторами, отложенными от одной точки, именуется малейший угол, на что необходимо развернуть один из векторов около собственного начала до положения сонаправленности с другим вектором.
Косинус угла между векторами равен скалярному произведению векторов, поделенному на произведение модулей векторов.
| cos ? = | a·b |
| |a|·|b| |
1.5. Векторное произведение векторов и его св-ва
Векторным произведением ненулевых векторов и именуется вектор , обозначаемый знаком либо , протяженность которого .
Свойства векторного произведения:
1° , тогда и лишь тогда, в то время, когда
2°
3° Модуль векторного произведения равен площади параллелограмма, выстроенного на заданных векторах и (рис. 2), т.е.
4°
5°
1.6. Смешанное произведение векторов и его св-ва
Смешанным произведением трех векторов , , именуется число, равное скалярному произведению вектора на вектор :
Свойства смешанного произведения:
1°
2°
3° Три вектора компланарны тогда и лишь тогда, в то время, когда
4° Тройка векторов есть правой тогда и лишь тогда, в то время, когда . В случае, если же , то векторы , и образуют левую тройку векторов.
5°
6°
7°
8°
9°
10° Тождество Якоби:
1.7. Двойное векторное произведение
Двойное векторное произведение векторов — векторное произведение вектора на векторное произведение векторов и
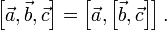
Прямая на плоскости
Уравнение прямой на плоскости в прямоугольной совокупности координат Oxy имеется некое уравнение с двумя переменными x и y, которое обращается в тождество при подстановке в него координат любой точки данной прямой.
Виды уравнений прямой на плоскости
Неспециализированное уравнение прямой:
Уравнение именуется неспециализированным уравнением прямой на плоскости.
Обычный вектор прямой, заданной неспециализированным уравнением прямой вида , имеет координаты .
Уравнение прямой в отрезках:
Уравнение прямой вида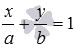 
, где a и b – кое-какие настоящие числа хорошие от нуля, именуется уравнением прямой в отрезках.
Каноническое уравнение прямой:
Каноническое уравнение прямой на плоскости в прямоугольной декартовой совокупности координат Oxy имеет форму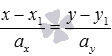 
, где 
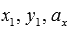и – кое-какие настоящие числа, причем и в один момент не равны нулю.
Со своей стороны числа и , стоящие в знаменателях дробей, представляют собой координаты направляющего вектора данной прямой.
Параметрическое уравнение прямой:
Параметрические уравнения прямой на плоскости имеют вид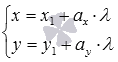 
, где 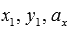и – кое-какие настоящие числа, причем и в один момент не равны нулю, а — параметр, принимающий каждые настоящие значения.
Обычное уравнение прямой:
В случае, если в общем уравнении прямой вида числа А, В и С таковы, что протяженность вектора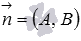 
равна единице, то это неспециализированное уравнение прямой именуется обычным уравнением прямой. Обычное уравнение прямой определяет в прямоугольной совокупности координат Oxy прямую линию, обычным вектором которой есть вектор 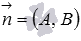, причем эта прямая проходит на расстоянии от начала координат в направлении вектора .
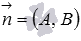2.2. Обоюдное размещение прямых на пл-ти
Теорема. Пускай
и
– неспециализированные уравнения двух прямых на координатной плоскости Оху. Тогда
1) в случае, если , то прямые и совпадают;
2) в случае, если , то прямые и
параллельные;
3) в случае, если , то прямые пересекаются.
2.3. Угол между прямыми на пл-ти
Угол ? между двумя прямыми, заданными неспециализированными уравнениями A1x + B1y + C1 = 0 и A2x + B2y + C2 = 0, вычисляется по формуле:
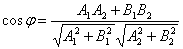
Угол ? между двумя прямыми, заданными уравнениями с угловыми коэффициентами y = k1x + b1 и y2 = k2x + b2, вычисляется по формуле:
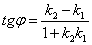
Угол ? между двумя прямыми, заданными каноническими уравнениями (x-x1)/m1 = (y-y1)/n1 и (x-x2)/m2 = (y-y2)/n2, вычисляется по формуле:
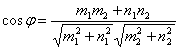
2.4 Расстояние от точки до прямой на пл-ти
В случае, если задано уравнение прямой Ax + By + C = 0, то расстояние от точки M(Mx, My) до прямой возможно отыскать, применяя следующую формулу
| d = | |A·Mx + B·My + C| |
| vA2 + B2 |
Плоскость в пространстве
Любая плоскость в пространстве определяется линейным уравнением