Для доказательства увидим, что по лемме 1 п. 32.2 оператор Ф удовлетворяет в Q условию Липшица с постоянной q е е(0, 1), т. е. есть в Q сжатием.
33.3.Использование к совокупностям линейных алгебраических уравнений. Способ сжимающих отображений находит бессчётные фактически серьёзные приложения кроме того при линейной совокупности m уравнений с m малоизвестными, в особенности в то время, когда m громадно и использование правила Крамера не нужно. Тут мы остановимся на двух известных способах ответа совокупностей линейных уравнений.
Пускай Н — т-мерное унитарное пространство, у — заданный вектор в Я, а Для нахождения ответа уравнения
х — Вх = у (П
довольно часто используется так называемый способ несложной итерации (см. [1]). Наряду с этим ответ уравнения (1) разыскивается как предел последовательности
хп+1 = Вхп + у, п = 0,1,…, (2)
а начальное приближение хо задано. В случае, если хп-»-х при л-оо (х„ — ответ (2), а х — ответ (1)), то говорят, что способ несложной итерации сходится.
С позиций принципа сжимающих отображений уравнение (1) направляться записать в виде дг = Ф(дг), где Ф (х) = Вх + у. Наряду с этим
|| Ф ([6]’) — Ф (*) || = || Вх’ — Вх || || В || || — х ||.
В случае, если ||В|| 1, то оператор Ф есть сжимающим и способ несложных итераций сходится. Более неспециализированное условие его сходимости дает теорема 2 п. 33.2, в то время, когда сжимающим есть оператор Ф* при некоем натуральном k. Предлагаем читателю проверить, что в этом случае
k
ф* (х) = в*х+Е в1 у
/ = 0
и, следовательно,
|| Фк (*’) — Фк (х) || || Вк || || — х ||.
Так, в случае, если удастся продемонстрировать, что при каком-либо k ||Bfe|| 1, то, в соответствии с теореме 2 п. 33.2, способ несложной итерации сходится. На этом пути удается взять следующее нужное и достаточное условие (см. [1]).
Теорема. Для сходимости способа несложной итерации при любом начальном приближении нужно и достаточно, дабы все личные значения оператора В по модулю были меньше 1.
Подтверждение достаточности. Пускай Яь ,.. …, Хт — личные значения оператора В (среди них смогут быть равные). В соответствии с условию теоремы существует число
|Яг К
Фиксируем число б 0 так малое, что
~lBei = Я16-1е1, 6-1Ве, = Я;б-1ег + г = 2, …,т,
где или аг-i = 0, или — 1. По окончании умножения на б приходим к равенствам
Вех = Ххеь Bei = %iel-{-bai_lei_u г = 2, т. (3)
Заберём х е Н, и пускай его разложение по базису имеет
вид
т
Пользуясь формулами (3), возможно продемонстрировать, в соответствии с математической индукции, что
т т— 1
Bx—Y, Kli^i + 6 ? а;1г + 1
г=i i=i
m m—1 m—2
b2x = Z Aft*, + 26 2 A + б2 У a?i+qet, (4)
l — l I I » /
m m—I m—
Фа + С», I +Z
где Cm — биномиальные коэффициенты. Наряду с этим, в случае, если m^s то полагаем
Отыщем в памяти сейчас, что | ^
| I |
I m—s II m—s
11 s
где
| C |
m Sl/2 / m ч 1/2
Slid2] У^И2; • (6)
Оценка (4) с применением (5) ведет к следующему неравенству:
|]B**ll
Увидим сейчас, что функционал а(х), определяемый формулой (6), удовлетворяет всем теоремам нормы. Но Н конечномерно, и потому все нормы в Я эквивалентны. Исходя из этого найдется постоянная О 0 такая, что для всех л:е// имеем c||jc||. Обращаясь к (7), приобретаем оценку
т. е. c(q + b)k. Так как
громадном k будем иметь ||?ft]| 1, и способ несложной итерации сходится.
Подтверждение необходимости. Пускай X собственное значение В и 1. Пускай
х\ — Вх о + У — Вх + У + М = х + Яф,
х2 = Вхх + у = х + №у, *rt = * + Aq.
При | Я хп-/*хпри п-*- оо, и, следовательно, способ итерации расходится. Теорема доказана.
Замечание I. В случае, если В — самосопряженный оператор в Я,
то ||S]| =max 11 ^ q 1 (см. следствие к теореме п. 23.4) и 1
оператор Ф (х) = Вх + у — сжимающий.
Замечание 2. Теорему возможно перефразировать так: чтобы спектральный радиус г0(В) оператора В был меньше 1 (см. п. 24.2), нужно и достаточно, дабы все собственнее значения В были по модулю меньше 1.
Разглядим сейчас способ верхней релаксации (см. [14]). Для решения линейного уравнения
Ах = у, (8)
где у е Н, А ^ 2(H), Н — m-мерное унитарное пространство, в большинстве случаев употребляются разные варианты его записи в форме (1). Обрисуем один из них. Пускай в Н фиксирован ортонормиро- ванный базис, в котором (4) есть матричной записью совокупности линейных уравнений:
*=(ЫГ г/ = ЫГ A = (an)7.i=v
Предположим, потом, что оператор А вещественный самосопряженный, т. е. Oil вещественны и ач = а;1, и положительно определенный, т. е. (Ах, х) 0 при х ф 0. Разложим матрицу А на сумму трех матриц:
Л = С + Л + 0, (9)
где матрица С — нижняя левая треугольная, матрица D — верхняя правая треугольная, а Л — диагональная матрица. Правильнее, с?/ = ац при i j, сц — 0 при i ^ /; Я„ = аи, %ц = О при i ф у, dij = Chi при i }, а^ = 0 при i ^ /’. Запишем уравнение (8) в виде
(Л + «вС)ж = [(1 —
где со 0. Потому, что матрица Л + со С обратима, то уравнению (10) возможно придать вид
х = Вах -f со (Л + мС)-1 у, (11)
где Вш = (Л + соС) [ (1 — со) Л — coD].
Продемонстрируем, что при 0 со 2 все личные значения матрицы В(о по модулю меньше 1. Вправду, в случае, если Я— ее собственное значение, а ф — отвечающий Я ее личный вектор, то
[(1 — со) Л — ©D] ф = Я (Л + юС) ф. (12)
Учитывая представление (9), уравнения (12) возможно записать в виде
[(2 — ©) Л — юЛ + ю (С -Чр)] ф = Я ((2 — ©) Л + coy* + со (С — ?)] ф. J)96
Умножим это равенство скалярно на ф и, пользуясь тем, что ((С — D)ф, ф) = 0, возьмём
, _ (2 — ю) (Лф, ф) — to (Лф, ф) (2 — (в) (Лф, ф) + (о (Лф, ф) 1
Так как (Лф, ф)0 и (Лф, ф) 0, то при со е (0, 2) имеем ]Л| 1. В соответствии с способу несложных итераций, способ верхней релаксации, т. е. способ последовательных приближений для уравнения (11), сходится при любом начальном приближении, в случае, если О
33.4.единственности решения и Теоремы существования задачи Коши для дифференциального уравнения в банаховом пространстве. Принцип сжимающих отображений разрешает дагь простое подтверждение разных теорем о единственности и существовании ответа задачи Коши для дифференциальных уравнений.
Мы разглядываем тут дифференциальные уравнения в банаховом пространстве, потому, что доказательства в этом случае нисколько не усложняются, а абстрактная запись разрешает охватить более широкий класс прикладных задач. Обращение отправится о дифференциальном уравнении вида
^ = F(t,x), (1)
где F(t,x)—нелинейный оператор от двух переменных: вещественного переменного /^0 и переменного х из вещественного банахова пространства X; значения F кроме этого лежат в X. Для уравнения (1) ставится задача Коши, т. е. задается начальное условие (а е X)
х 1г_о = а. (2)
Теорема 1. Пускай F(t,x) постоянен по t на [0,0] при каждом фиксированном х с \\х — .хоИ^’ при t е [0, 0] их таких, что IU — удовлетворяет следующим условиям:
JI F (/, х) || ^ с, (3)
||F(t, Xl)-F(t, х2)||
Тогда на [0, 8j], где
01 = min± 0), (5)
существует единственное ответ x(t) задачи Коши (1) — (2), Наряду с этим на [0, 0i] ||jc (/)— *о1К г.
Подтверждение. Пускай x'(f)—ответ задачи (1)— (2), т. е. непрерывно дифференцируемая на некоем [0, 0i], Gi ^ 0, абстрактная функция, обращающая (1) в тождество на [0,01 ] и удовлетворяющая начальному условию (2). Под- ставим x{t) в (1) и полученное тождество проинтегрируем на [О,/] с учетом (2). Возьмём, что x(t) удовлетворяет следующему интегральному уравнению:
t
х (0 = а + J F (s, х (s)) ds. (6)
о
Обратно, пускай x(t)—постоянное на [0,9i] ответ интегрального уравнения (6). Увидим сперва, что при se[0,0i] абстрактная функция F(s,x(s)) постоянна на [0,0i]. Это вытекает из непрерывности x(s), непрерывности F(t,x) по t и следующей оценки, применяющей условие Липшица (4):
|| F (s, х (s)) — F (s0, х (so)) IK IIF (s, x (s)) -F(s,x (s0)) || +
+ || F (s, x (so)) — F (so, x (s0)) IK m || * (s) — * (s0) II +
+ || F(s, x(so))-F(so, x(s0))f
В случае, если s, s0e[0, 0i] и s-s0, то правая часть в последнем неравенстве пытается к нулю и, значит, F(s,x(s)) постоянна в каждой точке [О, Эi]. Отсюда вытекает, что в соответствии с (6) лс(0)=а, и дифференцируемость х(/) на [0, 6i] и равен ство x'(t) = F(t,x(t)) (см. свойство 8 п. 25.2). Итак, x(i) — ответ задачи (1) — (2). Так, задача нахождения ответа задачи Коши (1) — (2) эквивалентна задаче нахожде ния постоянного ответа интегрального уравнения (6). Пользуясь этим, введем банахово пространство Cx[0, 9i] абстракт ных, постоянных на [0, 0i] функций x{t) со значениями в X и с нормой
\х(01 = max ||х (0II.
[о, 0,]
Разглядим в Cx[0, 9i] замкнутый шар
Sr (а) = {х (0 е Сх [0, 6J; ||х (/) — a IK г). Нелинейный оператор
Ф(х) = а + \F(s, x(s))ds(7)
о
переводит Sr(a) в себя, потому что
t I t
[F(s, х (s)) ds шах [ || F (s, x (s)) || ds
| Ф (x) —a| = max
| о « №.ej |
10, 8,]
благодаря неравенства (3) и определения 0[ равенством (5). Помимо этого, Ф(х) есть на Sr{a) оператором сжатия, так
как в соответствии с (4)
| Ф (jci) — Ф(лг2)| = тах [о, ej
t
\[F{s, xl (s))-F(s, x2(s))]ds
0 II
max \ IIF (s, xx (s)) — F (s, x2 (s)) || ds [o, преисподняя J
где q = 0i, m 1 (см. (5)).
В соответствии с принципу сжимающих отображений в шаре Sr(a)1 существует единственное ответ С*[0,0i] уравнения
(6). Так,теорема 1 доказана.
Определенным недочётом взятого результата есть то событие, что ответ x(t) задачи (1) — (2) выяснено не на всем [0, 0], а только локально на [0, 0i], где 01 удовлетворяет равенству (5). Пример задачи Коши для обычного дифференциального уравнения dxjdt — x2, х(0)=1, правильное ответ которой имеет форму х (I) — _ -, говорит о том, что
в общем случае нельзя гарантировать существования ответа задачи (1) — (2) «в целом»—на всем [0,0].
При более твёрдых догадках относительно оператора F{t,x) удается доказать теорему единственности и существования ответа задачи Коши (1) — (2) на [0,0].
Теорема 2. Пускай оператор F(t,x) постоянен по t на [0, 0] при каждом фиксированном х е X и удовлетворяет условию Липшица (4) при этих же значениях переменных. Тогда на [0,0] существует единственное ответ задачи Коши (1)—¦ (2).
Мы приведем ниже два доказательства теоремы 2, каждое из которых достаточно легко и поучительно.
Подтверждение 1. Как и в доказательстве теоремы 1, сведем задачу (1) — (2) к эквивалентному интегральному уравнению (6). Разглядим в банаховом пространстве С*[0, 0] интегральный оператор Ф(х), определяемый равенством (7), Имеем следующую оценку:
t
[Ф (*,) — Ф (х2}| m ^ || (s) — х2 (s) || ds mt | xi — х21, о
применяя которую находим
t
|| Ф2 (*,) — Ф2 (х2) II m $ IIФ (*, (s)) — Ф (х2 (s)) II ds
о
t
m2 ^ s II Xl (s) — х2 (s) II ds ~2j I Xl — x2 [.
Продолжая такие оценки, способом полной математической индукции устанавливаем оценку
II Ф (*,) — Ф (х2) [К-^ |*i — х2|. Переходя к максимуму на [0, 0], возьмём
|Ф(х,) — Ф(х2)К|х, — х21.
Потому, что (mQ)n/nl -*• 0 при я-»- оо, то, фиксируя так громадное п, дабы (mQ)a/n\ = q 1, заключим , что Фя — сжатие в С* [0, 0]. Утверждение теоремы 2 направляться сейчас из теоремы 2 п. 33.2.
Подтверждение 2. В банаховом пространстве С*[0,0] введем эквивалентную норму
I * if) lm = max II e~mix (0 [|.
[0. ei
Продемонстрируем сейчас, что интегральный оператор Ф есть сжатием в смысле данной новой нормы. Вправду, t
|| Ф (х,) — Ф (х2) IK т $ II Xi (s) — х2 (s) I, e-msems ds о
t
m J ds || x, — x2 ||m = (emi — 1) |x, — x2|m.
о
Умножив полученное неравенство на e~mt, возьмём
e~mt IIФ (х.) — Ф (х2) IK (1 — e~mt) | х, — х2|т.
Наконец, перейдем к шах на [0,0], что дает неравенство
| Ф (х,) — Ф (х2) (1 — е-9) IX! — х2 \т.
Итак, Ф — сжимающий оператор. Теорема 2 доказана. Упражнение. Перефразируйте теоремы 1 и 2:
а) на случай обычного дифференциального уравнения,
б) на случай совокупности I обычных дифференциальных уравнений с I малоизвестными функциями.
Разглядим задачу Коши для линейного дифференциаль- t ного уравнения в банаховом пространстве:
=A(t)x + y(t), t 0, х (0) = а. (8)
Пускай y{t)] и A(t)—соответственно абстрактная функция со значениями в X и оператор-функция из (Х), постоянные на m+.ooh,
Потому, что на каждом [0,8] шах|]Д (0 И
§ 34. Итерационный процесс Ньютона
34.1. Описание итерационного процесса Ньютона. Ньютон внес предложение действенный способ вычисления ответов уравнения
F(x) = 0 ‘ (1)
для случая функции F(x) с вещественными значениями, зависящей от вещественной переменной х. Потом способ Ньютона был перенесен на совокупности уравнений (в то время, когда F(x)^Em, х^Ет), а после этого обобщен в работах акад. Л. В. Канторовича на уравнения в банаховых пространствах.
Пускай F(x) — нелинейный оператор, определенный в окрестности S решения х* уравнения (1), непрерывно дифференцируемый в не сильный в смысле Фреше. Пускай, потом, в S оператор F'(x) непрерывно обратим. Итерационный процесс Ньютона пребывает в следующем. Выбирается начальное приближение Хо е 5 и лежащее достаточно близко к ответу х*. Предстоящие приближения хп, п= 1,2, …, предлагается вычислять по формуле
Хп = Хп-1 — [F’ (*n-i)r’ F (*„_i), п= 1,2,… (2)
В книге [11] (гл. XVIII) читатель может отыскать подробнейшим образом созданную теорию способа Ньютона, разные варианты теорем о сходимости итерационного процесса (2) и родных к нему процессов, и бессчётные приложения. Способ Ньютона есть на данный момент одним из самые употребительных вычислительных способов. Основное его преимущество — это (в определенных догадках) весьма стремительная сходимость последовательных приближений (2) к ответу х*. Способ применим кроме этого и при, в то время, когда уравнение (1) имеет пара ответов.
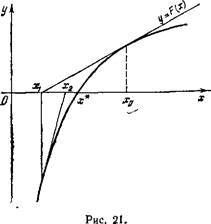
Дадим описание способа Ньютона в несложных случаях. Пускай сперва х — вещественная переменная и значения F{x)’ кроме этого вещественны. Предположим, что в окрестности ответа х? (рис. 21) функция F(x) строго возрастает и выпукла вверх (подобно рассматриваются и другие случаи строго монотонной и выпуклой функции). Выберем начальное приближение Хо достаточно близко к х*. Запишем уравнение касательной к кривой y = F(x) в точке (xq,F(xq)): у = F(х0) + F'(х0) {х — х0). Точка пересечения касательной с осью абсцисс окажется при у = 0. Ее абсцисса равна значению, вычисляемому по формуле (2) при п = 1. Потом проводим касательную к кривой у = F(x) в точке (xi, F(xi)) и приобретаем х2 (см. (2) при п = 2) и т. д. В следствии получается последовательность {х„}, весьма скоро сходящаяся к х*, в случае, если — достаточно мало. В разглядываемом случае способ Ньютона в большинстве случаев именуют способом касательных Ньютона.
Пускай сейчас х, F(x)^Em. В случае, если ft(xь …, хт), ?= 1, … …, п, — координатные функции F(x), то уравнение (1) есть краткой записью совокупности уравнений
* „. . fi(x ь …. Хт) = 0, i= 1…………………….. т.
Производная F’ (я) = ~ это матрица Якоби, а
|
|[Р(л:)]-1 — обратная матрица. Формулы (2) воображают собою, так, матричную запись итерационного процесса Ньютона в Ет.
34.2. Теорема о сходимости итерационного процесса Ньютона. Приведем один из самые удобных в приложениях вариантов теорем о способе Ньютона. Существование ответа х* тут не планируется, а доказывается. Вопрос о единственности ответа в разглядываемом шаре тут не обсуждается.
Теорема. Пускай в шаре Sr(x0) оператор F(x) дифференцируем и его производная удовлетворяет в этом шаре условию Липшица с постоянной I. Пускай, потом, в S 0 такая, что в Sr(xо)
|[F’Wr1
Пускай, потом, || F (*o) |К ч. Тогда, в случае, если q = -^m2lr\ 1 и
r’ = m4+fq2k-\
А-О
то уравнение F(x) = 0 имеет ответ х* е Sr’ (*о) к которому сходится итерационный процесс Ньютона, начатый с х0. Скорость сходимости хп к х* дается неравенством
2П-1
II хя — х* || mil —-у-.
1 — Q
Подтверждение. Введем для краткости следующие обозначения: ‘
r(x) = [F'(x)r\ Г„ = Г(4 Fn = F(xn), Fi = F'(xn).
Итерационный процесс Ньютона в этих обозначениях записывается так:
xn+i = x„ — YnFn, п = 0, 1, 2, … (3)
Продемонстрируем сперва, что {х„} с: Sr {ха), xi — xq = TqFq и, сле- довательно, ||хх — х0IKтц. Из (2) направляться, что xi
F^Fi — Fo — F’0 (jc, -x0) = F (ж,) — F (лг0) — F’ (xQ) (xt — x0). Пользуясь неравенством (3) п. 32.2, приобретаем
11^1 IK у/II xi — xo IP.
Предстоящие рассуждения совершим способом полной математи- ческой индукции. Пускай уже доказано, что хп s Sr’ (хо) и что честны оценки
\\Xn-Xn-iW
II fJK^ 1\\Хп-Хя-Х II2. (5)
Продемонстрируем, что тогда
lUn+i — *n IK ттде2-1, (о) откуда хп е Sr’ (*о), и что
||/-„+11К|Л1*„+1-лгп||2. (7)
Вправду, из (3), (1) и (4) имеем
II *„+! — *!. II = II № IK Ш || F„ IK у ml || *„ — ||2
Формула (6) доказана. Потом, из (3) имеем
Fn + F’n {Хп+1~Хп) = 0.
Это разрешает оценить Fn+i: Fn+i: Fn+i — Fn — F’n (xn+i — xn) =
= F (*«+i) — F (x„) — F’ (xn) (xn+i — xn). Следовательно, по неравенству (3) п. 32.2
II II II *„ + !-*„ IP,
и неравенство (7) также доказано.
Сейчас установим фундаментальность {хп}. Из оценок и неравенства треугольника (6) имеем
II Хп + р Хп II ^ II хп+р Я/г + р-1 II 4 II — Хп+р_2 II + …
п+р—1
… +||*„+1 — *„||
k=n
Из этого ||х„+р — лг„ || — 0 при п-* оо равномерно по р, поскольку
оо
последовательность 2 Я2*’1 сходится. Итак, {*„} — фундаментальная, а в силу
полноты X — сходящаяся. Обозначим через х* ее предел. Благодаря замкнутости Srr (х0), так как {х„} cz Sr’ (х0), тои/е Sr’ (*о).
Докажем, что х*— ответ уравнения F(x) = 0. Для этого достаточно перейти к пределу при гс-оо в равенстве (3). Приобретаем х* — х* — Г(х*)F(x*), откуда F(x*)= 0, так как Г(х*) обратим. Переходя в оценке (8) к пределу при р -*¦ оо, возьмём следующую оценку скорости сходимости {хл} к х*\
||х%-х„||
Воспользуемся сейчас элементарным неравенством 2I+S 1 + s, честным для s = 0,1, … Полагая в (9) k = п + + s, учитывая, что
II х- — х„ || тц ? Я2*’-1 mm2*-1 ][У= •
s=0 s-0 1 — 1
Теорема абсолютно доказана.
34.3.Модифицированный способ Ньютона. Разглядим видоизменение, либо, как говорят, модификацию, итерационного способа Ньютона:
= xn-[F'(x0)rlF(xn), « = 0,1,2,… (I)
Преимущество формул (1) содержится в том, что упрощаются вычисления (обратный оператор вычисляется лишь один раз). Недочёт формул (1), как мы заметим ниже, пребывает в том, что ухудшается если сравнивать с итерационным способом Ньютона скорость сходимости.
Теорема. Пускай в шаре Sr(xо) оператор F(x) дифференцируем и его производная удовлетворяет в Sr(xo) условию Липшица с постоянной I. Пускай F'(xо) непрерывно обратим и II [f (*о)]~М1 ^ т. Пускай, помимо этого, ll/^xo) IK л- Тогда, в случае, если 2 т21ц 1 и
(2)
то уравнение F(x) = 0 имеет единственное ответ х* е Sr (xq), к которому сходится модифицированный итерационный процесс Ньютона (1), начатый с Хо. Скорость сходимости хп к х* дается неравенством
и . ____
Подтверждение. Продемонстрируем сперва, что оператор Ф(х) = х— [/*’ (лг0) ]—’Z7 (jc) отображает шар Srr (хо) в себя. Вправду, применяя оценку для [F’ (х0) ]неравенство (3) п. 32.2, неравенство треугольника и оценку для F(xo), приобретаем
II Ф (х) — хо II = | [F’ (х0)Г’ [F (х) — F’ (хо) (х — х0)] II
т || F (х) — F (хо) — F’ (х0) (* — х0) + F (х0) II
т || F (х) — F (х0) — F’ (х0) (х — х0) II + т || F (х0) ||
потому что г’ — мельчайший корень квадратного уравнения (см. формулу (2))
-J- mlr’2 — г’ ¦+ тц = 0.
Продемонстрируем сейчас, что в Sr'{x0) оператор есть сжатием. Имеем следующую оценку:
IIФ’ (*) II ¦= II / — \F’ (хо)Г1 F’ (х)|| = J [F’ (хо)]1 [F’ (xq) -F’ (x)]fl
/и/1| х — Хо IK ftilr’ = 1 — V1 — 2m2lx] 1.
Итак, в Sr’ (хо) выполнены условия принципа сжимающих отображений, откуда и вытекают.утверждения теоремы о единственности и существовании ответа х* в Sr (х0) и о сходимости к нему {хл}. Потом,
В соответствии с оценке (2) п. 33.2 скорости сходимости способа последовательных приближений имеем
IU,Хо и Г тп,
1 —
и, так,теорема доказана.
34.4. Пример к способу Ньютона. Разглядим следующую краевую задачу
— х + f (t, х) = 0, 0 / 1, (1)
*(0) = ао, д:(1) = а1. (2)
Предположим для простоты, что функция f{t,x) постоянна совместно со своей личной производной fx(t,x) в полосе 1],
л:е(—со, +оо). Задачу (1) — (2) представим в операторном виде. Для этого введем сперва банаховы пространства X = = С2[а, Ь] и У = С[а, Ь] 4- Е2. Норму в X и в У зададим формулами
|] х ILr = max |л: (о I + max | х (/) |, 10. 11 10, 1]
|| у Ну = max \h (t) | + [0,11 v
где у = {h(t); ао, a,}
Пускай потом F(x)—нелинейный оператор, действующий из X в У по формуле
F (*) = {- (t) + f(t,x (0); * (0) — Оо, X (1) — a,}. (3)
Сейчас задача (1) — (2) записывается в виде операторного уравнения F{x) = 0. Потом нетрудно убедиться, что уравнение F'(x) -z = у, где F'(x) — производная Фреше оператора F в точке х, представляет собой следующую линейную краевую задачу:
~z + fx{t, x{t))z = h(t), z (0) = cto, z(\) = a,. (4)
Следовательно, выражение F'(x)z задается формулой
F’ (х) z = {- z (t) + fx {t, x (/)) z (/); z (0), z (1)} (5)
Но тогда
. F’ (u) z-F'(v)z = {[fx (i, и (/)) — fx (t, v (/))] z (0; 0, 0} и, следовательно,
|| F’ (u) — F’ (v) ||= тах|*/Л (t, и (/)) — fx (t, v
io,H
Перейдем к рассмотрению итерационного процесса Ньютона. Пускай мы имеем достаточно хорошее начальное приближение
*oW решения задачи (1) —(2), т. е. ||F(x0)IK т], где т|-=дотянувшись совершенно верно мало. В соответствии с формуле (3) это указывает, что
шах | (() + / (I, хо (/)) I + У(*о(0)-яо)2 + (*о(1)-а1)2 л (7) [0. 1]
Разглядим в пространстве X шар S/(jt0)’, т. е. множество всех тех x(t)^Xr для которых выполняется неравенство
max | лг (0 — х0 (t) | + max | х (0 — 4 (t) \ г, [о. и [о, п
и предположим, что для всех и и а из этого шара, выполняется неравенство
|hit, U(t))-fx(t, v(t))\^l\u(t)-v(t)\. (8)
В соответствии с равенству (5) тем более в Sr(xo) будет выполняться условие Липшица: l|.F'(u)—Р(и)||^/||и — и||. Потребуем, наконец, дабы при всех j:eSr(^o} для ответов z задачи (4) выполнялась априорная оценка
+ (9)
Тем самым, в Sr(xo) гарантирована оценка || [^'(х)]-1!!^ т и узнан суть постоянных /, г| и т, входящих в формулировки теорем п. п. 34.2 и 34.3 о способе Ньютона.
Выпишем сейчас формулы последовательных приближений. Тут эргономичнее записать формулы итерационного процесса Ньютона в виде
F’ (х„) xn+i = F’ (хп) хп — F (хп.), п = 1, 2, …
Применяя формулы (3) и (5), приобретаем последовательность линейных краевых задач
— -Си + fx (* xn(t))xn+l = fs(t, xn(i))xn{t)-f(t, xn(t))
Xn+i(0) = Oo. *n+i(l) = ®i. « = 0, 1,2,…
Увидим, что полугенная линеаризация задачи (вместо нелинейной задачи решается последовательность линейных задач) еще не решает эту задачу фактически. Для’ решения оказавшихся линейных задач в большинстве случаев приходится прибегать к разностным способам либо к способу Галёркина.
Подводя итог выпишем формулы модифицированного процесса Ньютона:
—
^/i+i(0) = a0, xn+i (1) = ab « = 0,1,2,…
Упражнение. Для краевой задачи примем xo'(t) = 0. Отыщите модифицированным итерационным процессом Ньютона xi(t) и x2(t).
Пускай в данной же задаче xq{t) = t. Отыщите x{(t)y.
Принцип Шаудера
В этом параграфе мы остановимся еще на одном принципе неподвижной точки, принадлежащем Ю. Шаудеру. Наровне с принципом сжимающих отображений и с итерационным мето- дом Ньютона принцип Шаудера есть одним из главных способов доказательства теорем существования ответов нелинейных уравнений.
35.1. Теорема Броуэра о неподвижной точке. Начнем со следующего элементарного примера. Пускай f(x)—постоянная на [0, 1] функция, отображающая [0, 1] в себя, т. е. для всех х е е[0, 1] 1. Продемонстрируем, что в этом случае существует
на [0, 1] неподвижная точка х0 отображения т. е. f(xо) = Хо. Вправду, разглядим на [0,1] функцию 0и /(1) 1, то ф(0)0,и мы можем воспользоваться теоремойо промежуточных значениях (см. [18]), в соответствии с которой найдется точка ?е(0, 1), в которой ф(Е) = 0, т. е. /(?)=?. Итак, существование неподвижной точки отображения f в рассмотренном случае доказано.
Упражнение 1. Продемонстрируйте, что функция Дх) = 2jc(I—х) отображает [0, 1] в себя. Отыщите ее неподвижные точки на [0,1].
Оказывается, рассмотренный пример возможно обобщить на л-мерный случай.
JI. Броуэр доказал следующую теоремуо неподвижной точке.
Теорема 1 (Броуэр). Пускай оператор А отображает единичный шар S={x^En: 1} n-мерного евклидова пространства Еп в себя. Тогда в S найдется неподвижная точка оператора А.
Подтверждение данной теоремы Броуэра в большинстве случаев применяет узкие топологические мысли (см. [21], [12]), но в [8] (см. стр. 505—508) приведено ее подтверждение, основанное на способах матанализа в Еп. Все знакомые нам доказательства теоремы Броуэра достаточно сложны, и останавливаться тут на них мы не будем. Нам пригодится маленькое усиление теоремы Броуэра. Введем сперва пара понятий выпуклого анализа (см. п. 1.7).
Определение 1. Пускай в банаховом пространстве X задано множество М из конечного числа элементов
М = {х(
п
Множество всевозможных линейных комбинаций ? А
i-l
л
Бее и = именуется выпуклой оболочкой мно-
i~l
жества М и обозначается Со (М).
Упражнение 2. Докажите, что множество Со(М), где А1 задается формулой (1), выпукло и замкнуто.
Упражнение 3. Докажите, что в случае, если в (1) е D, i = = 1, … , л, где множество D выпуклое, то Со(М)а D.
Определение 2. Выпуклым телом в банаховом пространстве X именуется выпуклое замкнутое множество, имеющее хоть одну внутреннюю точку.
Упражнение 4. Продемонстрируйте, что для множества М = = {0, хь х„}, где элементы xi, х„ образуют базис банахова пространства X, множество Со(тИ) есть выпуклым телом в X.
п
Указание. Удостоверьтесь в надежности, что точка х = -^ есть
внутренней точкой множества Со(М).
Подводя итог приведем усиленный вариант теоремы Броуэ- ра (подтверждение см. [11], стр. 573).
Теорема 2 (Броуэр). Пускай Q — выпуклое ограниченное тело n-мерного банахова пространства X. Тогда каждый постоянный оператор А, отображающий множество Q в себя, имеет в Q неподвижную точку.
35.2. Нелинейные в полной мере постоянные их аппроксимации и операторы. В § 20 мы изучали линейные в полной мере постоянные операторы. В этом пункте будут приведены нужные сведения о нелинейных в полной мере постоянных операторах.
Определение. Нелинейный оператор А с областью определения D(A)czX и с областью значений в У (X и Y — банаховы пространства) именуется в полной мере постоянным (на D(A)), если он постоянен на D(A) и переводит каждое ограниченное множество, лежащее в Ь(Л), в компактное в У множество.
Упражнение I. Продемонстрируйте, что любой постоянный оператор Л: X — У, где X и У — конечномерные банаховы пространства, есть в полной мере постоянным.
Упражнение 2. Пускай X, У, Z — банаховы пространства. Пускай оператор F: Х-*- У ограниченный и постоянный, а Л: У -Z— линейный в полной мере постоянный оператор (Л е Gfl(y,Z)). Докажите, что оператор AF — в полной мере постоянный.
Введем операторы Шаудера (нелинейные проекторы), аппроксимирующие нелинейный в полной мере постоянный оператор Л. Пускай оператор Л постоянен на ограниченном множестве
D а X и множество A(D)aY компактно. По критерию Хаус- дорфа (см. п. 19.3) для каждого е0 существует множество
Mz = {yt е A (D), i= 1, …. п),
являющееся конечной е-сетью множества A(D) — замыкания множества A(D). Разглядим оператор Аг, отображающий D в У и определяемый следующим правилом: для х е D
п
2 f1! (*) У,
Ае(х) = —«———— . (О
Z ^
г=1
где pt(x) = 0, в случае, если \\Ах — у,\\ е, и р,(х) = в — \\Ах — у,\\, в случае, если ЦАх — уЛ^е. Оператор Аг довольно часто именуют е-проектором Шаудера.
Упражнение 3. Докажите, что оператор Аг постоянен на D. Воспользуйтесь непрерывностью нормы.
Отметим сейчас кое-какие свойства оператора Ае. Свойство 1. || А (х) — Ае (х) е для всех х е D, т. е. оператор Ае аппроксимирует оператор Л на Л с точностью е. Вправду,
п п п
2 ц, (х) А (х) ? Цг (х) yt Yj ^г М 1А (*) — У А А[х)-АЛх) = ^-п = •
? (*) ? 1Ч (х) Z ^г М
i =1 i-l
Отсюда вытекает, что
|| Л (а) — А, (*) к ———— ,
i=-i
где суммирование в знаменатель и числитель ведется лишь по тем индексам i, для которых ||Лх — уМ
п
Е (*) е
||Л(х)-Ле(*)||
ЁМ*
г = 1
Тем самым свойство 1 доказано.
Замечание. При построении s-проектора Ле возможно вместо конечной е-сети множества A(D) забрать конечную e-сеть любого компактного множества, содержащего A{D).
Упражнение 4. Продемонстрируйте, что в полной мере постоянный оператор A: Dc.X-+Y (X и Y—банаховы пространства) возможно аппроксимировать е-проекторами на любом ограниченном множестве D\ cz D.
Подводя итог пункта сформулируем еще одно свойство е- проектора Шаудера Ае, доказать которое мы предлагаем читателю.
Свойство 2. Область значений оператора Аг содержится в Co(Mg), где Ме — конечная е-сеть множества A{D).
35.3. Принцип неподвижной точки Шаудера. Посредством теоремы Броуэра возможно обосновывать разные теоремы о неподвижных точках нелинейных операторов в бесконечномерных банаховых пространствах. В этом пункте будет доказан принцип неподвижной точки Шаудера.
Теорема (принцип Шаудера). Пускай оператор А отображает замкнутое ограниченное выпуклое множество D банахова пространства X в себя. Тогда, в случае, если А в полной мере постоянен на D, то он имеет на D неподвижную точку.
Подтверждение. Будем рассуждать от противного. Пускай оператор А не имеет на D неподвижных точек. Тогда найдется ео 0 такое, что для всех xeD
М(*)-*Цео. (1)
Вправду, в случае, если это не верно, то найдется последовательность {*п}с D такая, что
1М (*„)-*„ ||- 0, л-*оо. (2)