ЛЕКЦИЯ 1
машин и Теория механизмов (ТММ): объект изучения, главные понятия, задачи и цели. Главные характеристики механизмов: функции положений, первая и вторая передаточные функции, коэффициент нужного действия (КПД).
машин и Теория механизмов. Неспециализированные сведения
машин и Теория механизмов – раздел прикладной механики, в котором изучаются автомобили и входящие в их состав механизмы.
Машина – техническая совокупность, предназначенная для обеспечения усилий и осуществления движений, нужных для исполнения какого-либо технологического процесса. По функциональному назначению различают транспортные, технологические, энергетические и информационные автомобили.
- Транспортные автомобили предназначены для грузов и перемещения пассажиров в пространстве. К ним относятся машины, локомотивы, водный и воздушный транспорт, ракеты-носители, подъемно-транспортные автомобили; роботы-манипуляторы, предназначенные для исполнения транспортных операций.
- Технологические автомобили предназначены для заготовок и обработки материалов с целью получения готовых изделий. К технологическим автомобилям относится главное оборудование предприятий: металлообрабатывающие, деревообрабатывающие станки, прокатные станы, кузнечно-прессовые автомобили, автомобили литья под давлением и т.п.; роботы-манипуляторы, предназначенные для исполнения главных технологических операций (сварка, сборка, окраска).
- Энергетические автомобили предназначены для преобразования подаваемой к ним энергии одного вида в энергию другого вида, нужную для исполнения технологического процесса. К ним относятся генераторы и двигатели.
- Информационные автомобили предназначены для преобразования информации. К ним относятся электронные счётные автомобили разных правил действия, периферийное оборудование ЭВМ (принтеры, плоттеры, дигитайзеры, графопостроители, сканеры и т.п.).
Как сложные совокупности, автомобили складываются из следующих функциональных частей: механическая часть, двигатели, источники питания, совокупность управления перемещением. Механическая часть помогает для преобразования механической энергии двигателей в энергию требуемых перемещений рабочих органов автомобили. Механическая часть, в большинстве случаев, имеет несколько отдельных механизмов. Двигатели, по принципу действия, смогут быть тепловыми (к примеру, двигатели внутреннего сгорания), электрическими, гидравлическими либо пневматическими. Источники питания смогут быть как независимыми, так и стационарными. Совокупность управления перемещением осуществляет контроль внутреннего состояния автомобили, состояния и управляемых перемещений окружающей среды посредством датчиков, информация с которых подается на входы вычислительной совокупности, управляющей энергией источников питания автомобили. Современные автомобили, совокупности управления перемещением которых выстроены на базе микропроцессорных средств, образуют особенный класс автомобилей – мехатронные совокупности.
В ТММ изучаются теоретические базы строения, проектирования и функционирования механизмов и автомобилей, разрабатываются инженерные способы синтеза и анализа механизмов, каковые разрешают проектировать новые автомобили, отвечающие всему комплексу требований задания на проектирование (технических, эксплуатационных, экономических, эргономических, экологических).
Анализ любого сложного объекта пребывает в том, дабы распознать особенности и свойства объекта методом его расчленения на более простые составляющие. Под синтезом, напротив, подразумевается создание сложного объекта, владеющего заданными чертями, из некоего числа элементов с заблаговременно известными особенностями. В теории механизмов решаются задачи структурного, кинематического, динамического (силового), и точностного синтеза и анализа механизмов.
ЛЕКЦИЯ 2
Понятие кинематической классификация и пары кинематических пар. Условные кинематических пар и обозначения звеньев на схемах механизмов. Структурная и кинематическая схемы механизма. Классификация механизмов.
Классификация механизмов
Механизмы различаются по функциональному назначению, по конструктивному устройству, по размещению в пространстве, по наличию либо отсутствию замкнутых кинематических контуров.
По функциональному назначению механизмы подразделяются на аккуратные, передаточные и программные.
- Аккуратные механизмы предназначены для приведения в перемещение рабочих органов автомобили в соответствии с делаемым технологическим процессом.
- Передаточные механизмы помогают для преобразования механической энергии двигателей в механическую энергию с параметрами, требуемыми для приведения в перемещение входных звеньев аккуратного механизма.
- Программные механизмы задают программу перемещения механической части автомобили.
Пример
Разглядим транспортную машину – автомобиль. Рабочими органами автомобиля являются колеса. Аккуратный механизм – шасси. Коробка передач – многоступенчатый передаточный механизм, нужный для согласования работы двигателя и шасси в разных режимах перемещения автомобили. Двигатель автомобиля содержит газораспределительный механизм, что есть программным (он руководит перемещением впускных и выпускных клапанов двигателя).
По конструктивному устройству различают рычажные, зубчатые, кулачковые и фрикционные механизмы.
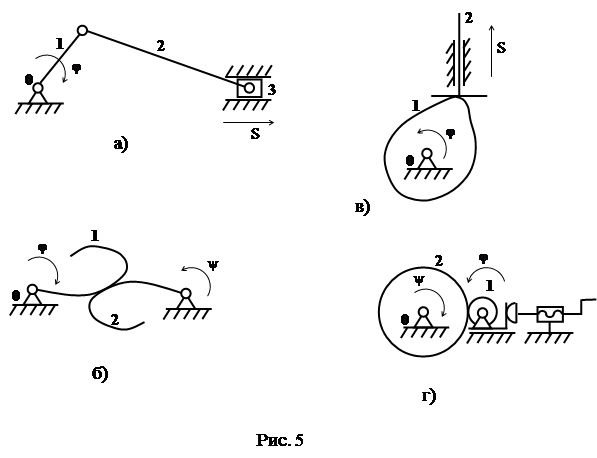
- Механизм, в котором все кинематические пары низшие, именуется рычажным (рис. 5,а).
- В зубчатом механизме перемещение от одного звена к второму передается при помощи зубчатого зацепления (рис. 5,б).
- Кулачковый механизм содержит звено со сложным профилем, именуемое кулачком (рис 5,в).
- Во фрикционном механизме перемещение от одного звена к второму передается за счет сил трения (рис. 5,г; звенья вспомогательного винтового механизма, предназначенного для поджатия колеса 1, не пронумерованы).
Механизмы также будут быть комбинированными: к примеру, зубчато-рычажный либо зубчато-фрикционный механизмы.
 |
По размещению в пространстве механизмы подразделяются на плоские и пространственные.
- Механизм именуется плоским, в случае, если траектории точек всех его подвижных звеньев находятся в плоскостях, параллельных неподвижной плоскости. На рис. 5 продемонстрированы структурные схемы плоских механизмов.
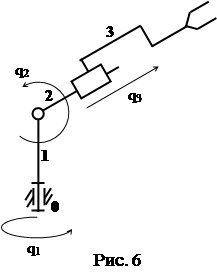
- Механизм именуется пространственным, в случае, если траектории точек его подвижных звеньев лежат в непараллельных плоскостях. На рис. 6 приведена схема пространственного механизма – манипулятора, трудящегося в сферической совокупности координат.
 |
Механизм именуется замкнутым, в случае, если каждое его звено образует, как минимум, две кинематические пары. В случае, если имеется хотя бы одно звено, образующее лишь одну кинематическую несколько, механизм – разомкнутый.
Механизм именуется одноконтурным, если он содержит один замкнутый кинематический контур. В случае, если в механизме имеется более чем один замкнутый контур, то механизм – многоконтурный. На рис. 5 приведены схемы замкнутых одноконтурных механизмов; на рис. 6 – схема разомкнутого механизма, не имеющего замкнутых кинематических контуров.
Контрольные вопросы
1. Что именуется кинематической парой?
2. Что именуют подвижностями кинематической пары?
3. Как определяется класс кинематической пары?
4. Может ли кинематическая пара иметь класс выше пятого? Обоснуйте собственный ответ.
5. Какие конкретно кинематические пары именуются низшими? Высшими?
6. Чем отличается структурная схема механизма от его кинематической схемы?
7. Перечислите разновидности механизмов по функциональному назначению.
8. Какие конкретно механизмы именуются рычажными?
9. Чем отличается плоский механизм от пространственного механизма?
10. Сформулируйте условие, в соответствии с которым механизм определяется как замкнутый.
11. Может ли разомкнутый механизм иметь замкнутые кинематические контуры? Обоснуйте собственный ответ.
ЛЕКЦИЯ 3
Плоские четырехзвенные рычажные механизмы. Наименования звеньев рычажных механизмов. Степени свободы механизмов. Универсальные структурные формулы. Главные и местные подвижности в механизмах.
Местные подвижности
Местными подвижностями именуются степени свободы механизма, не оказывающие влияния на передачу главного перемещения.
Разглядим механизм (Рис. 9). По формуле Сомова – Малышева число его степеней свободы ( , , )
.
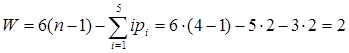Другими словами, данный механизм не только существует как пространственный, но еще имеет две степени свободы. Одна степень свободы тут есть главной подвижностью, нужной для передачи перемещения от звена 1 к звену 3. Вторая степень свободы (вращение шатуна 2 около собственной оси) не воздействует на передачу главного перемещения, исходя из этого есть местной подвижностью.
В общем случае, механизм может иметь как главные, так и местные подвижности: его число степеней свободы определяется равенством:
,
где WO – число главных, WМ – число местных подвижностей.
Местные подвижности довольно часто предусматривают в механизмах для обеспечения более благоприятного распределения нагрузки на звенья и равномерного изнашивания контактирующих поверхностей. При необходимости, местные подвижности возможно устранить, повысив класс соответствующих кинематических пар.
Контрольные вопросы
1. Перечислите чаще всего применяемые плоские четырехзвенные рычажные механизмы. Приведите примеры автомобилей либо устройств, в которых имеется такие механизмы.
2. Чем отличается кривошип от коромысла? Коромысло от кулисы?
3. Что именуют степенью свободы механизма?
4. Чем отличается механизм от конструкции?
5. Что свидетельствует множитель «6» в структурной формуле Сомова — Малышева?
6. Для каких механизмов употребляется структурная формула Чебышева?
7. Какие конкретно механизмы именуют клиновыми? Какую структурную формулу направляться применять для расчета степеней свободы клинового механизма?
8. Что именуют местной подвижностью?
9. С какой целью местные подвижности предусматривают в механизмах?
10. Как возможно устранить местную подвижность?
ЛЕКЦИЯ 4
Избыточные связи в механизмах. Классификация, устранение и выявление избыточных связей. Принцип строения рычажных механизмов. Классификация структурных групп.
Избыточные связи
Избыточными именуют такие связи, каковые не накладывают новых ограничений на перемещения звеньев механизма, а лишь повторяют уже существующие. Избыточные связи смогут быть как в отдельных кинематических парах, так и на уровне механизма в целом. Различают избыточные связи трех типов: А, Б и В (по предложению доктора наук Озола).
Избыточные связи типа А имеют место в отдельных кинематических парах. Для передачи упрочнения от одного звена к второму теоретически достаточно контакта в одной точке (Рис. 10,а). В случае, если передача упрочнения обеспечивается поверхностным контактом, то соприкосновение звеньев во всех точках поверхности, не считая одной, будет образовывать избыточные связи типа А (Рис. 10,б).
 |
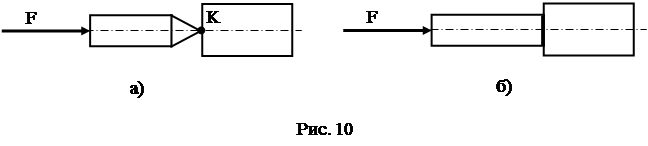Избыточные связи типа А являются нужными, в то время, когда требуется передача больших упрочнений, потому, что звенья настоящих механизмов не являются полностью жёсткими, и при точечного контакта при большой силовой нагрузке будут иметь место значительные деформации, допустимо кроме этого разрушение звеньев в зоне их соприкосновения. В отдельных случаях связи типа А являются вредными и устраняются. К примеру, кинематическая пара цилиндр-поршень в двигателе внутреннего сгорания будет работоспособной, в случае, если поверхностный контакт поршня с цилиндром заменить линейным контактом цилиндра с компрессионными кольцами (Рис. 11).
 |
Избыточные связи типа Б имеют место в кинематических парах с ветвлением. Число избыточных связей типа Б рассчитывается по формуле:
,
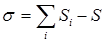где i — индекс ветвления пары, Si – число свободных связей в i – той ветви, S – класс кинематической пары.
Пример
На рис. 12 изображена поступательная кинематическая пара с двумя ветвлениями.
 |
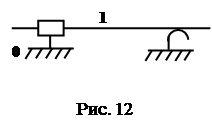Вычислим число избыточных связей типа Б: , (ветвление поступательное), (ветвление цилиндр-плоскость) (класс поступательной пары – пятый),
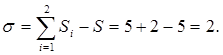
Избыточные связи типа Б увеличивают жесткость кинематической пары, но требуют повышенной точности сборки и изготовления звеньев пары.
Избыточные связи типа В образуются при замыкании кинематических цепей в контуры, из этого их второе наименование – контурные избыточные связи. Их число определяется по формуле Озола:
,
где W – число степеней свободы механизма, k – число замкнутых кинематических контуров, f – суммарное число степеней свободы кинематических пар механизма. Для плоского механизма число контурных избыточных связей возможно кроме этого отыскано по формуле Малышева:
,
где WЧ – число степеней свободы механизма, вычисленное по формуле Чебышева, WСМ – число степеней свободы того же механизма, вычисленное по формуле Сомова – Малышева.
Задача
Выяснить число избыточных связей в плоском шарнирном четырехзвенном механизме (Рис. 7,а).
Ответ
Для данного механизма , (один замкнутый контур) и (четыре одноподвижные кинематические пары). Тогда по формуле Озола:
.
Механизм имеет три контурные избыточные связи, что и было отмечено в Задаче 2 п. 3.2.
Контурные избыточные связи увеличивают жесткость механизма, но требуют повышенной точности сборки механизма и изготовления звеньев. При необходимости, они смогут быть устранены методом понижения класса одной либо нескольких кинематических пар.
Избыточные связи смогут быть кроме этого привнесены в механизм методом введения в его схему дополнительных звеньев. Разглядим механизм сдвоенного параллелограмма (рис. 13).
 |
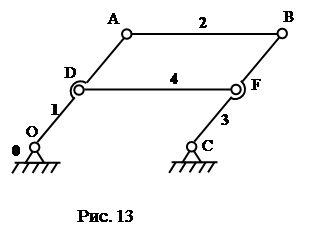Тут дополнительное звено – шатун 4. Так как механизм плоский, вычислим его число степеней свободы по формуле Чебышева ( , ):
.
Полученный итог свидетельствует, что с позиций структурного строения, разглядываемая совокупность механизмом не есть. Чтобы появилась одна степень свободы, требуется соблюдение геометрических условий: , , , . Следовательно, введение дополнительных звеньев в схему механизма влечет за собой необходимость правильного соблюдения определенных геометрических размеров при изготовлении звеньев.
ЛЕКЦИЯ 5
порядок и Структурный анализ механизма его исполнения. Принцип образования рычажных механизмов. Структурные модификации механизма. Синтез структурных модификаций. Кинематический анализ механизма. Графические и аналитические способы кинематического анализа: преимущества и недочёты.
ЛЕКЦИЯ 6
Графический и аналитический способы определения функции положения механизма. Способы графического дифференцирования.
ЛЕКЦИЯ 7
Теоретические базы способа векторных замыслов. Вычисление ускорений и скоростей звеньев плоского механизма способом векторных замыслов. Применение понятий мгновенного мгновенного центра и центра скоростей ускорений в ответе задач кинематического анализа плоских механизмов.
7.1. Способ векторных замыслов
Кое-какие физические размеры, характеризующие состояние исследуемой совокупности, смогут быть математически представлены в виде направленных отрезков (векторов). К примеру, векторными размерами являются скорости и ускорения точек механической совокупности, силы, приложенные к совокупности, переменные напряжение и ток в электрической цепи и т.п. В аналогичных случаях процессы, протекающие в совокупности, описываются векторными уравнениями. В случае, если векторы, входящие в уравнения, находятся в одной и той же плоскости, то уравнения смогут быть решены методом геометрических построений векторов на плоскости в заблаговременно принятом масштабе. В этом содержится мысль способа векторных замыслов. В то время, когда требуется вычислить ускорения и скорости звеньев плоского механизма в каких-либо его положениях, способ векторных замыслов есть эргономичным и довольно часто используется на практике.
Как мы знаем из теоретической механики, ускорение и скорость любой точки жёсткого тела, совершающего плоское перемещение (Рис. 27), смогут быть отысканы посредством векторных уравнений:
, ,
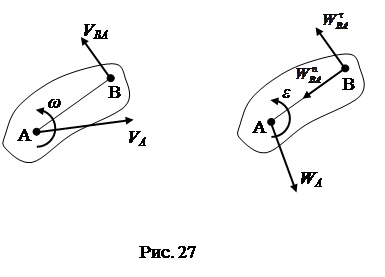
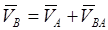где — векторы полных ускорения и скорости точки А тела, — вектор скорости точки B относительно точки A, — векторы обычного и тангенциального (касательного) ускорений точки B относительно точки A. Модули векторов , вычисляются по формулам
, , ,
где ?, ? – угловые ускорение и скорость тела.
Векторные замыслы, соответствующие векторным уравнениям ускорений и скоростей, представлены на рис. 28.
 |
Так, сделав графически сложение векторов и измерив на замыслах отрезки, соответствующие скорости и ускорению , приобретаем данные о величинах и направлениях векторов и .
Задача
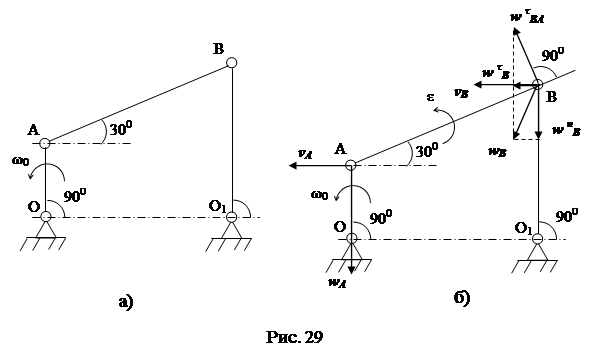Стержень OA шарнирного четырехзвенного механизма (рис. 29,а) вращается с постоянной угловой скоростью ?0. Выяснить угловую скорость, угловое ускорение стержня AB, и ускорение шарнира B в положении, указанном на рисунке, в случае, если AB = 2OA = 2a.
Ответ
Стержень AB изображенного на рисунке четырехзвенного механизма совершает плоское перемещение, а стержни OA и O1B вращаются около неподвижных центров O и O1. Отыщем скорость шарнира A:
.
Вектор перпендикулярен OA и направлен в рис вращения и сторону (стержня. 18). Для скорости шарнира B справедливо равенство:
,
причем направление , в соответствии с положению механизма, будет то же, что и у . Из этого направляться, что , , , т.е. стержень AB совершает мгновенно-поступательное перемещение.
Отыщем ускорение шарнира A. Так как данный шарнир движется около неподвижной точки O, то для его ускорения справедливо равенство:
,
где — обычное ускорение, направленное от точки A к центру вращения O; , т.к. . В этом случае . Для ускорения шарнира B справедливо равенство:
,
где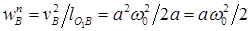 
— обычное ускорение шарнира B в его перемещении около неподвижной точки O1; — обычное ускорение шарнира B относительно точки A.
 |
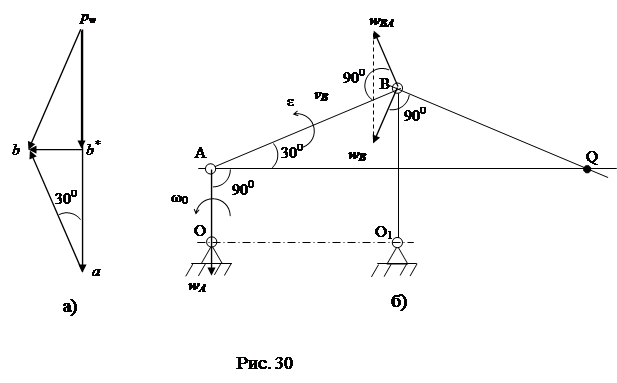Малоизвестные по величине векторы определим, выстроив замысел ускорений. Для этого из произвольной точки pw, именуемой полюсом замысла ускорений, отложим отрезок pwa,, отображающий ускорение (рис. 30,а). Тогда, проводя через прямую и точку, перпендикулярную AB, возьмём направление тангенциального ускорения .
Составляющую результирующего ускорения отложим из полюса pw в виде отрезка pwb*, протяженность которого в два раза меньше pwa. Замкнем замысел ускорений прямой, перпендикулярной стержню O1B и задающей направление . На пересечении двух перпендикуляров возьмём точку b. Отрезок pwb будет отображать ускорение шарнира B, а отрезок ab – ускорение . Замысел ускорений графически отображает векторное равенство, из замысла легко определяются все малоизвестные ускорения:
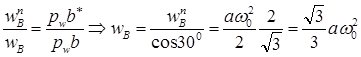— ускорение шарнира B;
, 
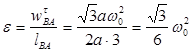— угловое ускорение стержня AB. Направления всех вычисленных ускорений и скоростей точек механизма изображены на рис. 29,б.
ЛЕКЦИЯ 1
машин и Теория механизмов (ТММ): объект изучения, главные понятия, задачи и цели. Главные характеристики механизмов: функции положений, первая и вторая передаточные функции, коэффициент нужного действия (КПД).
машин и Теория механизмов. Неспециализированные сведения
машин и Теория механизмов – раздел прикладной механики, в котором изучаются автомобили и входящие в их состав механизмы.
Машина – техническая совокупность, предназначенная для обеспечения усилий и осуществления движений, нужных для исполнения какого-либо технологического процесса. По функциональному назначению различают транспортные, технологические, энергетические и информационные автомобили.
- Транспортные автомобили предназначены для грузов и перемещения пассажиров в пространстве. К ним относятся машины, локомотивы, водный и воздушный транспорт, ракеты-носители, подъемно-транспортные автомобили; роботы-манипуляторы, предназначенные для исполнения транспортных операций.
- Технологические автомобили предназначены для заготовок и обработки материалов с целью получения готовых изделий. К технологическим автомобилям относится главное оборудование предприятий: металлообрабатывающие, деревообрабатывающие станки, прокатные станы, кузнечно-прессовые автомобили, автомобили литья под давлением и т.п.; роботы-манипуляторы, предназначенные для исполнения главных технологических операций (сварка, сборка, окраска).
- Энергетические автомобили предназначены для преобразования подаваемой к ним энергии одного вида в энергию другого вида, нужную для исполнения технологического процесса. К ним относятся генераторы и двигатели.
- Информационные автомобили предназначены для преобразования информации. К ним относятся электронные счётные автомобили разных правил действия, периферийное оборудование ЭВМ (принтеры, плоттеры, дигитайзеры, графопостроители, сканеры и т.п.).
Как сложные совокупности, автомобили складываются из следующих функциональных частей: механическая часть, двигатели, источники питания, совокупность управления перемещением. Механическая часть помогает для преобразования механической энергии двигателей в энергию требуемых перемещений рабочих органов автомобили. Механическая часть, в большинстве случаев, имеет несколько отдельных механизмов. Двигатели, по принципу действия, смогут быть тепловыми (к примеру, двигатели внутреннего сгорания), электрическими, гидравлическими либо пневматическими. Источники питания смогут быть как независимыми, так и стационарными. Совокупность управления перемещением осуществляет контроль внутреннего состояния автомобили, состояния и управляемых перемещений окружающей среды посредством датчиков, информация с которых подается на входы вычислительной совокупности, управляющей энергией источников питания автомобили. Современные автомобили, совокупности управления перемещением которых выстроены на базе микропроцессорных средств, образуют особенный класс автомобилей – мехатронные совокупности.
В ТММ изучаются теоретические базы строения, проектирования и функционирования механизмов и автомобилей, разрабатываются инженерные способы синтеза и анализа механизмов, каковые разрешают проектировать новые автомобили, отвечающие всему комплексу требований задания на проектирование (технических, эксплуатационных, экономических, эргономических, экологических).
Анализ любого сложного объекта пребывает в том, дабы распознать особенности и свойства объекта методом его расчленения на более простые составляющие. Под синтезом, напротив, подразумевается создание сложного объекта, владеющего заданными чертями, из некоего числа элементов с заблаговременно известными особенностями. В теории механизмов решаются задачи структурного, кинематического, динамического (силового), и точностного синтеза и анализа механизмов.