Совокупность m линейных уравнений с n переменными (неспециализированный вид). Матрица совокупности. Матричная форма записи совокупности линейных уравнений. Совместные (определенные и неизвестные) и несовместные совокупности. Теорема Крамера о разрешимости совокупности n линейных уравнений с n переменными. Ответ таковой совокупности: а) по формулам Крамера; б) способом обратной матрицы; в) способом Гаусса. Понятие о способе Жордана-Гаусса. Теорема Кронекера-Капелли. неопределённости и Условие определённости любой совместной совокупности линейных уравнений. Базовые (главные) и свободные (неосновные) переменные. Базовое ответ. Совокупность линейных однородных ее решения и уравнений. Понятие о модели Леонтьева. ([1либо 6, § 2.1 – 2.7]; [2 либо 7, § 2.1, 2.5], либо [3, § 2.1 – 2.8], либо [4, § 2.1 – 2.8]).
При изучении материала темы направляться освоить матричную форму записи заданной совокупности n линейных уравнений с n переменными и мочь переходить к данной форме от общего вида совокупности и напротив. Нужно знать и мочь растолковать, какие конкретно совокупности уравнений именуются совместными (определенными и неизвестными) и несовместными. Нужно твердо уяснить, что вопрос о разрешимости совокупности n линейных уравнений с n переменными устанавливается посредством теоремы Крамера ([1, либо 6, либо 3, § 2.2]). Решаются же такие совокупности разными методами: по формулам Крамера, посредством обратной матрицы и способом Гаусса. Самый серьёзен для практики способ Гаусса, имеющий по сравнению с другими методами ответа последовательность преимуществ: он менее трудоемок, разрешает конкретно установить, есть ли эта совокупность определенной, неизвестной либо несовместной, а при совместности совокупности – выяснить число ее линейно свободных уравнений и исключить «лишние».
Способ Жордана–Гаусса [2 либо 7, § 2.3, пример 2.49] либо [3, § 2.8, пример 2.44] разрешает стремительнее, чем хороший, решать совокупность уравнений и потому пользуется спросом в прикладных математических направлениях. Наряду с этим направляться иметь в виду, что в настоящих прикладных задачах совокупности уравнений с большим числом уравнений и переменных решаются посредством пакетов прикладных программ, к примеру, Excel, MathCAD и др.
Практический интерес в приложениях воображает случай, в то время, когда число m уравнений совокупности меньше числа n переменных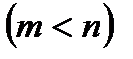 
. Рассмотрение таких совокупностей ведет к разбиению переменных на базовые (главные) и свободные (неосновные) переменные и выделению из общего количества ответов совокупности базовых ответов, в которых все свободные (неосновные) переменные равны нулю.
В соответствии с теореме Кронекера – семь дней совокупность линейных уравнений совместна тогда и лишь тогда, в то время, когда ранг матрицы совокупности А равен рангу расширенной матрицы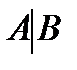 
, т.е. 
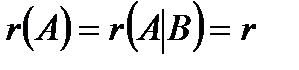. Наряду с этим, в случае, если 
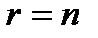(n – число переменных), то совокупность определенная, в случае, если 
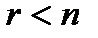– неизвестная и имеет нескончаемое множество ответов.
Для решения совокупности m линейных уравнений с n переменными 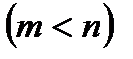вовсе не нужно обнаружить намерено ранги 
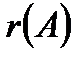и 
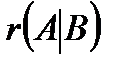, а достаточно применить способ Гаусса. В случае, если хотя бы одно из уравнений совокупности на «прямом ходе» способа Гаусса приводится к виду 
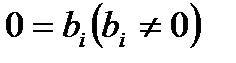, то совокупность несовместная, в случае, если к виду 0=0, то совокупность совместная и неизвестная. В последнем случае уравнения вида 0=0 исключаются из совокупности, а члены уравнения с 
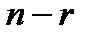свободными переменными переносятся в правые части уравнений. Потом, применяя «обратный движение» способа Гаусса, приобретают выражения r базовых переменных через 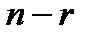свободных, т.е. неспециализированное ответ совокупности (см. [1 либо 6, пример 2.4], [2 либо 7, пример 2.36] либо [3, примеры 2.4, 2.44]).
направляться иметь ввиду, что неспециализированное число ответов совместной совокупности линейных уравнений вечно, тогда как число ее базовых ответов само собой разумеется и не превосходит числа сочетаний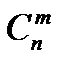 
(а правильнее 
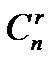, где r – ранг матрицы совокупности).
Изюминкой разглядываемых потом совокупностей однородных уравнений есть то, что они в любой момент совместны, поскольку имеют, по крайней мере, нулевое ответ (0, 0, …, 0). Ненулевое ответ такие совокупности имеют лишь тогда, в то время, когда ранг матрицы совокупности меньше числа переменных, т.е.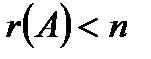 
, либо, что то же самое, в то время, когда определитель матрицы А равен нулю: 
.
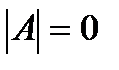направляться подчернуть, что матричное уравнение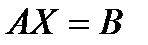 
, к которому сводится совокупность линейных уравнений (А – матрица совокупности, Х – малоизвестный столбец переменных, В – столбец свободных участников) может рассматриваться и при, в то время, когда Х – малоизвестная матрица. По большому счету матричные уравнения несложного вида с малоизвестной матрицей Х имеют вид 
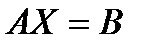(1), 
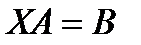(2), 
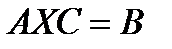(3), где А, В, С, Х – матрицы таких размеров, что все применяемые операции вероятны, а правые и левые части этих матричных уравнений воображают матрицы однообразных размеров.
Решения матричных уравнений (1) и (2) соответственно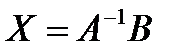 
и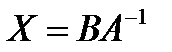 
(в случае, если А – квадратная матрица, 
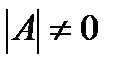), а матричного уравнения (3) 
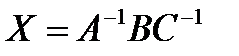(в случае, если А и С – квадратные матрицы и , 
).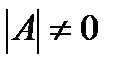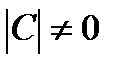