2.1. математическая модель и Постановка задачи транспортной задачи. Предположим, что существуют N потребителей и M поставщиков некоего однородного груза, у каждого из поставщиков определенный запас этого груза (Ai единиц, i=1,2,…,M), а каждому из потребителей требуется Bj единиц груза (j=1,2,…, N). Известны кроме этого затраты cij на перевозку единицы груза от поставщика Ai к потребителю Bj. Требуется разработать таковой замысел перевозок от поставщиков к потребителям, дабы суммарные затраты на перевозки были минимальными (наряду с этим должны быть по возможности вывезены все запасы поставщиков и удовлетворены все запросы потребителей).
При, в то время, когда суммарные запасы совпадают с суммарными запросами, задача именуется задачей с верным балансом, а ее модель — закрытой. В другом случае говорят о задаче с неправильным балансом и об открытой модели. Существуют особые приемы приведения открытой модели к закрытой (они будут рассмотрены позднее).
Эти транспортной задачи в большинстве случаев записываются в виде таблицы, заголовки строчков которой содержат данные о запасах, заголовки столбцов – данные о запросах, а в нижнем правом углу каждой ячейки указывается цена перевозки единицы груза (затраты на перевозку единицы груза).
При составлении математической модели через xij обозначается количество единиц груза, что будет перевезен от поставщика Ai к потребителю Bj (количество перевозок от Ai к Bj). Эти значения будут вноситься в центр соответствующей ячейки.
С учетом сообщённого целевая функция принимает вид
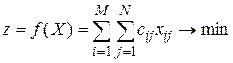
(просуммированы все произведения затрат на соответствующий количество перевозок). Ограничения связаны с удовлетворением запросов и вывозом запасов, исходя из этого математическая модель имеет форму:
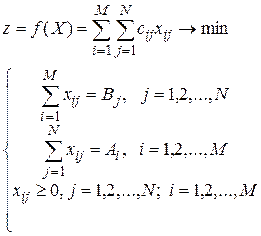
| Пример 2.1. Транспортная задача задана посредством таблицы 2.1, из которой видно, что на складах трех поставщиков A1, A2, A3 сосредоточены соответственно 30, 190 и 250 единиц груза, потребители B1, B2, B3, B4 нуждаются соответственно в 70, 120, 150, 130 единицах груза, а стоимости перевозок указаны конкретно в таблице. |
| В А | ||||
Таблица 2.1.
Увидим, что суммарные запасы (30+190+250=470) равны суммарным запросам (70+120+150+130=470). Разместим в главной (незаштрихованной) части таблицы искомые количества перевозок xij и перейдем к составлению математической модели. Увидим, что нумерация соответствует привычной нумерации элементов в матрицах (i – номер строчка, j – номер столбца). Итак, целевая функция принимает вид
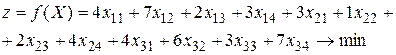 (2.1)
(2.1)
(просуммировали произведения цен на количества перевозок по всем строчкам). При построении совокупности ограничений сперва суммируем количества перевозок по каждому столбцу (удовлетворяем все запросы), а позже суммируем количества перевозок по каждой строке (вывозим все запасы). Учтем кроме этого неотрицательность значений xij и приобретаем следующие условия:
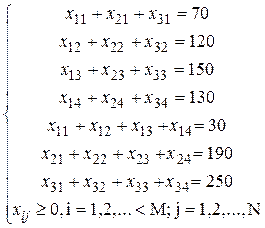 (2.2)
(2.2)
Итак, мы выстроили математическую модель предложенной задачи с целевой функцией (2.1) и совокупностью ограничений (2.2).
Транспортная задача сводится к задаче линейного программирования, но для ее ответы существуют особые методы. Наряду с этим сперва задача сводится к закрытой, после этого строится начальное ответ, а после этого оно оптимизируется посредством способа потенциалов.
2.2. Построение начального опорного ответа. Разглядим два главных приема для задач с верным балансом. Первый из них имеет более несложный метод, а второй дает ответ, более близкое к оптимальному.
Способ северо-западного угла. Главная мысль содержится в том, вычисление значений xij начинается с верхней левой клетки (северо-западный угол таблицы). Из запросов и значений запасов, ей соответствующих (A1 и B1) выбираем минимальное – это и будет количество перевозок x11. Наряду с этим или удовлетворены все запросы (и тогда из рассмотрения исключается потребитель, наряду с этим в таблице в оставшихся ячейках соответствующего столбца ставятся прочерки, а количество запасов в соответствующей строчке значительно уменьшается на это значение), или вывезены все запасы (из рассмотрения исключается поставщик, прочерки ставятся в строчке и значительно уменьшается количество запросов). При, в то время, когда A1=B1, вычеркивается или строчок, или столбец (но не столбец и строка в один момент!) Потом действия повторяются со следующей ячейкой, которая была верхней левой – и без того до момента, пока не окажется, что все запасы вывезены, а все запросы удовлетворены. Наряду с этим клетки, в каковые попали значения xij,, именуются занятыми.
Внимание!Чтобы не было неточностей нужно убедиться в том, что число занятых клеток равняется M+N-1; в другом случае выстроенное начальное ответ не будет опорным. Наряду с этим нужно не забывать, что, в силу сформулированного правила выбора количества перевозок, в занятых клетках могут быть значения, равные нулю!
Пример 2.2. Ниже в таблицах 2.2-2.7 приводится пошаговое построение способом северо-западного угла начального опорного ответа для закрытой задачи из примера 2.1; количества перевозок внесены в таблицы жирным курсивным шрифтом.
| В А | ||||
| — | — | — | ||
Таблица 2.2.
Таблица 2.3.
Таблица 2.4.
Таблица 2.5
| В А | ||||
| — | — | — | ||
| — | ||||
| — | — |
Таблица 2.6.
Таблица 2.7.
Итак, заняты 6 ячеек: (1;1), (2;1), (2;2), (2;3), (3;3) и (3;4) (тут, как и везде потом, в «адресе» ячейки первым указан номер строчка, вторым – номер столбца, заголовки в нумерации не учитываются). Количество занятых ячеек сходится с числом M+N-1=3+4-1=6. Мы выстроили начальное опорное ответ X1, остается определить значение целевой функции для этого опорного ответа (в свободных клетках, т.е. клетках с прочерками, значение количества перевозок считается равным нулю и потому на итог вычисления не воздействует): .
Способ минимальной цене. Главная мысль этого подхода — последовательная расстановка количеств перевозок в клетки с мельчайшей ценой среди незаполненных. При, в то время, когда имеется пара клеток с однообразной ценой, первой рассматривается та, в которую возможно записать громаднейший количество перевозок. Правило выбора значения из соответствующих запроса и запаса сохраняется, как сохраняется и необходимое количество занятых строчков, и возможность появления в занятой клетке нулевого значения.
Пример 2.3. В таблицах 2.8-2.13 приводится пошаговое построение начального опорного ответа способом минимальной цене для закрытой задачи из примера 2.1. Обратите внимание, что первый выбор сделать легко, а в таблице 2.8 видно, что в ячейках (2;3) и (1;3) однообразная цена затрат (равная 2). Потому, что в ячейку (2;3) возможно записать количество перевозок, равный 70, а в ячейку (1;3) – равный 30, выбираем ячейку с громадным количеством, т.е. (2;3) – см. таблицу 2.9.
| В А | ||||
| — | ||||
| — |
Таблица 2.8.
Таблица 2.9.
| В А | ||||
| — | — | — | ||
| — | — | |||
| — |
Таблица 2.10.
Таблица 2.11
| В А | ||||
| — | — | — | ||
| — | — | |||
| — |
Таблица 2.12.
Таблица 2.13
В итоге, как и положено, выстроенному начальному опорному ответу X2 соответствуют 6 занятых клеток. Наряду с этим значение целевой функции меньше, чем отысканное в примере 2.2, т.е. ответ X2 ближе к оптимальному.
Открытую модель нужно сперва свести к закрытой, для чего вводится фиктивный поставщик (с запасами, равными разности между запросами и запасами) либо фиктивный потребитель (с подобно определяемыми запросами). Стоимости перевозок в соответствующих строке либо столбце равны нулю, но в способе минимальной цене они учитываются в последнюю очередь. В ответе фиктивная строчок (столбец) не учитывается.
| Пример 2.4. Для предложенной транспортной задачи (таблица 2.14) составить начальные опорные ответы способами северо-минимальной стоимости и западного угла и сравнить значения целевой функции. |
| В А | |||
| Таблица 2.14 |
Ответ. В первую очередь, разумеется, что суммарные запасы равны 100, а суммарные запросы – 90. Исходя из этого нужно ввести фиктивного потребителя, запросы которого равны 10 (это дополнительный столбец, значения цен в котором будут равны 0) – см. таблицу 2.15, с которой начнем построение начального ответа способом северо-западного угла. На первом шаге для ячейки (1;1) запросов и значения запасов однообразны и равны 30, исходя из этого количества перевозок равен 30, вычеркиваем, к примеру, строчок (наряду с этим запросы в соответствующем столбце становятся равными 0). На следующем шаге (см. таблицу 2.16) в ячейку (2;1) ставится значение количества перевозок 0 – как минимальное из чисел 0 и 20, наряду с этим вычеркивается первый столбец.
| В А | |||
| — | — | ||
Таблица 2.15.
Таблица 2.16.
Таблица 2.17.
Таблица 2.18.
Таблица 2.19.
Совершим сейчас построение начального опорного ответа способом минимальной цене (таблицы 2.20-2.24).
| В А | |||
| — | — | ||
Таблица 2.20.
Таблица 2.21.
Таблица 2.22.
Таблица 2.23.
Таблица 2.24.
Замечание. При записи ответа (начального опорного ответа) последние столбцы в таблицах 2.19 и 2.24 не учитываются.
2.3. Проверка оптимальности ответа. Способ потенциалов.Для проверки оптимальности ответа введем потенциалы строчков (ui, i=1,2,…,M) и столбцов (vj, j=1,2,…,N) – числа, каковые определяются совокупностью уравнений , составленных по занятым клеткам. Увидим, что занятых клеток M+N-1, исходя из этого мы имеем совокупность из M+N-1 уравнений с M+N малоизвестными потенциалами. Это неизвестная совокупность, нас интересует любое частное ответ, исходя из этого любому из потенциалов возможно на первом шаге дать значение, равное нулю. Потом последовательно находятся все потенциалы, каковые записываются в дополнительный правый столбец и в дополнительную нижнюю строчок таблицы транспортной задачи (неспециализированную схему см. в таблице 2.25).
| B A | B1 | B2 | … | BM | Потенциалы строчков |
| A1 | с11 | с12 | … | с1N | u1 |
| A2 | с21 | с22 | … | с2N | u2 |
| … | … | … | … | … | … |
| AM | сM1 | сM2 | cMN | uM | |
| Потенциалы столбцов | v1 | v2 | … | vN |
Таблица 2.25
По окончании определения потенциалов находим оценки для свободных клеток по правилу , записываем их в верхнюю часть каждой свободной клетки. Ответ есть оптимальным, в случае, если все отысканные оценки неположительны (меньше либо равны 0).
Пример 2.5.Проверить оптимальность ответа, выстроенного в примере 2.4 (см. таблицу 2.24).
Ответ. Сперва по таблице 2.24 определяем потенциалы.
Занятыми являются клетки (1;1), (2;1), (2;2), (2;3), (3;2). С учетом цен, записанных в этих клетках, составляем совокупность уравнений 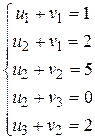
|
| В А | ui | |||
| — | — | |||
| — | — | -2 | ||
| vj | -1 |
Таблица 2.26.
Пускай . Потом последовательно: из первого уравнения , из второго уравнения , из третьего , из четвертого , из пятого . Результаты собраны в таблице 2.26.
Расчет оценок проводится по формуле конкретно в таблице 2.27, с учетом отысканных выше потенциалов
| В А | ui | |||
| 0+4-3=10 — | 0+(-1)-0=-1 | |||
| -2+1-4=-5 | -2+(-1)-0=-3 | -2 | ||
| vj | -1 |
Таблица 2.27.
Итак, видно, что в ячейке (1;2) оценка хороша, т.е. предложенное ответ не есть оптимальным.
2.4. Оптимизация ответа. Одним из главных понятий в этом пункте есть цикл – последовательность клеток таблицы транспортной задачи, в которой две и лишь две соседние клетки находятся в одной строке либо в одном столбце, причем первая и последняя клетки кроме этого находятся в одной строке либо в одном столбце. Как мы знаем, что в таблице транспортной задачи, содержащей опорное ответ, для любой свободной клетки возможно выстроить единственный цикл, содержащий часть и эту клетку занятых.
В случае, если ответ не оптимальное, то среди хороших оценок выбираем громаднейшую (при равенства громаднейших оценок – выбираем ячейку с мельчайшей ценой). Для выбранной ячейки строим цикл, включающий часть и эту клетку занятых клеток, причем свободная клетка приобретает символ «+», а потом символ чередуется. Для попавших в цикл ячеек определяем величину .Перемещаем перевозки по циклу в соответствии с правилом: в ячейках со знаком «+» q добавляется к значению xij, а в ячейках со знаком «-»q из xij вычитается. Наряду с этим клетка, в которой изначально был количество перевозок, равный q, делается безлюдной, а свободная с выбранной «нехорошей» оценкой — занятой.
Замечание. В случае, если минимальное значение q достигается в нескольких клетках, то лишь одна из них делается безлюдной, а в остальных количество перевозок выставляется равным 0; это разрешает сохранить нужное количество занятых клеток.
По окончании перемещения груза по циклу новое ответ проверяется на оптимальность, и при необходимости процесс повторяется.
Пример 2.6. Отыскать оптимальное ответ для транспортной задачи из примера 2.4.
Ответ.Условия были приведены в таблице 2.14. Задача была открытой, исходя из этого сперва был введен фиктивный потребитель. Начальное опорное ответ, выстроенное способом минимальной цене – в таблице 2.24. Таблица 2.27 (с оценками и потенциалами) свидетельствует, что выстроенное ответ не оптимальное, а ячейка (1;2) – единственная ячейка с хорошей оценкой. С нее и начнем строить цикл. По таблице 2.27 видно, что его образуют ячейки (1;2), (2;2), (2;1), (1;1). В силу вышесказанного ячейки
| В А | |||
| — | |||
| — | |||
| — | — |
Таблица 2.28.
Удостоверимся в надежности оптимальность этого замысла. По занятым клеткам составим совокупность уравнений для определения потенциалов и решим ее, полагая (читатель может выполнить это самостоятельно). После этого запишем потенциалы (см. таблицу 2.29) и в данной же таблице высчитаем оценки свободных клеток.
| В А | ui | |||
| 0+(-1)-0 | ||||
| 1+3-5 | ||||
| -1+1-4 | -1+(-1)-0 | -1 | ||
| vj | -1 |
Таблица 2.29.
Все оценки отрицательны, значит, отысканное опорное ответ есть оптимальным. Для завершения ответа отбрасываем столбец с фиктивным
| В А | ||
| — | ||
| — |
Таблица 2.30.
Увидим, что на втором складе осталось 10 единиц продукции, но это связано с тем, что задача была открытой.
2.5. Метод полного ответа транспортной задачи. Подводя результат вышесказанному, определим порядок действий при ответе транспортной задачи с M поставщиками и N потребителями.
1) Выяснить, есть ли задача закрытой либо открытой; в последнем случае ввести фиктивного потребителя либо поставщика и выстроить новую таблицу.
2) Выстроить начальное опорное ответ X1 (рекомендуется способ минимальной цене) и убедиться, что занято нужное число клеток (M+N-1) – см. п.2.2.
3) Отыскать потенциалы посредством занятых клеток из неизвестной совокупности ((i;j) – адреса занятых клеток), а после этого – оценки для свободных клеток (тут (i;j) – адреса свободных клеток) – см. п.2.3.
4) При, в то время, когда все оценки , опорный замысел есть оптимальным, и остается определить значение целевой функции f(X1). В случае, если же среди оценок были хорошие, то выбираем ячейку с громаднейшей хорошей оценкой, строим для нее цикл и переходим к новому опорному ответу X2 – см. п. 2.4. Наряду с этим должно выполняться неравенство f(X2)? f(X1). После этого возвращаемся к п. 3) метода.
2.6. Задания для независимой работы.
Решить транспортные задачи (выяснить оптимальное значение целевой функции).
|
1) |
| В А | |||
2)
|
3) |
| В А | ||||
4)
5)
6)
7)

9)
10)
| В А | ||||
Практическое занятие №3