Машина Тьюринга (структура, такт работы, запись программы, правила исполнения программы, неприменимость и применимость метода к слову, соглашения для сокращения записи программы). Возможности МТ (композиция, повторение и разветвление МТ) Тезис Тьюринга.
Алгоритмически неразрешимые неприятности (определение алгоритмически разрешимых и неразрешимых задач, понятия записи метода и самоприменимости, теорема об алгоритмической неразрешимости неприятности самоприменимости)
Методы обрабатывают определённые объекты („входные) и выдают объекты („выходные) в качестве результатов. Объекты могу быть конкретными, как, к примеру, десятичное число при A. Объекты смогут быть абстрактными, как, скажем, натуральные числа (для которых смогут употребляться разнообразные эквивалентные совокупности представления) при B — для обрисованного в том месте метода совсем несущественно, записываются числа в десятичной либо бинарной совокупности счисления либо кроме того римскими цифрами, свойства делимости от этого не изменяются. В теоретических изучениях предпочитают опираться на методы, каковые трудятся, к примеру, лишь с натуральными числами (Гёдель), или лишь с цепочками знаков (Марков). С практической точки зрения нет ничего хорошего либо потребности в таких ограничениях, допустимы какие конкретно угодно множества объектов, в случае, если лишь возможно бережно выяснить их свойства. Разве только, потому, что приходится завлекать разбор отдельных случаев, нужно включить в множество объектов по крайней мере значения истинности «ложь» и «истина».
В зависимости от того, какие конкретно допускаются классы объектов (соответствующие операции), приходят к разным классам методов.
Методы Маркова
Исходя из сообщённого, возможно констатировать, что операционные правила обработки дискретных сообщений являются методами над последовательностями знаков. Приступим сейчас к уточнению понимавшегося до сих пор интуитивно понятию метода. В частности, нам предстоит узнать, что можно считать „элементарными тактами обработки.
Несомненно, элементарной операцией над последовательностями знаков может принимать во внимание замена подслова на некое слово (текстовая замена). Будем исходить из слов и множеств над неспециализированным комплектом знаков (это возможно делать без ограничения общности). Отдельную операцию замены (продукцию) будем записывать в виде и понимать ее так:
| Операция замены: «В случае, если а есть подсловом заданного слова х, то заменить это подслово на Ь. , если подслово а видится в слове х пара раз, словом Ь заменяется то из них, которое стоит в самой левой позиции». | (*) |
Потом, в случае, если дано (конечное) множество таких продукций, перечисленных в определённом порядке, то текстовая замена обязана производиться при помощи применения самой первой (довольно этого порядка) из применимых продукций. Все это повторяется до тех пор, покуда быть может, либо же до применения особенным образом отмеченной продукции („останавливающей).
Для того чтобы рода методы именуют методами Маркова по имени советского математика А. А. Маркова, что в первый раз обрисовал их (в 1951 г.); сам Марков именовал их „обычными алгорифмами. Методы Маркова вычисляют уточнением понятия метода, достигаемым за счёт применения особой формы описания.
Как пример приведем метод Маркова, что по заданному бинарному слову сооружает производное бинарное слово. Данный метод применяет вспомогательные символы ? „челноки и содержит следующие продукции:
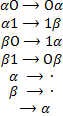
Останавливающие продукции отмечены точкой. На рисунке ниже продемонстрировано использование метода к слову 001101110101.
?001101110101
0?01101110101
00?1101110101
001?101110101
0010?01110101
00101?1110101
001011?110101
0010110?10101
00101100?0101
001011001?101
0010110011?01
00101100111?1
001011001111?
Благодаря компактным правилам замены методы Маркова являются замечательное средство описания: на сегодня нет таких методов над последовательностями знаков, для которых не существовало бы метода Маркова, делающего ту же самую обработку сообщений. Описания, сформулированные в виде методов Маркова, довольно часто оказываются очень маленькими по сравнению с другими, менее „рафинированными формами описания. Увидим, что элементарную для методов Маркова операцию замены (*) возможно кроме этого разглядывать как сложную, рекурсивно определяемую операцию над последовательностями знаков. Исходя из этого понятие элементарности в любой момент довольно.
В зависимости от информации, содержащейся в обрабатываемых сообщениях, довольно часто, напротив, разглядывают как элементарные такие такты обработки, каковые, фактически говоря, являются сложными. Основанием для этого может служить, к примеру, тот факт, что такие макротакты практически складываются из конечного числа обрисованных выше текстовых замен, причём их внутренняя структура несущественна для предпринимаемой обработки. Так обстоит дело, скажем, для сложения, вычитания, деления и умножения с остатком, при, в то время, когда сообщения представлены целыми числами в некоей цифровой форме записи. В остальном же несущественно, представлена последовательность руководств в виде диаграммы либо как-нибудь более схематично, равно как несущественно да и то, обрисованы отдельные такты обработки словесно либо заданы при помощи формул.
Фактически действия с числами в цифровой записи относятся, так, к классу методов над цепочками знаков. Тут в математике мы обнаруживаем исторические корни слова algorismo; еще Лейбниц сказал об „методе умножения.
А.А. Марковым был сформулирован принцип нормализации: любая вычислимая в интуитивном смысле функция вычислима посредством некоего обычного алгорифма.
Тренажеры (эмуляторы) тут:
http://kpolyakov.spb.ru/prog/nma.htm
http://cmcmsu.no-ip.info/1course/alg.schema.nam.htm