Лабораторная работа 4
Диапазоны
Массивы
Ответ совокупности линейных уравнений
Цель работы:
Взять устойчивые навыки применения диапазонов, массивов, методов решения и матричных операций совокупности линейных уравнений.
К р а т к а я с п р а в к а.
Диапазон (смежный) ? несколько ячеек объединенных оператором ( : ).
Пример.
A3:A6, E11:G20.
Диапазон (не смежный) ? несколько ячеек и(либо) смежных диапазонов объединенных оператором ( ; ).
Пример.
A8; M12:N20; D16:E18.
Диапазону возможно присвоено имя.
Массив ? смежный диапазон, что обрабатывается табличным процессором MS Excel как единое (неделимое) целое формулами массива. В формулах массив записывается кроме этого как диапазон, заключенный в { } скобки. Ввод формулы массива осуществляется одновременным нажатием комбинации клавиш Ctrl+Shift+Enter. Массиву возможно (рекомендуется) присвоено имя. Перед вводом формулы нужно предварительно выделить на странице расположение и количество ячеек, достаточные для размещения массива.
Несложные операции над массивами
F Умножение массива на число:
{=A1:B3*10}
F Сумма (разность) массивов с однообразным числом строк и столбцов:
{=A1:C3+E1:G3}
F Поэлементное произведение (деление) массивов с однообразным числом строк и столбцов:
{=A1:D4*G1:J4}
F Вычисление некоей функции от каждого элемента массива:
{=COS(A1:D5)}.
Матрица ? массив, прямоугольная таблица чисел (элементов). Матрица, имеющая одну строчок либо один столбец, именуется вектор.
Операции над матрицами
F Несложные операции над матрицами выполняются кроме этого как над массивами.
F Умножение матриц. Произведение матрицы А на матрицу В выяснено лишь в том случае, в то время, когда число столбцов матрицы А равно строчков матрицы В. В следствии умножения получается матрица АВ, у которой столько же строчков, сколько их в матрице А, и столько же столбцов, сколько их в матрице В. Для умножение матриц в MS Excel имеется функция АВ = {=МУМНОЖ(A;B)}.
Пример.
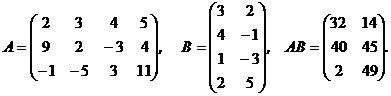
F Вычисление определителя матрицы (detA). Результатом есть число, которое занимает одну ячейку.
Аопр = {=МОПРЕД(А)}.
Потому, что результатом вычисления определителя есть одно число, то комбинацию клавиш Ctrl+Shift+Enter нажимать не обязательно.
F Вычисление обратной матрицы (А-1). Обратная матрица для того чтобы же размера, что и исходная.
Аобр = {=МОБР(А)}.
Свойство обратной матрицы
Произведение обратной матрицы и исходной равняется единичной матрицы.
Пример.
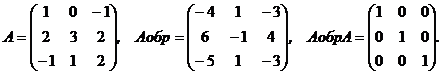
F Транспонирование матрицы. Транспонированной (АТ) к матрицы А есть матрица у которой число строчков равно столбцов матрицы А.
Атр = {=ТРАНСП(А)}.
Пример.
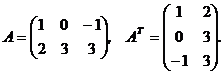
Задание 1
Используя матричные операции произвести действия над матрицами. Матрицам присвоить имена.
1. Даны две настоящие матрицы
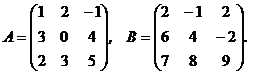
взять следующие матрицы:
А3; А2В; А2В-В; (А-В)2; (АВ)3; А3В+В2А.
2. Вычислить определитель матриц:
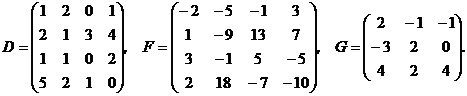
3. Определить значение формы Z = YTX2XTY в случае, если:
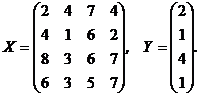
Задание 2
Решить совокупность уравнений способами: обратной матрицы и по формулам Крамера. Сделать диагностику ответа. Совокупности уравнений задания находятся в папке Лабораторная работа 7 файл Задание 2.doc.
Методика исполнения задания
В общем случае ответ совокупности линейных уравнений
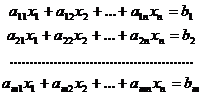имеет форму Х = А-1В, где А ? матрица коэффициентов аij,, В ? вектор-столбец свободных участников, Х ? вектор-столбец малоизвестных, А-1 ? матрица, обратная к матрице А.
Пример
Решить совокупность уравнений:
2Х1 ? Х2 + Х3 = 3
3Х1 + Х2 ? Х3 = 2
1. Ответ совокупности уравнений способом обратной матрицы:
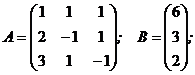Аобр = {=МОБР(А)} =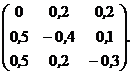 
X = {=МУМНОЖ(Аобр; В)} = Проверка А*Х = В.
Ответ по формулам Крамера.
Создаем вспомогательные матрицы А1, А2 и А3 заменой соответствующих столбцов матрицы А вектором-столбцом В:
А1 =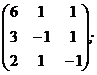 
А2 = 
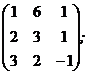А3 =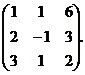 
Вычисляем определитель матрицы А:
D = {=МОПРЕД(А)} = 10.
Вычисляем определители запасных матриц:
D1 = {=МОПРЕД(А1)} = 10;
D2 = {=МОПРЕД(А2)} = 20;
D3 = {=МОПРЕД(А3)} = 30.
Вычисляем малоизвестные:
Х1 = D1/D = 1;
X2 = D2/D = 2;
X3 = D3/D = 3.
Методика ответа совокупности линейных уравнений способом обратной матрицы и по формулам Крамера приведена в файле Ответ совокупности уравнений.doc (папка Лабораторная работа 5).
Контрольные вопросы
1. Назовите числовые характеристики, которыми может описываться выборка. Приведите их формулы принятые в MS Excel.
2. Как в формулу вводится встроенная функция?
3. В чем отличие диапазона ячеек от массива?
4. Как присвоить имя диапазону, массиву?
5. Что нужно сделать на рабочем странице перед вводом массива?
6. Как осуществляется ввод формулы массива?
7. Как завершается ввод при комплекте формулы для работы с массивом ячеек?
8. Напишите формулу поэлементного произведения массивов.
9. В чем содержится последовательность действий при работе с массивами?
10. Какие конкретно существуют встроенные функции для работы с массивами?
11. Как выглядит формула, содержащая массивы, в строчке формул?
12. Объясните правило умножения матриц.
13. Какая матричная операция именуется транспонированной?