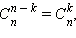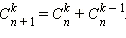Задачу возможно назвать комбинаторной, в случае, если ее ответом есть перебор элементов некоего конечного множества.
Особенная примета комбинаторных задач – вопрос, что возможно сформулировать так, что он начинался бы словами:
• какое количество методами…?
• какое количество вариантов…?
Чтобы решить задачу по комбинаторике, нужно сперва осознать её суть, другими словами, представить в мыслях процесс либо воздействие, обрисованное в задаче.
Необходимо чётко выяснить тип соединений в задаче, а для этого нужно, составив пара разных комбинаций, проверить повторяются ли элементы, изменяется ли их состав, серьёзен ли порядок элементов.
Пример 3
Встретились 6 друзей, и любой пожал руку каждому. какое количество всего было рукопожатий?
Продемонстрировать ответ
Любой пожал руку каждому, другими словами любой человек сделал 5 рукопожатий. Но общее число рукопожатий получается по правилу суммы: n 1 + n 2 + … + n 6 = 6 ? 5 = 30. Учтём сейчас то, что каждое рукопожатие мы посчитали два раза, и возьмём в следствии 15 рукопожатий.
Ответ. 15 рукопожатий.
Размещения
Пускай задано некое конечное множество из n разных элементов. Пускай из его элементов выбраны k разных штук ( k ? n ), тогда говорят, что произведена выборка количества k . В случае, если ответствен порядок, в котором произведена выборка элементов, то говорят об упорядоченной выборке , в случае, если порядок не серьёзен, то о неупорядоченной .
Упорядоченная выборка количества k из множества, складывающегося из n элементов, ( k ? n ) именуется размещением из n элементов по k . Количество размещений обозначается
Знак читается «а из эн по ка».
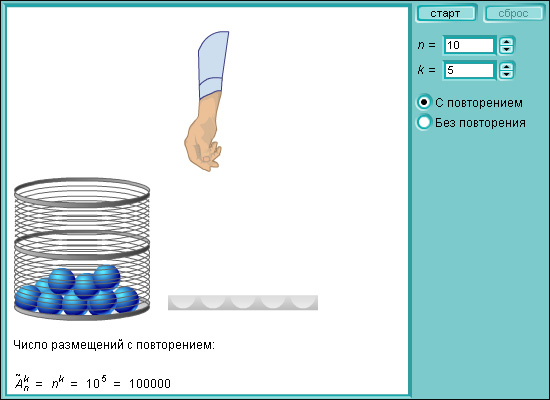
Модель 4.3. Размещения
Размещение из n элементов по n именуется перестановкой из n элементов . Количество перестановок обозначается P n .
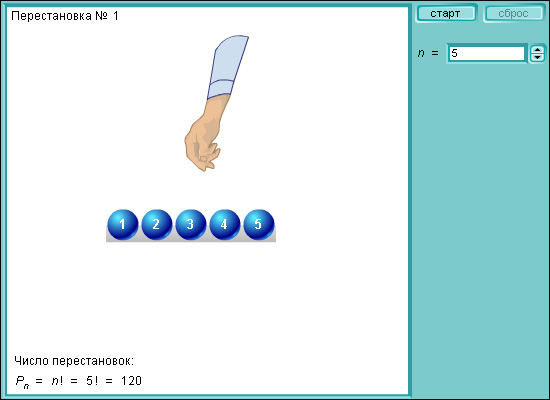
Модель 4.2. Перестановки
Иначе говоря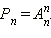 
Выведем формулу для числа Первый элемент выборки возможно выбрать n разными методами, второй – n ? 1 методом, …, направляться -й ? n ? ( k ? 1) методом. Значит, k элементов возможно выбрать
методами. В частности, P n = n · ( n – 1) · … · 2 · 1.
Введём следующее обозначение: n ! = n · ( n – 1) · … · 2 · 1. Знак «!» именуется знаком факториала либо легко факториалом . По определению считается, что 0! = 1. Посредством факториала возможно компактно записать выражение для и
Количество размещений из n элементов по k :
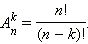
В частности, количество перестановок из n элементов:
P n = n !.
Пример 1
Вычислить
Продемонстрировать ответ
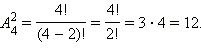
Ответ. 12.
Вычислять факториалы от солидных чисел не весьма комфортно. Для громадных n возможно применять оценочную формулу, предложенную шотландским математиком Джеймсом Стирлингом.
При громадных n выражение n ! возможно приближенно вычислить по формуле:
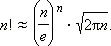
Буквой e тут, как в большинстве случаев, обозначено основание натурального логарифма e = 2,71828… При n = 10 погрешность при вычислении факториала посредством данной формулы образовывает менее 1 %, а при n = 100 – меньше 1/10 процента.
Возвратимся к формуле 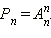Из неё направляться, что 
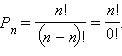В аналогичных обстановках считают, что 0! = 1, и это логично: единственный метод переставить 0 объектов – это ничего не делать.
Пример 2
какое количество семизначных чисел, кратных 5, возможно составить из цифр при условии, что цифры в записи числа не повторяются?
Продемонстрировать ответ
Последняя цифра искомого числа должна быть 0 либо 5. В первом случае остальные шесть цифр возможно выбирать из множества {1, 2, 3, …, 9}, и число вариантов равняется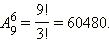 
Пускай сейчас число оканчивается цифрой 5. Тогда в качестве первой цифры возможно забрать любую из цифр 1, 2, 3, 4, 6, 7, 8, 9. Цифры со второй по шестую возможно выбрать 
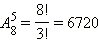методами. Значит, всего таких семизначных цифр существует
Ответ. 114240.
В прошлом примере цифры в числе не должны были повторяться. не меньше довольно часто, но, видятся задачи, в которых элементы в выборке смогут повторяться. Подобные выборки именуются размещениями с повторениями и обозначаются
Отыщем число На первое место возможно выбрать элемент n методами, на второе – кроме этого n методами, и без того потом. В случае, если количество мест равняется k , то по правилу количество разных выборок равняется
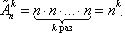
Количество размещений с повторениями обозначается знаком и вычисляется по формуле
Пример 3
какое количество разных пятибуквенных «слов» возможно составить из 26 букв латинского алфавита?
Продемонстрировать ответ
По формуле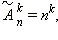 
где n = 26, k = 5, приобретаем: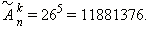 
Пример 4
У Васи имеется две однообразных копейки, один десятицентовик, три однообразных пенса и три однообразных лиры. какое количество методами Вася может разместить монеты в собственном альбоме, в случае, если количество мест в альбоме в точности равняется количеству монет?
1
Продемонстрировать ответ
При расстановке монет в альбоме серьёзен порядок следования монет – значит, речь заходит о количестве перестановок. Всего монет 9, и общее число перестановок равняется 9!. Но в случае, если мы переставим местами две однообразных копейки, то комплект от этого не изменится. Значит, ответ необходимо поделить на 2. Совершенно верно так же не изменится комплект и в том случае, если переставить между собой пенсы либо лиры. Количество перестановок 3 пенсов равняется 3!, лир – кроме этого 3!. Десятицентовик у Васи всего один, и количество перестановок для него равняется 1!, но для завершённости формулы учтём и его. Итак, количество способов, которыми возможно расставить монеты в альбоме, равняется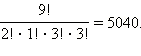 
Возможно сформулировать неспециализированное правило.
Количество перестановок из n элементов, среди которых имеется n 1 однообразных элементов первого сорта, n 2 однообразных элементов второго сорта, n k однообразных элементов k -го сорта, именуется числом перестановок с повторениями , обозначается знаком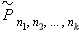 
и вычисляется по формуле
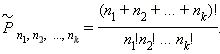
Сочетания
Допустим сейчас, что нас не интересует порядок, в котором идут выбранные элементы. К примеру, необходимо из десяти человек выбрать троих дежурных. Такая операция именуется неупорядоченной выборкой , либо сочетанием, в отличие от упорядоченной выборки – размещений.
Любая неупорядоченная выборка количества k из множества, складывающегося из n элементов, ( k ? n ) именуется сочетанием из n элементов по k . Количество сочетаний обозначается и вычисляется по формуле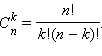 
Знак читается «це из эн по ка».
Формулу для возможно взять из следующих мыслей.
Из любого комплекта, содержащего k элементов, возможно взять k ! перестановок. Исходя из этого упорядоченных выборок количества k существует
штук. Значит,
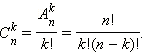
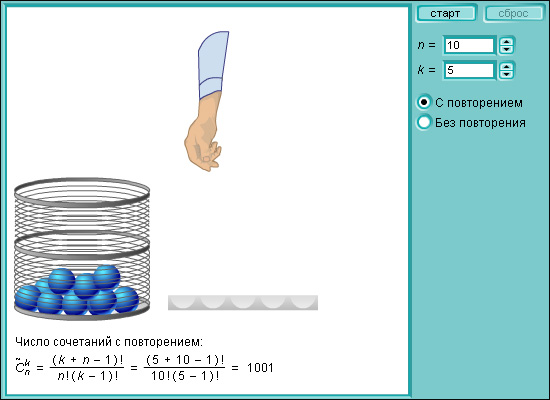
Модель 4.4. Сочетания
Пример 1
С целью проведения письменного экзамена необходимо составить 3 варианта по 5 задач в каждом. какое количество методами возможно разбить 15 задач на 3 варианта?
Продемонстрировать ответ
Задачи первого варианта возможно выбрать методами. Затем останется 10 задач, следовательно, второй вариант возможно составить методами. Для третьего варианта задачи возможно выбрать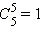 
методом. По правилу произведения приобретаем, что число способов равняется 
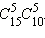Но нам всё равняется, какой вариант будет первым, какой – вторым, а какой – третьим. Потому отысканное число необходимо поделить на число перестановок из трёх элементов, другими словами на 3!. Совсем приобретаем, что число способов равняется 
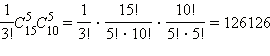способов.
Ответ. 126126.
Пример 2
какое количество методами возможно разместить 10 разных шаров по 4 коробкам так, дабы в первом коробке выяснилось 2 шара, во втором – 3, в третьем – 3 и в четвёртом опять два?
Продемонстрировать ответ
Пускай в первоначальный ящик попадет шаров, во второй – в третий – шаров, а в четвёртый – Тогда количество способов выборки в первоначальный ящик из n шаров определяется числом количество способов выборки во второй ящик шаров из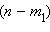 
оставшихся – числом 
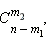для 4-го коробки – 
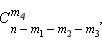а для k -го коробки то же число будет равняется 
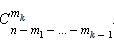Ответ найдётся по правилу произведения: 
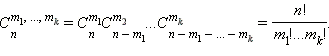В нашем случае
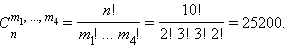
Для числа сочетаний честны кое-какие тождества, в частности:
Пример 3
Докажите тождество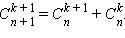 
Продемонстрировать ответ
Посредством формулы для приобретаем: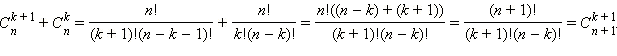 
Запишем в «нулевой» строчке число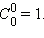 
В первой строке напишем значения чисел и каждое из которых также равняется 1, так, дабы значение выяснилось над промежутком между этими двумя числами. Во второй строке запишем числа и также равные 1, а между ними – число 
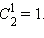Обратим внимание, что число равняется сумме двух чисел, стоящих над ним: 
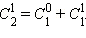Продолжим построение, записывая в n -й строке числа от до включительно.
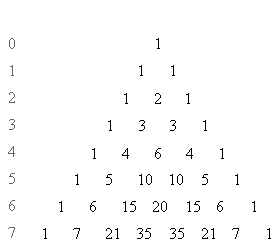1
Рисунок 4.2.3.1.
Полученный числовой треугольник именуется треугольником Паскаля . В соответствии с свойству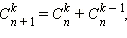 
любое число в этом треугольнике равняется сумме двух чисел, расположенных над ним в прошлой строчке.
При помощи треугольника Паскаля комфортно обосновывать разные комбинаторные тождества.
Пример 4
Доказать, что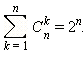 
Продемонстрировать ответ
Разглядим ( n + 1)-ю строчок треугольника Паскаля. Каждое число данной строки входит в качестве слагаемого в два соседних числа следующей строки. Так, сумма чисел очередной строки вдвое больше суммы чисел прошлой строки.
Эти числа образуют геометрическую прогрессию со знаменателем 2: 1, 2, 4, 8, 16 и без того потом. Наряду с этим сумма чисел в нулевой строчке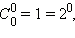 
в первой строке 
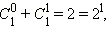во второй строке 
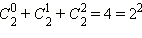и без того потом. Строгое подтверждение этого факта производится способом математической индукции.
Итак,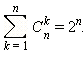
На языке множеств утверждение, доказанное в задаче, выглядит по-второму.
Число подмножеств множества из n элементов равняется 2 n .
Еще один интересный факт, который связан с треугольником Паскаля, мы приведём тут без доказательства:
Двучлен Ньютона
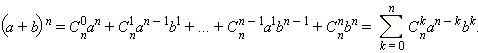
Приведённое тождество именуется двучленом Ньютона .
Как и при с размещениями, существует понятие числа сочетаний с повторениями. Разглядим его на следующем примере.
Пример 5
В палитре живописца 8 разных красок. Живописец берет кистью наугад любую из красок и ставит цветное пятно на ватмане. После этого берет следующую кисть, окунает её в любую из красок совершает второе пятно по соседству. какое количество разных комбинаций существует для шести пятен? Порядок пятен на ватмане не ответствен.
2
Продемонстрировать ответ
Решим задачу следующим образом. Пускай количество пятен первого цвета равняется k 1, второго цвета – k 2, третьего – k 3 и без того потом. Запишем каждое из этих чисел последовательностью из соответствующего количества единиц, а на границах между числами поставим нули. Так, в случае, если у нас первого цвета 1 пятно, второго – 3 пятна, третьего и четвёртого – ни одного, пятого и шестого – по одному пятну, а седьмого и восьмого – опять не одного, то запись будет выглядеть следующим образом: 1011100010100. В данной цепочке содержится m 1 = 6 единиц, m 0 – 1 = 8 – 1 = 7 нулей – всего n = m 0 + m 1 – 1 = 13 цифр. Количество перестановок с повторениями этих цифр равняется
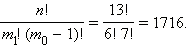Конкретно столько существует разных вариантов раскраски ватмана (без учёта порядка цветных пятен).
По большому счету, возможно сформулировать следующее правило.
В случае, если из множества, содержащего n элементов, выбирается поочередно m элементов, причём выбранный элемент любой раз возвращается обратно, то количество способов произвести неупорядоченную выборку – число сочетаний
Из истории комбинаторики Комбинаторика занимается разного вида соединениями, каковые возможно образовать из элементов конечного множества. Кое-какие элементы комбинаторики были известны в Индии еще во II в. до н. э. Индийцы умели вычислять числа, каковые на данный момент именуют сочетания. В XII в. Бхаскара вычислял кое-какие виды перестановок и сочетаний. Предполагают, что индийские ученые изучали соединения в связи с применением их в поэтике, науке о структуре стиха и поэтических произведениях. К примеру, в связи с подсчетом вероятных сочетаний ударных (продолжительных) и безударных (кратких) слогов стопы из n слогов. Как научная дисциплина, комбинаторика сформировалась в XVII в. В книге практика и Теория математики (1656 г.) французский создатель А. Кроме этого посвящает перестановкам и сочетаниям целую главу. Б. Паскаль в Трактате об арифметическом треугольнике и в Трактате о числовых порядках (1665 г.) изложил учение о биномиальных коэффициентах. П. Ферма знал о связях математических фигурных чисел и квадратов с теорией соединений. Термин комбинаторика начал употребляться по окончании опубликования Лейбницем в 1665 г. работы Рассуждение о комбинаторном мастерстве, в которой в первый раз дано научное обоснование перестановок и теории сочетаний. Изучением размещений в первый раз занимался Я. Бернулли во второй части собственной книги Ars conjectandi (мастерство предугадывания) в 1713 г. Современная символика сочетаний была предложена различными авторами учебных управлений лишь в XIX в. Все разнообразие комбинаторных формул возможно выведено из двух главных утверждений, касающихся конечных множеств – правило произведения и правило суммы. Правило суммы В случае, если конечные множества не пересекаются, то число элементов X U Y {либо} равняется сумме числа элементов множества X и числа элементов множества Y. Другими словами, в случае, если на первой полке стоит X книг, а на второй Y, то выбрать книгу из первой либо второй полки, возможно X+Y методами. Примеры задач Ученик обязан выполнить практическую работу по математике. Ему внесли предложение на выбор 17 тем по алгебре и 13 тем по геометрии. какое количество методами он может выбрать одну тему для практической работы? Ответ: X=17, Y=13 По правилу суммы X U Y=17+13=30 тем. Имеется 5 билетов финансово-вещевой лотереи, 6 билетов спортлото и 10 билетов автомотолотереи. какое количество методами возможно выбрать один билет из спортлото либо автомотолотереи? Ответ: Так как финансово-вещевая лотерея в выборе не участвует, то всего 6+10=16 вариантов. Правило произведения В случае, если элемент X возможно выбрать k методами, а элемент Y-m методами то несколько (X,Y) возможно выбрать k*m методами. Другими словами, в случае, если на первой полке стоит 5 книг, а на второй 10, то выбрать одну книгу с первой полки и одну со второй возможно 5*10=50 методами. Примеры задач Переплетчик обязан переплести 12 разных книг в красный, зеленый и коричневые переплеты. какое количество методами он может это сделать? Ответ: Имеется 12 книг и 3 цвета, значит по правилу произведения допустимо 12*3=36 вариантов переплета. какое количество существует пятизначных чисел, каковые одинаково читаются слева направо и справа налево? Ответ: В таких числах последняя цифра будет такая же, как и первая, а предпоследняя — как и вторая. Третья цифра будет любой. Это возможно представить в виде XYZYX, где Y и Z -любые цифры, а X — не ноль. Значит по правилу произведения количество цифр одинаково читающихся как слева направо, так и справа налево равняется 9*10*10=900 вариантов. Пересекающиеся множества Но не редкость, что множества X и Y пересекаются, тогда пользуются второй формулой. Примеры задач 20 человек знают британский и 10 — немецкий, из них 5 знают и английский язык , и германский. какое количество Человек всего? Ответ: 10+20-5=25 человек. Кроме этого довольно часто для наглядного ответа задачи используются круги Эйлера. К примеру: Из 100 туристов, отправляющихся в заграничное путешествие, германским языком обладают 30 человек, британским — 28, французским — 42. Британским и германским в один момент обладают 8 человек, британским и французским — 10, германским и французским — 5, всеми тремя языками — 3. какое количество туристов не обладают ни одним языком? Ответ: Выразим условие данной задачи графически. Обозначим кругом тех, кто знает английский язык , вторым кругом — тех, кто знает французский, и третьим кругом — тех, кто знают германский. Всеми тремя языками обладают три туриста, значит, в общей части кругов вписываем число 3. Британским и французским языком обладают 10 человек, а 3 из них обладают еще и германским. Следовательно, лишь британским и французским обладают 10-3=7 человек. Подобно приобретаем, что лишь британским и германским обладают 8-3=5 человек, а германским и французским 5-3=2 туриста. Вносим эти сведенья в соответствующие части. Определим сейчас, сколько человек обладают лишь одним из перечисленных языков. Германский знают 30 человек, но 5+3+2=10 из них обладают и другими языками, следовательно, лишь германский знают 20 человек. Подобно приобретаем, что одним британским обладают 13 человек, а одним французским — 30 человек. По условию задачи всего 100 туристов. 20+13+30+5+7+2+3=80 туристов знают хотя бы один язык, следовательно, 20 человек не обладают ни одним из данных языков. Размещения без повторений. какое количество возможно составить телефонных номеров из 6 цифр любой, так дабы все цифры были разны? Это пример задачи на размещение без повторений. Размещаются тут 10 цифр по 6. А варианты, при которых однообразные цифры стоят в различном порядке считаются различными. В случае, если X-множество, складывающиеся из n элементов, m?n, то размещением без повторений из n элементов множества X по m именуется упорядоченное множество X, содержащее m элементов именуется упорядоченное множество X, содержащее m элементов. Количество всех размещений из n элементов по m обозначают [pic] n! — n-факториал (factorial анг. сомножитель) произведение чисел натурального последовательности от 1 до какого именно или числа n n!=1*2*3*…*n 0!=1 Значит, ответ на вышепоставленную задачу будет [pic] Задача какое количество методами 4 парня смогут пригласить четырех из шести девушек на танец? Ответ: два юноши не смогут в один момент пригласить одну и ту же девушку. И варианты, при которых одинаковые девушки танцуют с различными парнями считаются, различными, исходя из этого: [pic] Допустимо 360 вариантов. Перестановки без повторений При n=m (см. размещения без повторений) из n элементов по m именуется перестановкой множества x. Количество всех перестановок из n элементов обозначают Pn. Pn=n! Вправду при n=m: [pic] Примеры задач какое количество разных шестизначных чисел возможно составить из цифр 0, 1, 2, 3, 4,5, в случае, если цифры в числе не повторяются? Ответ:1) Отыщем количество всех перестановок из этих цифр: P6=6!=7202) 0 не имеет возможности находиться впереди числа, исходя из этого от этого числа нужно забрать количество перестановок, при котором 0 стоит в первых рядах. А это P5=5!=120. P6-P5=720-120=600 Квартет Проказница Мартышка Осел, Козел, Да косолапый Мишка Затеяли играться квартет … Находись, братцы находись! – Кричит Мартышка, — погодите! Как музыке идти? Так как вы не так сидите… И без того, и этак пересаживались – снова музыка на лад не идет. Тут пуще прошлого пошли у низ раздоры И споры, Кому и как сидеть… Возможно, крыловские музыканты так и не перепробовали всех вероятных мест. Но способов не так уж и довольно много. какое количество? Тут идет перестановка из четырех, значит, допустимо P4=4!=24 варианта перестановок. Сочетания без повторений Сочетанием без повторений именуется такое размещение, при котором порядок следования элементов не имеет значения. Всякое подмножество X складывающееся из m элементов, именуется сочетанием из n элементов по m. Так, количество вариантов при сочетании будет меньше количества размещений. Число сочетаний из n элементов по m обозначается [pic]. [pic]. Примеры задач какое количество трехкнопочных комбинаций существует на кодовом замке (все три кнопки нажимаются в один момент), в случае, если на нем всего 10 цифр. Ответ: Так как кнопки нажимаются в один момент, то выбор этих трех кнопок – сочетание. Из этого допустимо [pic]вариантов. У одного человека 7 книг по математике, а у второго – 9. какое количество методами они смогут обменять приятель у приятеля две книги на две книги. Ответ: Так как нужно порядок следования книг не имеет значения, то выбор 2ух книг — сочетание. Первый человек может выбрать 2 книги [pic][pic] методами. Второй человек может выбрать 2 книги [pic]. Значит всего по правилу произведения допустимо 21*36=756 вариантов. При игре в домино 4 игрока дробят поровну 28 костей. какое количество методами они смогут это сделать? Первый игрок делает выбор из 28 костей. Второй из 28-7=21 костей, третий 14, а четвертый игрок забирает оставшиеся кости. Следовательно, допустимо [pic]. сочетания и Размещения с повторениями Довольно часто в задачах по комбинаторике видятся множества, в которых какие-либо компоненты повторяются. К примеру: в задачах на числа – цифры. Для таких задач при размещениях употребляется формула [pic], а для сочетаний [pic]. Примеры задач какое количество трехзначных чисел возможно составить из цифр 1, 2, 3, 4, 5? Ответ. Так как порядок цифр в числе значителен, цифры смогут повторяться, то это будут размещения с повторениями из пяти элементов по три, а их число равняется [pic]. В кондитерском магазине продавались 4 сорта пироженных: эклеры, песочные, наполеоны и слоеные. какое количество методами возможно приобрести 7 пироженных. Ответ: Приобретение не зависит от того, в каком порядке укладывают приобретённые пироженные в коробку. Приобретения будут разными, если они отличаются числом приобретённых пирожных хотя бы одного сорта. Следовательно, количество разных приобретений равно сочетаний четырех видов пироженных по семь — [pic]. Мартышку посадили за пишущую машинку с 45 клавишами, выяснить число попыток, нужных чтобы она точно напечатала первую строчок романа Л.Н. Толстого «Анна Каренина», в случае, если строчок содержит 52 повторений и знака не будет? Ответ: порядок букв имеет значение. Буквы смогут повторяться. Значит, всего имеется [pic] вариантов. Перестановки с повторениями [pic][pic], где n-количество всех элементов, n1,n2,…,nr-количество однообразных элементов. Примеры задач какое количество методами возможно переставить буквы слова «ананас»? Ответ: всего букв 6. Из них однообразны n1«а»=3, n2«н»=2, n3«с»=1. Следовательно, число разных перестановок равняется [pic]. Задачи для независимого ответа какое количество перестановок возможно сделать из букв слова «Миссисипи». Ответ: 2520 Имеется пять разных стульев и семь рулонов обивочной ткани разных цветов. какое количество методами возможно осуществить обивку стульев. Ответ: 16807 На памятные сувениры в «Поле Чудес» спонсоры предлагают кофеварки, утюги, телефонные аппараты, духи. какое количество методами 9 участников игры смогут взять эти сувениры? какое количество методами смогут быть выбраны 9 предметов для участников игры? Ответ: 49, 220 какое количество методами возможно расставить на шахматной доске 8 ладей так, дабы на одна из них не имела возможности бить другую? Ответ: 40320 какое количество возможно случая ручек 2 и выбора 3 карандашей из пяти разных карандашей и шести разных ручек? Ответ:200 какое количество способов раздачи карт на 4 человека существует в игре «Верю — не верю» (карты раздаются абсолютно, 36 карт). Ответ: [pic]. В течении 30 дней сентября было 12 дождливых дней, 8 ветреных, 4 холодных, 5 дождливых и ветреных, 3 дождливых и холодных, а один сутки был и дождливым, и ветреным, и холодным. В течение какое количество дней в сентябре стояла хорошая погода. Ответ: 15 На ферме имеется 20 свиньи и 24 овец. какое количество методами возможно выбрать одну свинью и одну овцу? В случае, если таковой выбор уже сделан, какое количество методами возможно сделать его еще раз? Ответ: 480, 437 какое количество методами возможно выбрать согласную и гласную буквы из слова «строение»? Ответ: 9 какое количество существует четных пятизначных чисел, начинающихся нечетной цифрой? Ответ: 25000 В книжный магазин поступили романы Ф. Купера «Прерия», «Зверобой», «Шпион», «Пионеры», «Следопыт» по однообразной цене. какое количество методами библиотека может закупить 17 книг на выбранный чек? Ответ:: 2985