Лекция № 3. Совокупности линейных уравнений.
Главные понятия.
Совокупностью линейных алгебраических уравнений, содержащей т уравнений и п малоизвестных, именуется совокупность вида:
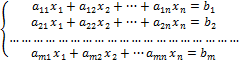
где числа аij ,i = 1,т , j =1,п именуются коэффициентами совокупности, числа bi – свободными участниками. Подлежат нахождению числа хп.
Такую совокупность комфортно записывать в компактной матричной форме А * Х = В.
Тут А – матрица коэффициентов совокупности, именуемая главной матрицей:
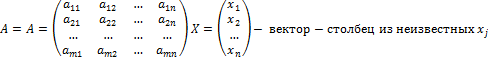
Произведение матриц А * Х выяснено, поскольку в матрице А столбцов столько же, сколько строчков в матрице Х (п штук).
Расширенной матрицей совокупности именуется матрица совокупности, дополненная столбцом свободных участников
Ответом совокупности называетсяп значений малоизвестных х1 = с1 , х2 = с2 , … , хп = сп, при подстановке которых все уравнения совокупности обращаются в верными равенства. Всякое ответ совокупности возможно записать в виде матрицы-столбца
Совокупность уравнений именуется совместной, если она имеет хотя бы одно ответ, и несовместимой, если она не имеет ни одного решения.
Ответ совокупностей линейных уравнений.
Ответ невырожденных линейных совокупностей (определитель не равен 0). Способ Крамера
Пускай имеется совокупность уравнений:
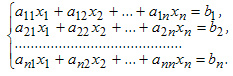
Обозначим через ? определитель матрицы совокупности и через ?j определитель, что получается из определителя ? заметой j-го столбца столбцом правых частей совокупности ( j=1,2,…n).
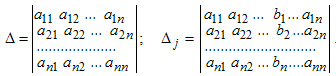
Теорема.
1.3.В случае, если определитель матрицы отличен от нуля, т.е. ? ?0, то совокупность имеет единственное ответ, которое находится по формуле: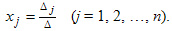 
Метод ответа совокупностей линейных алгебраических уравнений способом Крамера.
- Вычисляем определитель главной матрицы совокупности, убеждаемся, что он отличен от нуля.
- Находим определители ?j, каковые являются определителями матриц, взятых из матрицы А заменой k-ого столбца (k = 1, 2, …, n) на столбец свободных участников.
- Вычисляем искомые малоизвестные переменные x1, x2, …, xn по формулам.
- Делаем диагностику результатов, подставляя x1, x2, …, xn в исходную СЛАУ. Все уравнения совокупности должны обратиться в тождества. Возможно кроме этого вычислить произведение матриц A ? X, в случае, если в следствии оказалась матрица, равная B, то ответ совокупности отыскано правильно. В другом случае на протяжении ответа была допущена неточность.
Матричный метод (посредством обратной матрицы)
Пускай дана совокупность п линейных уравнений с п неизвестнымиили в матричной форме А * Х = В.
Отыщем ответ данной совокупности уравнений при ? ? 0.
Умножив обе части уравнения А * Х = В слева на матрицу А-1 , возьмём А-1 * А * Х = А-1 * В. Потому, что А-1 * А = Е и Е * Х = Х, то Х = А-1 * В.
Пример 4.3. Решить совокупность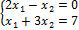 
Ответ:
Значит,
Задание 1. При помощи формул Крамера отыскать ответ совокупности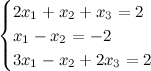 
Ответ. Вычисляем определитель матрицы совокупности:
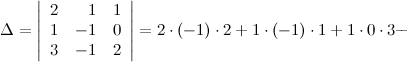
Так как определитель матрицы совокупности неравен нулю, то по теореме Крамера совокупность совместна и имеет единственное ответ. Для его нахождения вычислим следующие определители:
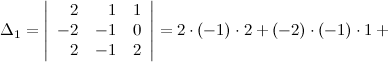
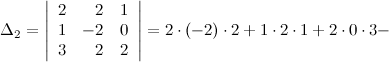
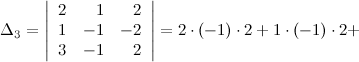
Так,
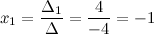
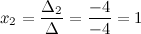
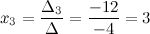
2) Отыщите ответ совокупности линейных уравнений способом Крамера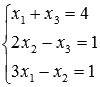 
. 
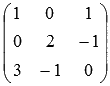
Ответ.
Перепишем совокупность в виде , дабы стало видно главную матрицу совокупности . Отыщем ее определитель по формуле
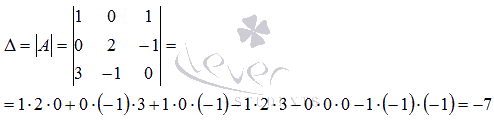
Определитель главной матрицы отличен от нуля, следовательно, совокупность линейных уравнений имеет единственное ответ. Отыщем его способом Крамера. Вычислим определители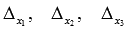 
:
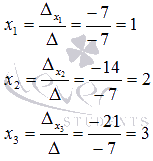
Ответ:
.
Обозначения малоизвестных переменных в уравнениях совокупности смогут различаться отx1, x2, …, xn. Это не воздействует на процесс ответа. А вот порядок следования малоизвестных переменных в уравнениях совокупности крайне важен при составлении главной необходимых определителей и матрицы способа Крамера. Поясним данный момент на примере.
3) Применяя способ Крамера, отыщите ответ совокупности трех линейных алгебраических уравнений с тремя малоизвестными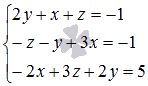 
.
Ответ. – Домашнее задание
В данном примере малоизвестные переменные имеют второе обозначение (x, y иz вместо x1, x2 и x3). Это не воздействует на ход ответа, но будьте внимательны с обозначениями переменных. В качестве главной матрицы совокупности Запрещено брать. Нужно сперва упорядочить малоизвестные переменные во всех уравнениях совокупности. Для этого перепишем совокупность уравнений как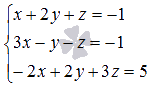 
. Сейчас главную матрицу совокупности отлично видно 
.
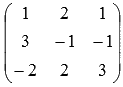Дополнительные примеры: