Разложению в ряд Фурье смогут подвергаться периодические сигналы. Наряду с этим они представляются в виде суммы гармонических функций, или комплексных экспонент с частотами, образующими арифметическую прогрессию. Чтобы такое разложение существовало, фрагмент сигнала длительностью в один период обязан удовлетворять условиям Дирихле:
1. Не должно быть разрывов второго рода (с уходящими в бесконечность ветвями функции).
2. Число разрывов первого рода (скачков) должно быть конечным.
3. Число экстремумов должно быть конечным.
Последовательность Фурье возможно применён для представления не только периодических сигналов, но и сигналов конечной длительности. Наряду с этим оговаривается временной промежуток, для которого строится последовательность Фурье, а в остальные моменты времени сигнал считается равным нулю. Для расчёта коэффициентов последовательности таковой подход практически свидетельствует периодическое продолжение сигнала за границами разглядываемого промежутка.
Способы Фурье употребляются для анализа линейных схем либо совокупностей: для предсказания реакции (отклика) совокупности; для определения передаточной функции; для оценки результатов тестов.
Произвольный периодический сигнал выражается через нескончаемое число гармоник с возрастающими частотами:
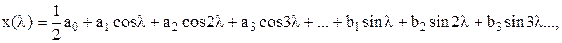
|
(2.7) | |||
| где | – | главные члены; | ||
| – | гармонические члены (при n 1, n – целое число); | |||
| – | коэффициенты гармоник; | |||
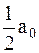
|
– | постоянный член либо составляющая постоянного тока. | ||
Период функции обязан равняться 2? либо кратной величине; помимо этого функция должна быть однозначной. Последовательность Фурье возможно разглядывать как «рецепт изготовление» любого периодического сигнала из синусоидальных составляющих. Дабы этот последовательность имел практическое значение, он обязан сходиться, т.е. частичные суммы последовательности должны иметь предел.
Процесс создания произвольного периодического сигнала из коэффициентов, обрисовывающих смешивание гармоник, именуется синтезом. Обратный процесс вычисления коэффициентов именуется анализом. Вычисление коэффициентов облегчается тем, что среднее от перекрёстных произведений синусоиды на косинусоиду (и напротив) равняется 0.
Введём в пространство Гильберта базис: Для упрощения будем считать, что он ортонормированный.
Тогда любую функцию из пространства Гильберта возможно представить через проекции вектора х на оси базиса обобщённым рядом Фурье:
| (2.8) | ||||
| где | – | коэффициент разложения в обобщённый последовательность Фурье. | ||
Последовательности Фурье особенно нужны при описании произвольных периодических сигналов с конечной энергией каждого периода. Помимо этого, они смогут употребляться для описания непериодических сигналов, имеющих конечную энергию за конечный промежуток. На практике для описания таких сигналов применяют интеграл Фурье.
Выводы
1. Для описания периодических сигналов активно используется последовательность Фурье. Для описания непериодических сигналов применяют интеграл Фурье.
Заключение
1. Сообщения, помехи и сигналы как векторы (точки) в линейном пространстве возможно обрисовать через комплект координат в заданном базисе.
2. Для ТЭС громаднейший интерес при отображении сигналов воображает n-мерное пространство Евклида , нескончаемое дискретное пространство и пространство Гильберта Хэмминга 2n. В этих пространствах вводится понятие скалярного произведения двух векторов (x,y).
3. Любую постоянную функцию времени как элемент возможно представить обобщенным рядом Фурье по заданному ортонормированному базису.
Литература
Главная:
1. Теория электрической связи: Учеб. Для институтов / А.Г. Зюко, Д. Д. Кловский, В.И. Коржик, М. В. Назаров; Под ред. Д. Д. Кловского. – М.: Радио и сообщение, 1998. – 433 с.
Дополнительная:
1. Прокис Дж. Цифровая сообщение: Пер. с англ. / Под ред. Д.Д. Кловского. – М.: Радио и сообщение, 2000. – 800 с.
2. Бернард Скляр. Цифровая сообщение. практическое применение и Теоретические основы: Пер. с англ. – М.: Издательский дом «Вильямс», 2003. – 1104 с.
3. Сухоруков А.С. Теория электрической связи: Конспект лекций. Часть 1. – М.:МТУСИ, ЦЕНТР ДО, 2002. – 65 с.
4. Сухоруков А.С. Теория цифровой связи: Учебное пособие. Часть 2. – М.:МТУСИ, 2008. – 53 с.
Создал:
| кандидат технических наук |
| О.Р. Кивчун |
| «___»__________ 2012 года |