Лабораторная работа №1.
Сплайны первого порядка.
ЗАДАНИЕ
Задать самостоятельно функцию у = f(x). Составить таблицу функции у = f(x) на отрезке [а;в] в узлах хi =a+ih. Вычислить промежуточные правильные значения посредством сплайна
1-порядка. Вычислить погрешность . Отыскать среднюю арифметическую величину (мат.ожидание)
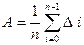
и среднеквадратическое отклонение
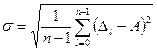 .
.
Методические указания
i. Задайте переменные программирования.
Массивы.
Переменные. Введем обозначения
M а= А, sig =? , x = x,i=i .
Константы. a, b, n, h, k
ii. Пример программы на языке Паскаль.
Пускай
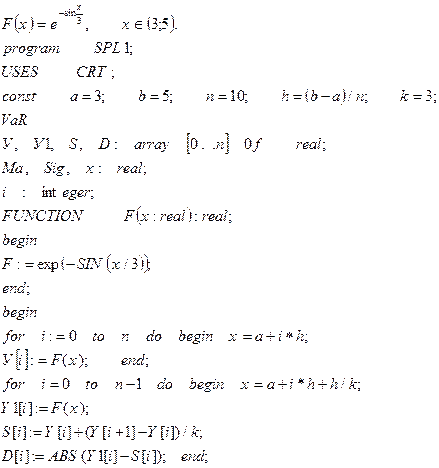
Ma : = O ; Sig : = O ;
For i : = O fo n-1 do
Ma : = Ma + D [i] /n ;
for семь дней : = O to n-1 do
Sig : = Sig + SQR (D [i] – Ma) / (n-1) ;
Sig : = SQRT (Sig);
WRITELN (’У = ’, ’ ’, ’У1= ’,’ ’, ’S = ’, ’, ’D =’);
For i : = O to n-1 do
WRITELN (У[i]:9:4,’ ’ , У1[i]:9:4, ’ ’ ,S[i]:9:4, ’ ’ , D[i]:9:4);
WRITELN (’ Ma ’, Ma, ’ ’, ’ Sig = ’, Sig) ;
end.
СРС №1.
Сплайны второго порядка.
Задание:
Забрать функцию у = f(x) из лабораторной работы №1. Составить таблицу функции у = f(x) на отрезке [а;в] в узлах хi =a+ih. Вычислить промежуточные правильные значения посредством сплайна
2-порядка. Вычислить погрешность . Отыскать среднюю арифметическую величину (мат.ожидание)
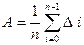
и среднеквадратическое отклонение
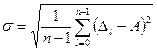 .
.
Результаты сравнить с лабораторной работой №1.
Методические указания
Расчетные формулы сплайна 2-го порядка.
1. Сперва вычисляются все коэффициенты .
2. Задается значение первой производной функций у=f (x) на левой границе отрезки [а,b], т.е. .
3. Из соотношения 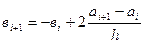 рекуррентно определяются все коэффициенты. .
рекуррентно определяются все коэффициенты. .
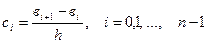 определяются все сi.
определяются все сi.
Переменные и структурная схема расчета.
Для составления программы вводятся следующие параметры расчета:
Массивы. — значения функций в целых узлах; значения функций в промежуточных узлах; коэффициенты сплайна 2-го порядка; значения сплайна в промежуточных точках;
отклонение;
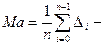 средняя арифметическая погрешность вычисления;
средняя арифметическая погрешность вычисления;
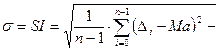 средне-квадратическое отклонение погрешности вычисления. Константы a, b, n, h=(b-a)/n; k; переменные Ma, SІ, х.
средне-квадратическое отклонение погрешности вычисления. Константы a, b, n, h=(b-a)/n; k; переменные Ma, SІ, х.
| начало |
Структурная схема расчета.
| а, в, n, k, f(x),b[0] |
— — — — — — — — — — — ввод начальных данных

I : = O, n, 1
| У[i] = f(x) |
I : = O, n-1, 1

I : = O, n-1, 1
| b[i+1]: = 2(У[i+1]- У[i]) / h-b[i] |
I : = O, n-1, 1
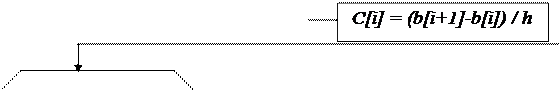 |
I : = O, n-1, 1
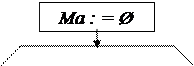 |
|||||
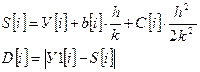
|
I : = O, n-1, 1
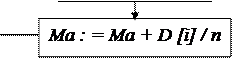 |
|||
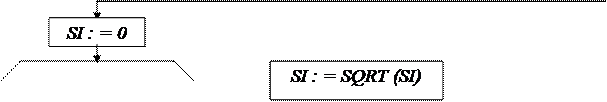 |
| финиш |
I : = O, n-1, 1
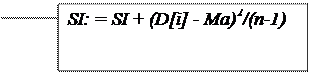
Лабораторная работа №2
Определение трансформации давления в пласте при упругом режиме (прямоугольный контур)
Постановка задачи.
| Задача 1. Между двумя параллельными сбросами находится нефтяная залежь 2 (рис.3), за пределами которой расположена вечно простирающаяся водоносная область. Стрелками продемонстрирован приток воды из законтурной области. Ширина залежи b=1000м, толщина пласта h=15м, проницаемость водоносной области к=0,2?10-12 м2, вязкость законтурной воды- , коэффициент пьезопроводности пласта . | 1у 1′ Ох в Рис.3 |
Отбор жидкости из залежи изменяется во времени следующим образом
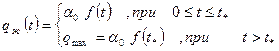
где t* – время ввода месторождения в разработку .
Требуется выяснить изменение давления на контуре нефтеносности
= P0– P(t), т.е. при у=0 (см. рис. 3) если сравнивать с начальным пластовым давлением по окончании начала разработки залежи.
Методические указания для ответа задачи 1.
Для расчета трансформации во времени давления на контуре нефтяной залежи применяя аппроксимацию Карслоу и Егеря [1] имеем:
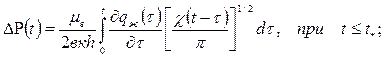
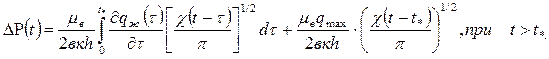
В лабораторной работе №2 нужно разработать программу для расчета падения давления на контуре прямоугольного пласта и нарисовать график функции . Наряду с этим , где постоянные c1, c2 выбираются студентами и согласуются с учителем.
Главные константы
Constmj=1/86400000 { }; k=2E-13 {k}; ka=86400 { }; b=1000; hh=15 {h}; h=25 {протяженность отрезка интегрирования по t, сут.}; tz=3*365 {t*=3 года}; tmax=15*365; n=trunc(tmax/h) {кол-во отрезков по t }; alfa=0.149 { };
Лабораторная работа №3.
Расчет показателей разработки нефтяного месторождения в законтурной области пласта при упругом режиме.
Постановка задачи.
 Задача 3. Для условий, данных в задаче 2 требуется выяснить изменение добычи нефти, воды, текущей обводненности и нефтеотдачи продукции при заданной динамике жидкости в течение 15 лет. Для разглядываемого месторождения известны эти зависимости (рис.3.1) текущей обводненности продукции от отношения Задача 3. Для условий, данных в задаче 2 требуется выяснить изменение добычи нефти, воды, текущей обводненности и нефтеотдачи продукции при заданной динамике жидкости в течение 15 лет. Для разглядываемого месторождения известны эти зависимости (рис.3.1) текущей обводненности продукции от отношения 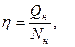 (Qн – накопленная добыча нефти, Nн – запасы нефти). Считается, что эта зависимость будет честной в течении (Qн – накопленная добыча нефти, Nн – запасы нефти). Считается, что эта зависимость будет честной в течении
|
0 0.5 |
разглядываемого срока разработки.
Методические указания
Главные константы
Constmv=1/86400000 { }; mn=2/86400000 { }; R=2000; hh=15 {h}; h=0.2 {ход по t, сут.}; tz=3*365 {t*=3 года}; tmax=15*365; n=trunc(tmax/h); a=1.0854; m=0.3; Scb=0.05;
V=pi*R*R*hh*m*(1-Scb); {Неспециализированный обьем нефти}
СРС №2.
Математическая модель.
Пускай протяженность стержня равна l м,
периметр поперечного сечения Р м,
площадь поперечного сечения Q м2.
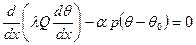 (4.1)
(4.1)
Пускай на обоих финишах стержня поддерживается постоянная температура . Тогда краевые условия имеют вид.
, (4.2)
Цель СРС №2.
— Разработать программу для расчета температуры на протяжении трубопровода , применяя трехточечную разностную схему (приближенное ответ);
— Изучить влияние длины трубы L, ?1 и ?2 , ? и ?0 на распределение температуры;
— направляться отыскать правильное ответ задачи (4.1)-(4.2). Для этого нужно решить дифференциальное ответ 2-порядка, считая ?=const. Правильное ответ нужно сравнить с приближенным ответом в узлах сетки и отыскать погрешность способа;
— Результаты представить на одном графике для сравнительного анализа.
Методические указания
Лабораторная работа №4
Независимая работа №3
Лабораторная работа № 5.
В лабораторной работе № 5 нужно вычислить значения кажущегося сопротивления и выстроить график в логарифмическом масштабе, применяя 3-точечный фильтр для установки Шлюмберже. Благодаря двукратному применению фильтра значения определяются в 6-ти точках на декаду логарифмического масштаба. Формула для расчета в логарифмическом масштабе
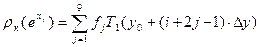 .
.
где 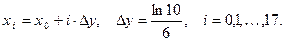
Коэффициенты фильтра 0,0148; -0,0814; 0,4018; -1,5716; 1,972; 0,1854; 0,1064; -0,0499; 0,0225.
Значения трансформанты сопротивления рассчитываются по соотношениям Пекериса.
Константы и переменные:nt=17; n=18; {число отсчетов}
R[1..10]; {удельные сопротивления}
T[1..nt]; {трансформанты сопротивления}
HS[1..9]; {мощности слоев}
x1, y, S, f, B: real; {х1- абсцисса первой точки измерения, у- текущая абсцисса, S – значение кажущегося сопротивления, f – ход, B – текущие значения трансформанты сопротивления }
i9, i8, i, j, m : integer; {i9- число слоев, i8=i9-1, i, j, m- счетчики}
Procedure TI (var B: real); {вычисляет текущие значения трансформанты сопротивления}
Блок-схема процедуры TI
 |
| B:=R[i9] |
| нет |
| да |

| a1:=exp(u); a2:=(a1-1/a1)/(a1+1/a1); B:=(B+a2*R[i])/(1+a2*B/R[i]) |
| i:=i9-k; u:=HS[i]/y |
 |
|||||
 |
|||||
| B:=R[i] |
Лабораторная работа №1.
Сплайны первого порядка.
ЗАДАНИЕ
Задать самостоятельно функцию у = f(x). Составить таблицу функции у = f(x) на отрезке [а;в] в узлах хi =a+ih. Вычислить промежуточные правильные значения посредством сплайна
1-порядка. Вычислить погрешность . Отыскать среднюю арифметическую величину (мат.ожидание)
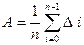
и среднеквадратическое отклонение
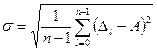 .
.
Методические указания
i. Задайте переменные программирования.
Массивы.
Переменные. Введем обозначения
M а= А, sig =? , x = x,i=i .
Константы. a, b, n, h, k
ii. Пример программы на языке Паскаль.
Пускай
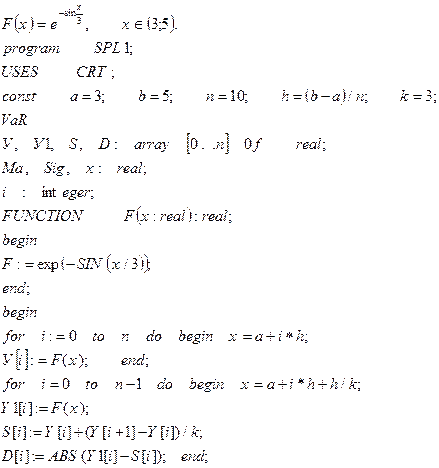
Ma : = O ; Sig : = O ;
For i : = O fo n-1 do
Ma : = Ma + D [i] /n ;
for i : = O to n-1 do
Sig : = Sig + SQR (D [i] – Ma) / (n-1) ;
Sig : = SQRT (Sig);
WRITELN (’У = ’, ’ ’, ’У1= ’,’ ’, ’S = ’, ’, ’D =’);
For i : = O to n-1 do
WRITELN (У[i]:9:4,’ ’ , У1[i]:9:4, ’ ’ ,S[i]:9:4, ’ ’ , D[i]:9:4);
WRITELN (’ Ma ’, Ma, ’ ’, ’ Sig = ’, Sig) ;
end.
СРС №1.
Сплайны второго порядка.
Задание:
Забрать функцию у = f(x) из лабораторной работы №1. Составить таблицу функции у = f(x) на отрезке [а;в] в узлах хi =a+ih. Вычислить промежуточные правильные значения посредством сплайна
2-порядка. Вычислить погрешность . Отыскать среднюю арифметическую величину (мат.ожидание)
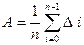
и среднеквадратическое отклонение
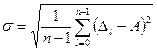 .
.
Результаты сравнить с лабораторной работой №1.
Методические указания
Расчетные формулы сплайна 2-го порядка.
1. Сперва вычисляются все коэффициенты .
2. Задается значение первой производной функций у=f (x) на левой границе отрезки [а,b], т.е. .
3. Из соотношения 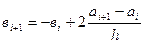 рекуррентно определяются все коэффициенты. .
рекуррентно определяются все коэффициенты. .
4. По формуле
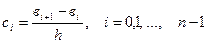 определяются все сi.
определяются все сi.